一问题描述

在森林里住着 N 只好斗的猴子。开始时，猴子们彼此不认识，难免吵架，吵架只发生在互不认识的两只猴子之间。吵架发生时，两只猴子都会邀请它们中最强壮的朋友来决斗。决斗过后，两只猴子和它们的所有朋友都认识对方，吵架不再发生。假设每只猴子都有一个强壮值，决斗后，强壮值会减少到原来的

一半（即10将减少到5，5将减少到2）；且每只猴子都认识自己，如果它是所有朋友中最强壮的，那么它自己也会去决斗。确定决斗后它们所有朋友的最大强壮值。

二输入和输出

1 输入

输入包含几个测试用例，每个测试用例都由两部分组成。第 1 部分的第 1 行包含一个整数 N（N≤10^5 ），表示猴子的数量；接下来的 N 行，每行都有一个数字，表示第 i 个猴子的强壮值 Vi（Vi≤32768）。第 2 部分的第 1 行包含一个整数 M（M≤10^5 ），表示发生了 M 次冲突；接下来的 M 行，每行都包含两个整数 x、y，表示第 x 个猴子和第 y 个猴子之间存在冲突。

2 输出

对每一次冲突，若两只猴子互相认识，则都输出 -1，否则输出决斗后它们所有朋友的最大强壮值。

三输入和输出样例

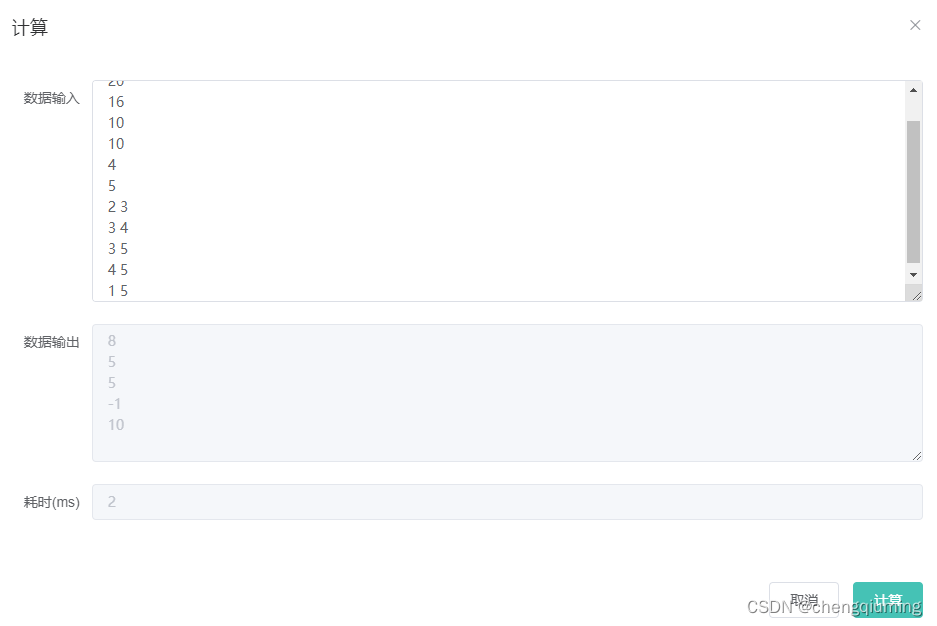
1 输入样例

5

20

16

10

10

4

5

2 3

3 4

3 5

4 5

1 5

2 输出样例

8

5

5

-1

10

四图解

根据输入样例1，初始状态如下图所示。

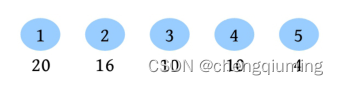
对输入样例的 5 种操作如下。

（1）2 3：猴子 2-3 决斗，强壮值减少一半，合并为一个群体，输出群体的最大强壮值 8。

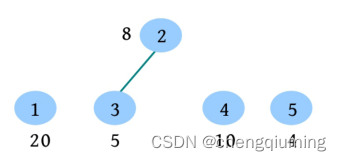
（2）3 4：猴子 3-4 冲突，3 所在群体的最强壮猴子 2 和 4 决斗，强壮值减少一半，合并为一个群体，输出群体的最大强壮值 5。

（3）3 5：猴子 3-5 冲突，3 所在群体的最强壮猴子 3 和 5 决斗，强壮值减少一半，合并为一个群体，输出群体的最大强壮值 5。

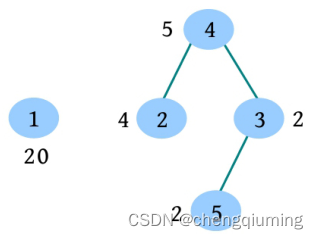
（4）4 5：猴子 4-5 冲突，4 和 5 猴子在一个群体，输出 -1。

（5）1 5：猴子 1-5 冲突，5 所在群体的最强壮猴子 4 和 1 决斗，强壮值减少一半，合并为一个群体，输出群体的最大强壮值 10。

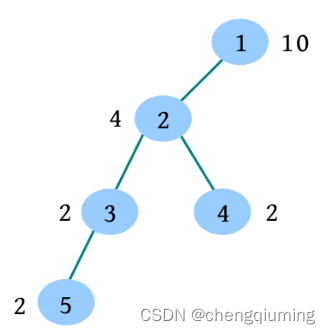
五分析和设计

1 分析

本问题是典型的堆合并问题，可使用左偏树（可合并堆）解决。

2 设计

（1）利用并查集记录群体的集合号。

（2）若猴子 x 、y 冲突，且两者的集合号相同（fx=fy），则输出 -1，否则：删除 x 所在堆的堆顶 fx，然后将 fx 的权值减少一半，合并到原来的堆中；删除 y 所在堆的堆顶 fy，然后将 fy 的权值减少一半，合并到原来的堆中；将上面两个堆合并，输出堆顶的值。

六代码

package com.platform.modules.alg.alglib.hdu1512;

public class Hdu1512 {
    public String output = "";
    private int maxn = 100010;

    int v[] = new int[maxn];
    int l[] = new int[maxn];
    int r[] = new int[maxn];
    int d[] = new int[maxn];
    int fa[] = new int[maxn];

    int merge(int x, int y) {
        if (x == 0) return y;
        if (y == 0) return x;
        if (v[x] < v[y]) {
            int temp = x;
            x = y;
            y = temp;

        }
        r[x] = merge(r[x], y);
        fa[r[x]] = x;
        if (d[l[x]] < d[r[x]]) {
            int temp = l[x];
            l[x] = r[x];
            r[x] = temp;
        }
        d[x] = d[r[x]] + 1;
        return x;
    }

    int find(int x) {
        if (fa[x] == x) {
            return x;
        } else {
            fa[x] = find(fa[x]);
            return fa[x];
        }
    }

    int pop(int x) {
        fa[l[x]] = l[x];
        fa[r[x]] = r[x];
        return merge(l[x], r[x]);
    }

    public String cal(String input) {
        int n, m, x, y;
        d[0] = -1;
        String[] line = input.split("\n");
        n = Integer.parseInt(line[0]);
        int count = 1;
        for (int i = 1; i <= n; i++) {
            v[i] = Integer.parseInt(line[count++]);
            l[i] = r[i] = d[i] = 0;
            fa[i] = i;
        }
        m = Integer.parseInt(line[count++]);

        while (m-- > 0) {
            String[] monkeys = line[count++].split(" ");
            x = Integer.parseInt(monkeys[0]);
            y = Integer.parseInt(monkeys[1]);

            int fx = find(x), fy = find(y);
            if (fx == fy) {
                output += "-1\n";
                continue;
            }
            int rt = pop(fx); // 删除最大值
            v[fx] /= 2;
            l[fx] = r[fx] = d[fx] = 0;
            fx = merge(rt, fx);
            rt = pop(fy);
            v[fy] /= 2;
            l[fy] = r[fy] = d[fy] = 0;
            fy = merge(rt, fy);
            rt = merge(fx, fy);
            output += String.format("%d\n", v[rt]);
        }

        return output;
    }
}