一、要实现的功能

如上图所示，在待处理的要素上右键单击，在弹出的右键列表中，点击【CC工具箱——处理要素空洞】按钮即可。

在弹出的工具框中，分别输入参数：

1、获取空洞，及获取要素边界。可多选

根据所选的处理模式，空洞和边界要素：

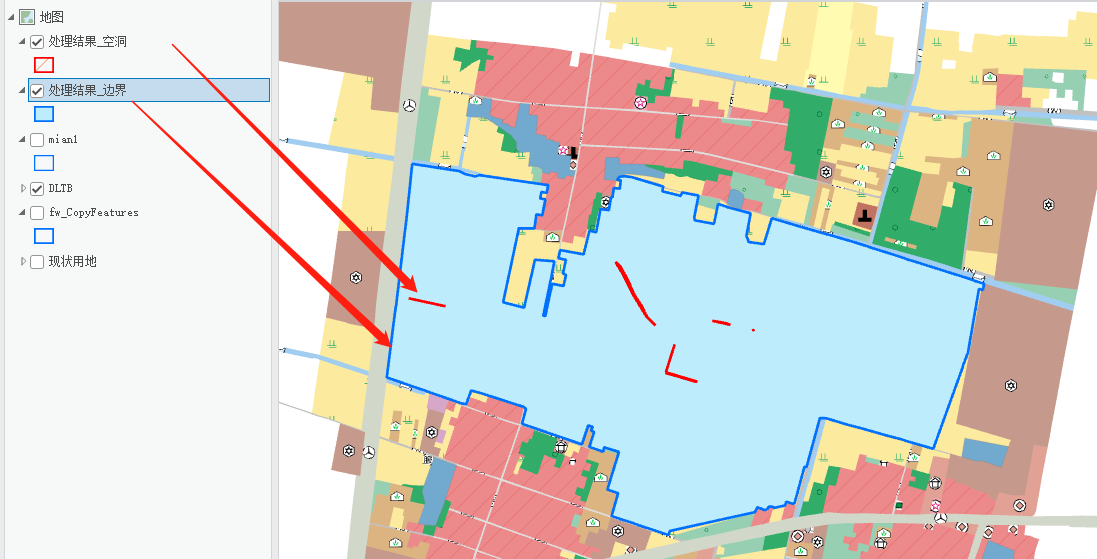
二、实现流程

工具其实就是调用了几个arcpy工具，组合一下即可。

这是主方法：

// 获取面空洞【输出模式：空洞 | 外边界】
public static void GetCave(string in_featureClass, string out_featureClass, string model = "空洞")
{
    // 获取默认数据库
    var gdb = Project.Current.DefaultGeodatabasePath;
    // 融合要素
    Arcpy.Dissolve(in_featureClass, gdb + @"\dissolve_fc");
    // 面转线
    Arcpy.PolygonToLine(gdb + @"\dissolve_fc", gdb + @"\dissolve_line");
    // 要素转面
    Arcpy.FeatureToPolygon(gdb + @"\dissolve_line", gdb + @"\dissolve_polygon");
    // 再融合，获取边界
    Arcpy.Dissolve(gdb + @"\dissolve_polygon", gdb + @"\dissolve_fin");
    // 擦除，获取空洞
    Arcpy.Erase(gdb + @"\dissolve_fin", gdb + @"\dissolve_fc", gdb + @"\single_fc");
    // 单部件转多部件，输出
    if (model == @"空洞")
    {
        Arcpy.MultipartToSinglepart(gdb + @"\single_fc", out_featureClass);
    }
    else if (model == @"外边界")
    {
        Arcpy.MultipartToSinglepart(gdb + @"\dissolve_fin", out_featureClass);
    }
    // 删除中间要素
    List<string> list_fc = new List<string>() { "dissolve_fc", "dissolve_line", "dissolve_polygon", "dissolve_fin", "single_fc" };
    foreach (var fc in list_fc)
    {
        Arcpy.Delect(gdb + @"\" + fc);
    }
}

调用一下即可：

// 获取默认数据库
var gdb = Project.Current.DefaultGeodatabasePath;
string output_extent = gdb + @"\处理结果_边界";
string output_cave = gdb + @"\处理结果_空洞";
// 获取输出模式
bool extent = (bool)check_getExtent.IsChecked;
bool cave = (bool)check_getCave.IsChecked;

await QueuedTask.Run(() =>
{
    if (extent)   // 获取边界
    {
        ToolManager.GetCave(ly.Name, output_extent, "外边界");
        ToolManager.AddFeatureLayerToMap(output_extent);
    }
    if (cave)   // 获取空洞
    {
        ToolManager.GetCave(ly.Name, output_cave);
        ToolManager.AddFeatureLayerToMap(output_cave);
    }
});