题目：

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

示例 1：

输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。

示例 2：

输入：nums = [0,1,0,3,2,3]
输出：4

示例 3：

输入：nums = [7,7,7,7,7,7,7]
输出：1

提示：

• 1 <= nums.length <= 2500
• -104 <= nums[i] <= 104

进阶：

• 你能将算法的时间复杂度降低到 O(n log(n)) 吗?

思路

首先通过本题大家要明确什么是子序列，“子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序”。

本题也是代码随想录中子序列问题的第一题，如果没接触过这种题目的话，本题还是很难的，甚至想暴力去搜索也不知道怎么搜。 子序列问题是动态规划解决的经典问题，当前下标i的递增子序列长度，其实和i之前的下表j的子序列长度有关系，那又是什么样的关系呢。

接下来，我们依然用动规五部曲来详细分析一波：

1. dp[i]的定义

本题中，正确定义dp数组的含义十分重要。

dp[i]表示i之前包括i的以nums[i]结尾的最长递增子序列的长度

为什么一定表示 “以nums[i]结尾的最长递增子序” ，因为我们在 做 递增比较的时候，如果比较 nums[j] 和 nums[i] 的大小，那么两个递增子序列一定分别以nums[j]为结尾 和 nums[i]为结尾， 要不然这个比较就没有意义了，不是尾部元素的比较那么 如何算递增呢。

1. 状态转移方程

位置i的最长升序子序列等于j从0到i-1各个位置的最长升序子序列 + 1 的最大值。

所以：if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);

注意这里不是要dp[i] 与 dp[j] + 1进行比较，而是我们要取dp[j] + 1的最大值。

1. dp[i]的初始化

每一个i，对应的dp[i]（即最长递增子序列）起始大小至少都是1.

1. 确定遍历顺序

dp[i] 是有0到i-1各个位置的最长递增子序列 推导而来，那么遍历i一定是从前向后遍历。

j其实就是遍历0到i-1，那么是从前到后，还是从后到前遍历都无所谓，只要吧 0 到 i-1 的元素都遍历了就行了。 所以默认习惯 从前向后遍历。

遍历i的循环在外层，遍历j则在内层，代码如下：

for (int i = 1; i < nums.size(); i++) {
    for (int j = 0; j < i; j++) {
        if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
    }
    if (dp[i] > result) result = dp[i]; // 取长的子序列
}

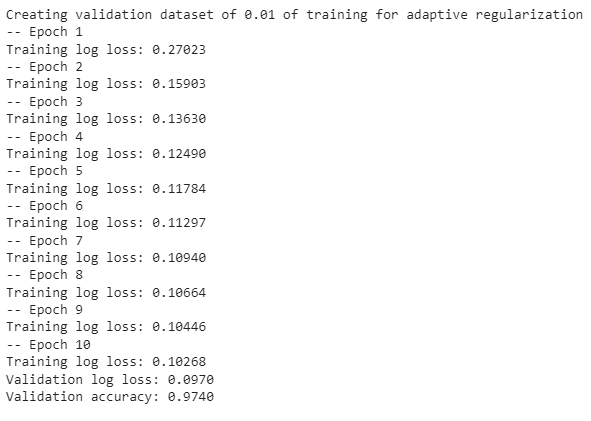
1. 举例推导dp数组

输入：[0,1,0,3,2]，dp数组的变化如下：

如果代码写出来，但一直AC不了，那么就把dp数组打印出来，看看对不对！

以上五部分析完毕，C++代码如下：

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        if (nums.size() <= 1) return nums.size();
        vector<int> dp(nums.size(), 1);
        int result = 0;
        for (int i = 1; i < nums.size(); i++) {
            for (int j = 0; j < i; j++) {
                if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
            }
            if (dp[i] > result) result = dp[i]; // 取长的子序列
        }
        return result;
    }
};

• 时间复杂度: O(n^2)
• 空间复杂度: O(n)

# 总结

本题最关键的是要想到dp[i]由哪些状态可以推出来，并取最大值，那么很自然就能想到递推公式：dp[i] = max(dp[i], dp[j] + 1);

子序列问题是动态规划的一个重要系列，本题算是入门题目，好戏刚刚开始！

二、力扣第674题：最长连续递增序列

题目：

给定一个未经排序的整数数组，找到最长且 连续递增的子序列，并返回该序列的长度。

连续递增的子序列 可以由两个下标 l 和 r（l < r）确定，如果对于每个 l <= i < r，都有 nums[i] < nums[i + 1] ，那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列。

示例 1：

输入：nums = [1,3,5,4,7]
输出：3
解释：最长连续递增序列是 [1,3,5], 长度为3。
尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的，因为 5 和 7 在原数组里被 4 隔开。 

示例 2：

输入：nums = [2,2,2,2,2]
输出：1
解释：最长连续递增序列是 [2], 长度为1。

提示：

• 1 <= nums.length <= 104
• -109 <= nums[i] <= 109

思路

本题相对于昨天的动态规划：300.最长递增子序列

(opens new window)最大的区别在于“连续”。

本题要求的是最长连续递增序列

# 动态规划

动规五部曲分析如下：

1. 确定dp数组（dp table）以及下标的含义

dp[i]：以下标i为结尾的连续递增的子序列长度为dp[i]。

注意这里的定义，一定是以下标i为结尾，并不是说一定以下标0为起始位置。

1. 确定递推公式

如果 nums[i] > nums[i - 1]，那么以 i 为结尾的连续递增的子序列长度 一定等于 以i - 1为结尾的连续递增的子序列长度 + 1 。

即：dp[i] = dp[i - 1] + 1;

注意这里就体现出和动态规划：300.最长递增子序列

(opens new window)的区别！

因为本题要求连续递增子序列，所以就只要比较nums[i]与nums[i - 1]，而不用去比较nums[j]与nums[i] （j是在0到i之间遍历）。

既然不用j了，那么也不用两层for循环，本题一层for循环就行，比较nums[i] 和 nums[i - 1]。

这里大家要好好体会一下！

1. dp数组如何初始化

以下标i为结尾的连续递增的子序列长度最少也应该是1，即就是nums[i]这一个元素。

所以dp[i]应该初始1;

1. 确定遍历顺序

从递推公式上可以看出， dp[i + 1]依赖dp[i]，所以一定是从前向后遍历。

本文在确定递推公式的时候也说明了为什么本题只需要一层for循环，代码如下：

for (int i = 1; i < nums.size(); i++) {
    if (nums[i] > nums[i - 1]) { // 连续记录
        dp[i] = dp[i - 1] + 1;
    }
}

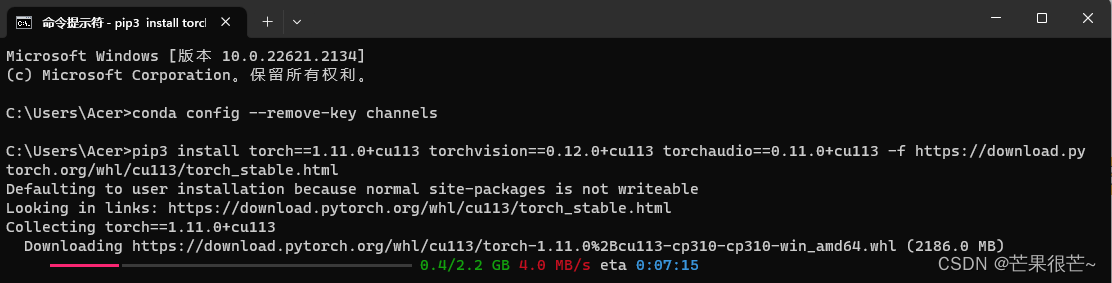
1. 举例推导dp数组

已输入nums = [1,3,5,4,7]为例，dp数组状态如下：

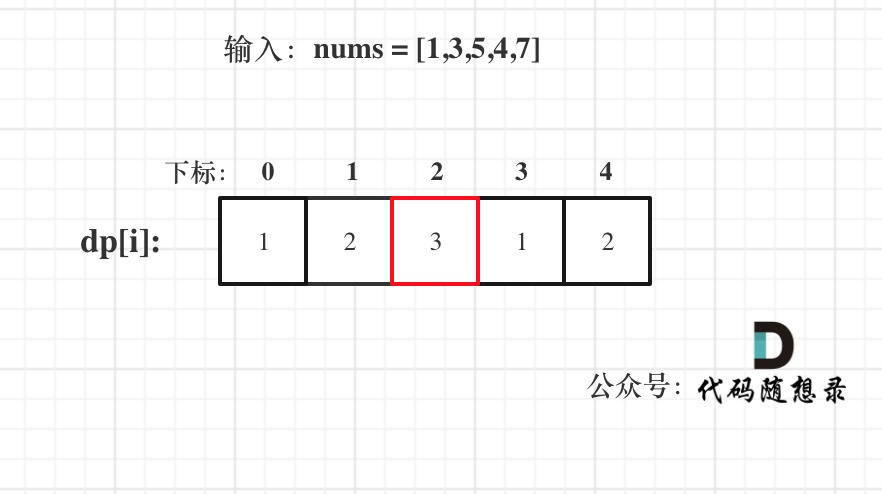
注意这里要取dp[i]里的最大值，所以dp[2]才是结果！

以上分析完毕，C++代码如下：

class Solution {
public:
    int findLengthOfLCIS(vector<int>& nums) {
        if (nums.size() == 0) return 0;
        int result = 1;
        vector<int> dp(nums.size() ,1);
        for (int i = 1; i < nums.size(); i++) {
            if (nums[i] > nums[i - 1]) { // 连续记录
                dp[i] = dp[i - 1] + 1;
            }
            if (dp[i] > result) result = dp[i];
        }
        return result;
    }
};

• 时间复杂度：O(n)
• 空间复杂度：O(n)

# 贪心

这道题目也可以用贪心来做，也就是遇到nums[i] > nums[i - 1]的情况，count就++，否则count为1，记录count的最大值就可以了。

代码如下：

class Solution {
public:
    int findLengthOfLCIS(vector<int>& nums) {
        if (nums.size() == 0) return 0;
        int result = 1; // 连续子序列最少也是1
        int count = 1;
        for (int i = 1; i < nums.size(); i++) {
            if (nums[i] > nums[i - 1]) { // 连续记录
                count++;
            } else { // 不连续，count从头开始
                count = 1;
            }
            if (count > result) result = count;
        }
        return result;
    }
};

• 时间复杂度：O(n)
• 空间复杂度：O(1)

# 总结

本题也是动规里子序列问题的经典题目，但也可以用贪心来做，大家也会发现贪心好像更简单一点，而且空间复杂度仅是O(1)。

在动规分析中，关键是要理解和动态规划：300.最长递增子序列

(opens new window)的区别。

要联动起来，才能理解递增子序列怎么求，递增连续子序列又要怎么求。

概括来说：不连续递增子序列的跟前0-i 个状态有关，连续递增的子序列只跟前一个状态有关

三、力扣第718题：最长重复子数组

题目：

给两个整数数组 nums1 和 nums2 ，返回 两个数组中 公共的 、长度最长的子数组的长度 。

示例 1：

输入：nums1 = [1,2,3,2,1], nums2 = [3,2,1,4,7]
输出：3
解释：长度最长的公共子数组是 [3,2,1] 。

示例 2：

输入：nums1 = [0,0,0,0,0], nums2 = [0,0,0,0,0]
输出：5

提示：

• 1 <= nums1.length, nums2.length <= 1000
• 0 <= nums1[i], nums2[i] <= 100

思路

注意题目中说的子数组，其实就是连续子序列。

要求两个数组中最长重复子数组，如果是暴力的解法 只需要先两层for循环确定两个数组起始位置，然后再来一个循环可以是for或者while，来从两个起始位置开始比较，取得重复子数组的长度。

本题其实是动规解决的经典题目，我们只要想到 用二维数组可以记录两个字符串的所有比较情况，这样就比较好推 递推公式了。 动规五部曲分析如下：

1. 确定dp数组（dp table）以及下标的含义

dp[i][j] ：以下标i - 1为结尾的A，和以下标j - 1为结尾的B，最长重复子数组长度为dp[i][j]。 （特别注意： “以下标i - 1为结尾的A” 标明一定是 以A[i-1]为结尾的字符串 ）

此时细心的同学应该发现，那dp[0][0]是什么含义呢？总不能是以下标-1为结尾的A数组吧。

其实dp[i][j]的定义也就决定着，我们在遍历dp[i][j]的时候i 和 j都要从1开始。

那有同学问了，我就定义dp[i][j]为 以下标i为结尾的A，和以下标j 为结尾的B，最长重复子数组长度。不行么？

行倒是行！ 但实现起来就麻烦一点，需要单独处理初始化部分，在本题解下面的拓展内容里，我给出了 第二种 dp数组的定义方式所对应的代码和讲解，大家比较一下就了解了。

1. 确定递推公式

根据dp[i][j]的定义，dp[i][j]的状态只能由dp[i - 1][j - 1]推导出来。

即当A[i - 1] 和B[j - 1]相等的时候，dp[i][j] = dp[i - 1][j - 1] + 1;

根据递推公式可以看出，遍历i 和 j 要从1开始！

1. dp数组如何初始化

根据dp[i][j]的定义，dp[i][0] 和dp[0][j]其实都是没有意义的！

但dp[i][0] 和dp[0][j]要初始值，因为 为了方便递归公式dp[i][j] = dp[i - 1][j - 1] + 1;

所以dp[i][0] 和dp[0][j]初始化为0。

举个例子A[0]如果和B[0]相同的话，dp[1][1] = dp[0][0] + 1，只有dp[0][0]初始为0，正好符合递推公式逐步累加起来。

1. 确定遍历顺序

外层for循环遍历A，内层for循环遍历B。

那又有同学问了，外层for循环遍历B，内层for循环遍历A。不行么？

也行，一样的，我这里就用外层for循环遍历A，内层for循环遍历B了。

同时题目要求长度最长的子数组的长度。所以在遍历的时候顺便把dp[i][j]的最大值记录下来。

代码如下：

for (int i = 1; i <= nums1.size(); i++) {
    for (int j = 1; j <= nums2.size(); j++) {
        if (nums1[i - 1] == nums2[j - 1]) {
            dp[i][j] = dp[i - 1][j - 1] + 1;
        }
        if (dp[i][j] > result) result = dp[i][j];
    }
}

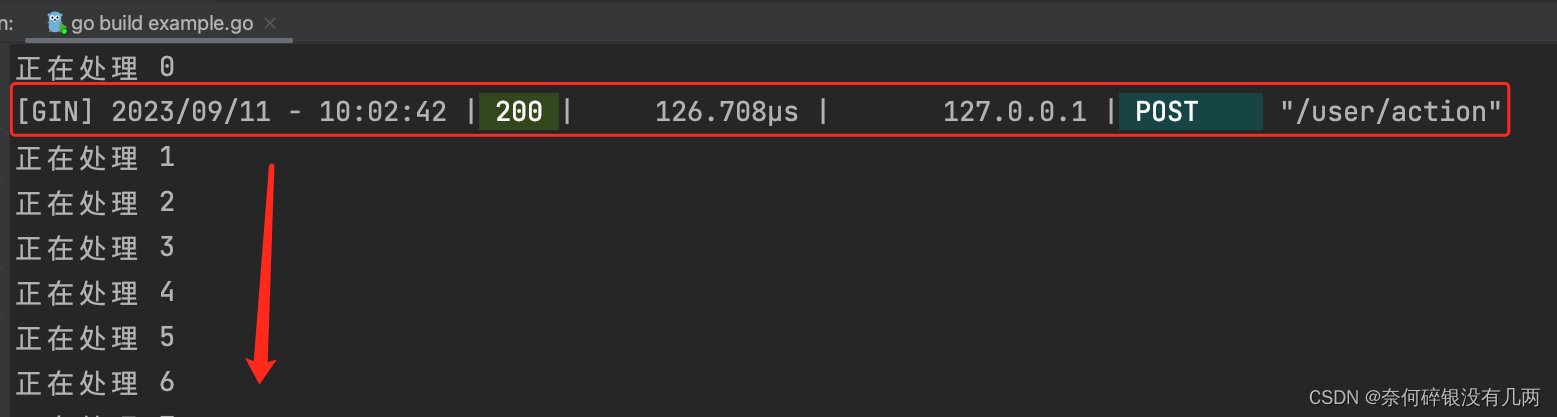
1. 举例推导dp数组

拿示例1中，A: [1,2,3,2,1]，B: [3,2,1,4,7]为例，画一个dp数组的状态变化，如下：

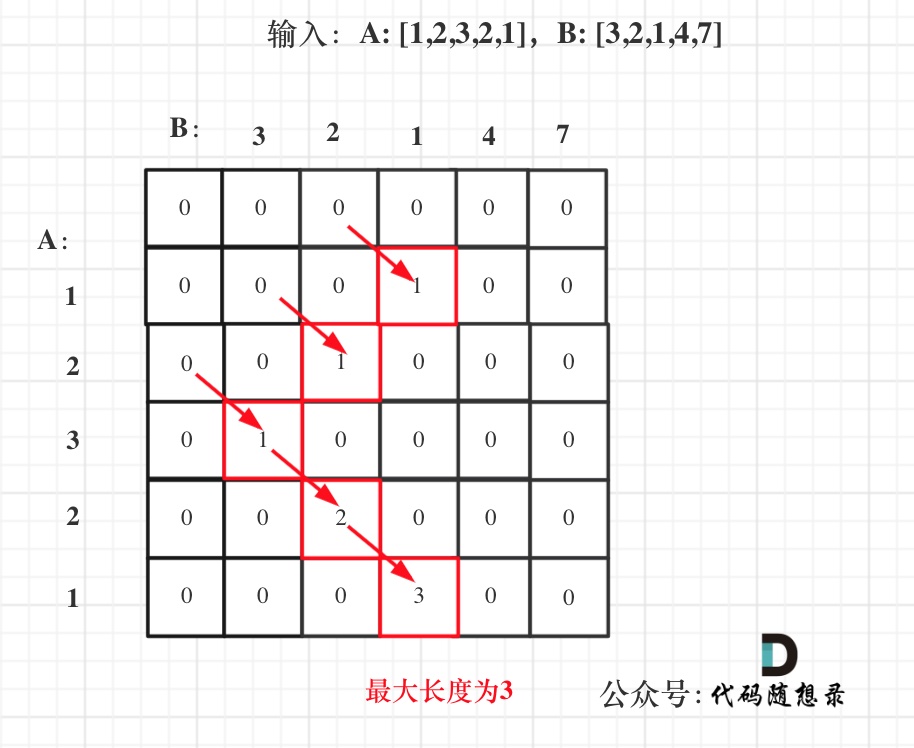
以上五部曲分析完毕，C++代码如下：

// 版本一
class Solution {
public:
    int findLength(vector<int>& nums1, vector<int>& nums2) {
        vector<vector<int>> dp (nums1.size() + 1, vector<int>(nums2.size() + 1, 0));
        int result = 0;
        for (int i = 1; i <= nums1.size(); i++) {
            for (int j = 1; j <= nums2.size(); j++) {
                if (nums1[i - 1] == nums2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }
                if (dp[i][j] > result) result = dp[i][j];
            }
        }
        return result;
    }
};

• 时间复杂度：O(n × m)，n 为A长度，m为B长度
• 空间复杂度：O(n × m)

# 滚动数组

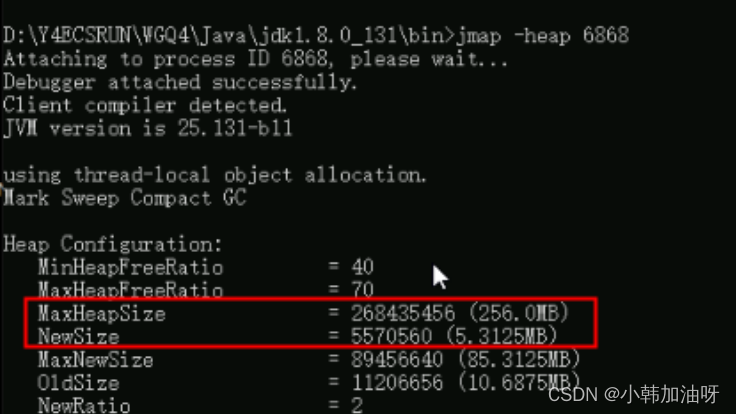
在如下图中：

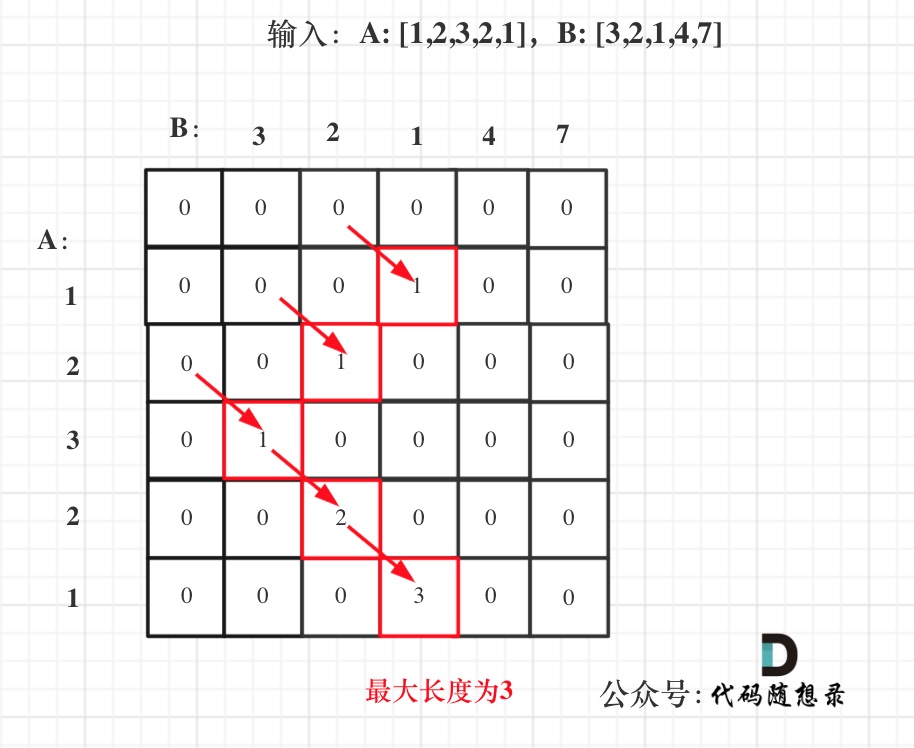
我们可以看出dp[i][j]都是由dp[i - 1][j - 1]推出。那么压缩为一维数组，也就是dp[j]都是由dp[j - 1]推出。

也就是相当于可以把上一层dp[i - 1][j]拷贝到下一层dp[i][j]来继续用。

此时遍历B数组的时候，就要从后向前遍历，这样避免重复覆盖。

// 版本二
class Solution {
public:
    int findLength(vector<int>& A, vector<int>& B) {
        vector<int> dp(vector<int>(B.size() + 1, 0));
        int result = 0;
        for (int i = 1; i <= A.size(); i++) {
            for (int j = B.size(); j > 0; j--) {
                if (A[i - 1] == B[j - 1]) {
                    dp[j] = dp[j - 1] + 1;
                } else dp[j] = 0; // 注意这里不相等的时候要有赋0的操作
                if (dp[j] > result) result = dp[j];
            }
        }
        return result;
    }
};

• 时间复杂度：$O(n × m)$，n 为A长度，m为B长度
• 空间复杂度：$O(m)$

# 拓展

前面讲了 dp数组为什么定义：以下标i - 1为结尾的A，和以下标j - 1为结尾的B，最长重复子数组长度为dp[i][j]。

我就定义dp[i][j]为 以下标i为结尾的A，和以下标j 为结尾的B，最长重复子数组长度。不行么？

当然可以，就是实现起来麻烦一些。

如果定义 dp[i][j]为 以下标i为结尾的A，和以下标j 为结尾的B，那么 第一行和第一列毕竟要进行初始化，如果nums1[i] 与 nums2[0] 相同的话，对应的 dp[i][0]就要初始为1， 因为此时最长重复子数组为1。 nums2[j] 与 nums1[0]相同的话，同理。

所以代码如下：

// 版本三
class Solution {
public:
    int findLength(vector<int>& nums1, vector<int>& nums2) {
        vector<vector<int>> dp (nums1.size() + 1, vector<int>(nums2.size() + 1, 0));
        int result = 0;

        // 要对第一行，第一列经行初始化
        for (int i = 0; i < nums1.size(); i++) if (nums1[i] == nums2[0]) dp[i][0] = 1;
        for (int j = 0; j < nums2.size(); j++) if (nums1[0] == nums2[j]) dp[0][j] = 1;

        for (int i = 0; i < nums1.size(); i++) {
            for (int j = 0; j < nums2.size(); j++) {
                if (nums1[i] == nums2[j] && i > 0 && j > 0) { // 防止 i-1 出现负数
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }
                if (dp[i][j] > result) result = dp[i][j];
            }
        }
        return result;
    }
};

大家会发现 这种写法 一定要多写一段初始化的过程。

而且为了让 if (dp[i][j] > result) result = dp[i][j]; 收集到全部结果，两层for训练一定从0开始遍历，这样需要加上 && i > 0 && j > 0的判断。

对于基础不牢的小白来说，在推导出转移方程后可能疑惑上述代码为什么要从i=0,j=0遍历而不是从i=1,j=1开始遍历，原因在于这里如果不是从i=0,j=0位置开始遍历，会漏掉如下样例结果：

nums1 = [70,39,25,40,7]
nums2 = [52,20,67,5,31]

当然，如果你愿意也可以使用如下代码，与上面那个c++是同一思路：

class Solution {
    public int findLength(int[] nums1, int[] nums2) {
        int len1 = nums1.length;
        int len2 = nums2.length;
        int[][] result = new int[len1][len2];

        int maxresult = Integer.MIN_VALUE;

        for(int i=0;i<len1;i++){
            if(nums1[i] == nums2[0])
                result[i][0] = 1;
            if(maxresult<result[i][0])
                    maxresult = result[i][0];
        }

        for(int j=0;j<len2;j++){
            if(nums1[0] == nums2[j])
                result[0][j] = 1;
            if(maxresult<result[0][j])
                maxresult = result[0][j];
        }

        for(int i=1;i<len1;i++){
            for(int j=1;j<len2;j++){

                if(nums1[i]==nums2[j])
                    result[i][j] = result[i-1][j-1]+1;

                if(maxresult<result[i][j])
                    maxresult = result[i][j];

            }

        }

        return maxresult;
    }
}

对于小白来说一定要明确dp数组中初始化的数据是什么

整体而言相对于版本一来说还是多写了不少代码。而且逻辑上也复杂了一些。 优势就是dp数组的定义，更直观一点。