差分的方法

差分实际上是前缀和的逆运算 ,这个关系和 积分与求导 的关系类似

例如有数组               ......    

和构造数组                 ......    

我们要使得a数组是b数组的前缀和       =       +    +    +  ......   +  

那么该如何构造b数组呢?    令  =     ,    =     -   ,     =     -   ,......    =    -   ,就可以得到b数组,那么我们就称 b数组是a数组的差分 ,其实这个构造方法不需要记忆,只要你 能够写出    =       +    +    +  ......   +  ,   -   就能够求出   

用处

当我们需要将[l,r]区间内的a数组都加上一个C时, 我们只需要对   加上一个C,那么  自然就加上了C,不过仅仅这样,会使得  并且后面的所有 a都加上C,但是我们的要求的区间是 [l,r] ,那么还需要将  减一个C,  并且后面的 a就不会受到影响,如下图

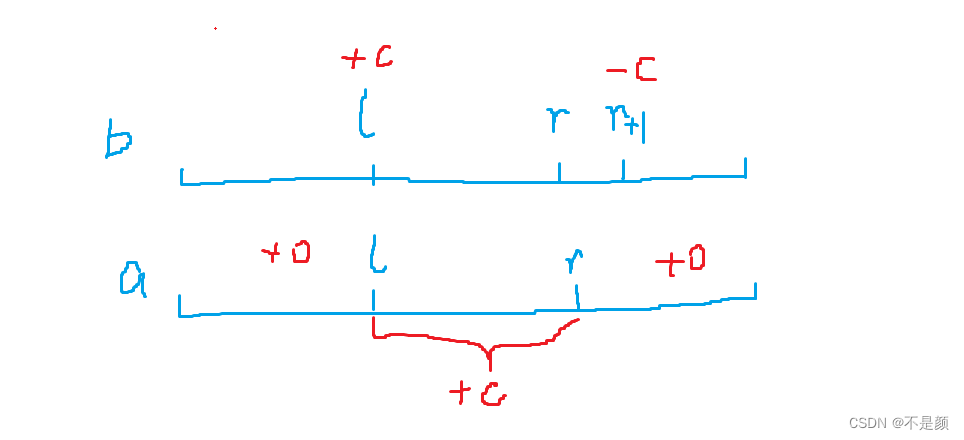
由于a数组是b数组的前缀和,所以 加C的影响 ,会从  开始 ,又因为后面  减去了一个C,所有 将加C的影响抵消会从  开始,所以 最后a数组中 [l,r] 区间内的数都加上了一个C

如果没有差分,我们要让区间内的数都加上一个C,我们要遍历这个区间,时间复杂度是O(n)

题目

题目
输入一个长度为n的整数序列。

接下来输入m个操作，每个操作包含三个整数l, r, c，表示将序列中[l, r]之间的每个数加上c。

请你输出进行完所有操作后的序列。

输入格式
第一行包含两个整数n和m。

第二行包含n个整数，表示整数序列。

接下来m行，每行包含三个整数l，r，c，表示一个操作。

输出格式
共一行，包含n个整数，表示最终序列。

数据范围
1 ≤ n , m ≤ 100000

1 ≤ l ≤ r ≤ n

− 1000 ≤ c ≤ 1000

− 1000 ≤ 整 数 序 列 中 元 素 的 值 ≤ 1000 

输入样例
 

6  3
1  2  2  1  2  1
1  3  1
3  5  1
1  6  1

输出样例
 

3  4  5  3  4  2

代码 

#include <iostream>

using namespace std;

const int N = 100010;
int a[N];
int b[N];
int n, m;


void insert(int l, int r, int c) 
{
	b[l] += c;
	b[r + 1] -= c;
}

int main(void)
{
	scanf("%d%d", &n, &m);

	for (int i = 1; i <= n; i++)
	{
		scanf("%d", &a[i]);
        b[i] = a[i] - a[i-1];

		//insert(i, i, a[i]); 
        //也可以这样写,因为你会发现b[i]也是等于a[i] - a[i-1]
        //所以可以使用insert()函数就不用花心思构造了
	}

	while (m--)
	{
		int l, r, c;
		scanf("%d%d%d", &l, &r, &c);
        
		insert(l, r, c);
	}


	for (int i = 1; i <= n; i++)
	{
		b[i] += b[i - 1]; //遍历,用b数组存储着b数组的前缀和
	}



	for (int i = 1; i <= n; i++)
	{
		printf("%d ", b[i]);
	}

}