软考备考-程序员-备考笔记
持续更新中》》》》》
更新日志：
刷题软件：
希赛网：每日一练和往年真题是免费的
软考通：完全免费
软考真题：完全免费
51CTO题库:微信小程序，不用下载，顺手
试卷题目情况
上午场均为选择题（题量70左右），下午场为大题（大题6道，内置多个选择和填空题）
知识点笔记（在考纲目录上拓展）：
一、计算机软件与软件工程基本知识(上午场)
1.1 计算机科学基础
1.1.1 数制及其转换
进位计数制
按进位的原则进行计数，称为进位计数制。
每一种进位计数制都有一组特定的数码，例如十进制有10个数码，二进制只有两个数码，而十六进制数却有16个数码。每一种进位计数制中允许使用的数码的总数称为基数或底数，对应地，十进制数的基数为10，二进制的基数为2，十六进制的基数则为16。
在任何一种进位计数制中，任何一个数都由整数和小数两部分组成，并且具有两种表示方式：位置计数法和多项式表示法。
例如：十进制数
100
（位置计数法）
=
1
∗
1
0
2
+
0
∗
1
0
1
+
0
∗
1
0
0
（多项式表示法）
例如： 十进制数100（位置计数法）=1*10^2+0*10^1+0*10^0（多项式表示法）
例如：十进制数100（位置计数法）=1∗102+0∗101+0∗100（多项式表示法）
进制
在采用进位计数的数字系统中，如果只用n个基本符号表示数值，则称其为n进制，n称为这个进制的基数。
下面是计算机中最常用的四种进制
二进制：是指在数学和数字电路中以2为基数的记数系统，二进制只有0和1两个数字符号，其运算规律是逢2进1，例如101101。为了与其他进制区别，二进制数的后缀都用大写字母B，例如101101B
八进制：一种以8为基数的计数法，采用0，1，2，3，4，5，6，7这八个数字符号，其运算规律是逢8进1，例如77。为了与其他进制区别，八进制数的后缀都用大写字母O（不是数字0），例如77O
十进制：一种以10为基数的计数法，采用0，1，2，3，4，5，6，7，8，9这十个数字符号，其运算规律是逢10进1，例如88。为了与其他进制区别，十进制数的后缀都用大写字母D，例如88D
十六进制：一种以16为基数的计数法，采用0，1，2，3，4，5，6，7，8，9，A，B，C，D，E，F这十六个数字和字母符号，其运算规律是逢16进1，例如9527。为了与其他进制区别，十六进制数的后缀都用大写字母H，例如9527H
| 进位制 | 二进制 | 八进制 | 十进制 | 十六进制 |
|---|---|---|---|---|
| 规则 | 逢二进一 | 逢八进一 | 逢十进一 | 逢十六进一 |
| 基数 | n=2 | n=8 | n=10 | n=16 |
| 数符 | 0,1 | 0,1,2,…,7 | 0,1,2,…,9 | 0,1,2,…,A,B,…,F |
| 权 | 2 x 2^x 2x | 8 x 8^x 8x | 1 0 x 10^x 10x | 1 6 x 16^x 16x |
| 形式标识符（后缀） | B | O | D | H |
进制转化
二进制转十进制：
按权展开法
二进制数0110 0100转化为十进制
01100100
（
2
）
=
2
7
×
0
+
2
6
×
1
+
2
5
×
1
+
2
4
×
0
+
2
3
×
0
+
2
2
×
1
+
2
1
×
0
+
2
0
×
0
=
100
（
10
）
0110 0100（2）= 2^7 \times 0+2^6 \times 1+2^5 \times 1+2^4 \times 0+2^3 \times 0+2^2 \times 1+2^1 \times 0+2^0 \times 0= 100（10）
01100100（2）=27×0+26×1+25×1+24×0+23×0+22×1+21×0+20×0=100（10）
小数部分的处理同理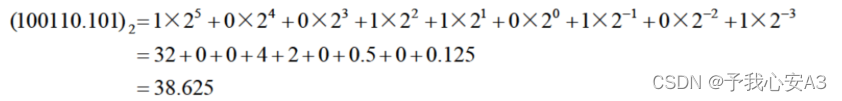
二进制转八进制：整数部分： 从低位往高位每三位一组，缺位处用0填补。这样每三位二进制数就对应一位八进制数小数部分：由高位向低位，每三位为一组，低位不足三位，在低位添“0”补足三位，这样每三位二进制数就对应一位八进制数。例：求（10010101.1011）(2)等值的八进制数
所以等值的八进制为(255.54)(8)
二进制转十六进制
整数部分： 从低位往高位每四位一组，缺位处用0填补。这样每四位二进制数就对应一位十六进制数
小数部分：则由高位向低位，每四位为一组，低位不足四位，在低位添“0”补足四位，这样每四位二进制数就对应一位十六进制数。
例：将（11110010001.11011）(2)转化为等值是十六进制数
所以对应16进制为791.D8
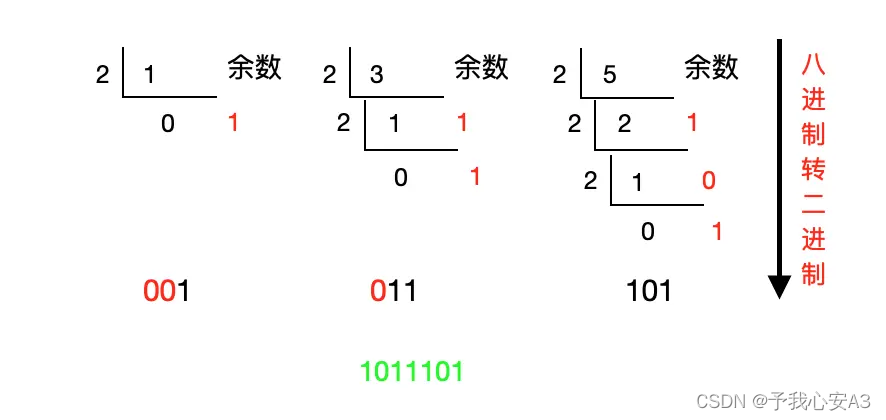
八进制转二进制
每一位八进制数对应三位二进制数，转化后的二进制数去掉整数部分高位的“0”和小数部分低位的“0”得结果。
标准做法：
八进制数 135 转成二进制为 1011101
快捷做法
可以用421辅助计算每一位8进制的二进制，其中4,2,1是二进制的权值。
如八进制的7可以用4+2+1得到，也就是111(2)，
2
2
×
1
+
2
1
×
1
+
2
0
×
1
=
7
2^2 \times 1+2^1 \times 1+2^0 \times 1=7
22×1+21×1+20×1=7
八进制的5可以用4+0+1得到，也就是101(2)
2
2
×
1
+
2
1
×
0
+
2
0
×
1
=
5
2^2 \times 1+2^1 \times 0+2^0 \times 1=5
22×1+21×0+20×1=5
八进制转十进制
按权展开，即将八进制每位上的数乘以位权，然后相加之和即是十进制数
1234 ( 8 ） = 1 × 8 3 + 2 × 8 2 + 3 × 8 1 + 4 × 8 0 = 668 ( 10 ） 1234(8）= 1 \times 8^3+2\times8^2+3\times8^1+4\times8^0=668(10） 1234(8）=1×83+2×82+3×81+4×80=668(10）
八进制转十六进制
先把八进制转成二进制后再转为十六进制
十进制转二进制
除2取余，倒序输出，小数采用“乘2取整”，顺序输出
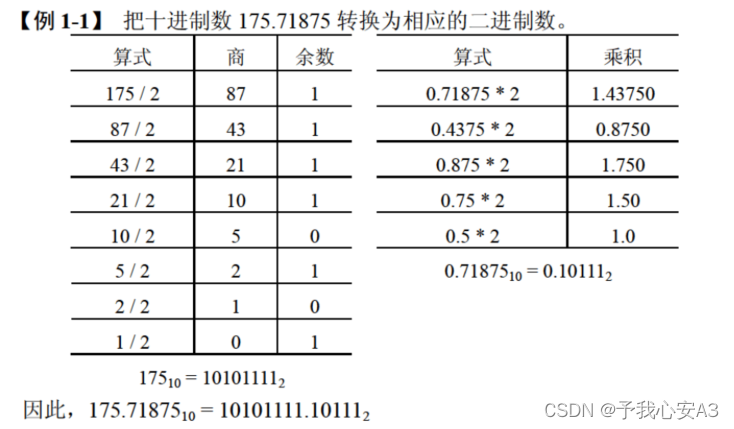
例： 0.68D = ______ B（精确到小数点后5位）
如下所示，0.68乘以2，取整，然后再将小数乘以2，取整，直到达到题目要求精度。得到结果：0.10101B
具体步骤：
0.68* 2=1.36 -->1
0.36* 2=0.72 -->0
0.72* 2=1.44 -->1
0.44* 2=0.88–>0
0.88* 2=1.76 -->1
则为：0.68D–>0.10101B
十进制转八进制
除8取余，倒序输出，小数采用“乘8取整”，顺序输出
十进制转十六进制
除16取余，倒序输出，注意10-15 用A,B,C,D,E,F替换
文章推荐
进制转化
视频推荐
最强干货，详解二进制，八进制，十进制，十六进制及其转化
1.1.2 数据的表示
数的表示-机器数
各种数据在计算机中表示的形式称为机器数，其特点是采用二进制计数制，数的符号用0、1表示，
小数点隐含表示而不占位置。机器数对应的实际数值称为数的真值。
对于带符号数，机器数的最高位是表示正、负的符号位，其余位则表示数值。
为了便于运算，带符号的机器数可采用原码、反码和补码、移码等不同的编码方法
原码
原码的表示
数值X的原码记为
[
X
]
原
[X]_原
[X]原如果机器字长为n（即采用n个二进制位表示数据），则最高位是符号位，0表示正号，1 表示负号，其余的n-1 位表示数值的绝对值。
数值0的原码有2种形式：
[
+
0
]
原
=
00000000
[+0]_原=00000000
[+0]原=00000000
[
−
0
]
原
=
10000000
[-0]_原=10000000
[−0]原=10000000
例：若机器字长n为8
[
+
1
]
原
=
00000001
[
−
1
]
原
=
10000001
[+1]_原=00000001 [-1]_原=10000001
[+1]原=00000001[−1]原=10000001
[
+
127
]
原
=
01111111
[
−
127
]
原
=
11111111
[+127]_原=01111111 [-127]_原=11111111
[+127]原=01111111[−127]原=11111111
反码
反码的表示
数值X的反码记为
[
X
]
反
[X]_反
[X]反如果机器字长为n（即采用n个二进制位表示数据），则最高位是符号位，0表示正号，1 表示负号，其余的n-1 位表示数值。正数的反码与原码相同，负数的反码则是其绝对值按位求反。
数值0的反码有2种形式：
[
+
0
]
反
=
00000000
[+0]_反=00000000
[+0]反=00000000
[
−
0
]
反
=
11111111
[-0]_反=11111111
[−0]反=11111111
例：若机器字长n为8
[
+
1
]
反
=
00000001
[
−
1
]
反
=
11111110
[+1]_反=00000001 [-1]_反=11111110
[+1]反=00000001[−1]反=11111110
[
+
127
]
反
=
01111111
[
−
127
]
反
=
10000000
[+127]_反=01111111 [-127]_反=10000000
[+127]反=01111111[−127]反=10000000
补码
补码的表示
数值X的补码记为
[
X
]
补
[X]_补
[X]补如果机器字长为n（即采用n个二进制位表示数据），则最高位是符号位，0表示正号，1 表示负号，其余的n-1 位表示数值。正数的补码与原码和反码相同，负数的补码则等于其反码的末尾加1。补码中，0有唯一编码：
[
+
0
]
补
=
[
−
0
]
补
=
00000000
[+0]_补=[-0]_补=00000000
[+0]补=[−0]补=00000000
例：若机器字长n为8
[
+
1
]
补
=
00000001
[
−
1
]
补
=
11111111
[+1]_补=00000001 [-1]_补=11111111
[+1]补=00000001[−1]补=11111111
[
+
127
]
补
=
01111111
[
−
127
]
补
=
10000001
[+127]_补=01111111 [-127]_补=10000001
[+127]补=01111111[−127]补=10000001
相对于原码和反码表示，n位补码表示法有一个例外，当符号位为1而数值位全部为0时它表示整数
2
n
−
1
2^{n-1}
2n−1，即此时符号位的1既表示负数又表示数值。
设计补码时，有意识地引用了模运算在数理上对符号位的处理，利用模的自动丢弃实现了符号位的自然处理。
用补码表示数时，由于符号位和数值部分一起编码，很难从码值形式直接判断真值的大小。
例如，45>-45，而其补码00101101在形式上小于11010011。
移码
移码的表示
移码表示法是在数X上增加一个偏移量来定义的，常用于表示浮点数中的阶码。如果机器字长为n，在偏移量为2^n-1时，只要将补码的符号位取反便可获得相应的移码表示。偏移量也可以是其他值。采用移码表示时，码值大者对应的真值就大。
例：若机器字长n为8
[
+
1
]
移
=
10000001
[
−
1
]
移
=
01111111
[+1]_移=10000001 [-1]_移=01111111
[+1]移=10000001[−1]移=01111111
[
+
127
]
移
=
11111111
[
−
127
]
移
=
00000001
[+127]_移=11111111 [-127]_移=00000001
[+127]移=11111111[−127]移=00000001
定点数与浮点数
定点数
所谓定点数，就是表示数据时小数点的位置固定不变。小数点的位置通常有两种约定方式定点整数（纯整数，小数点在最低有效数值位之后）和定点小数（纯小数，小数点在最高有效数值位之前）。
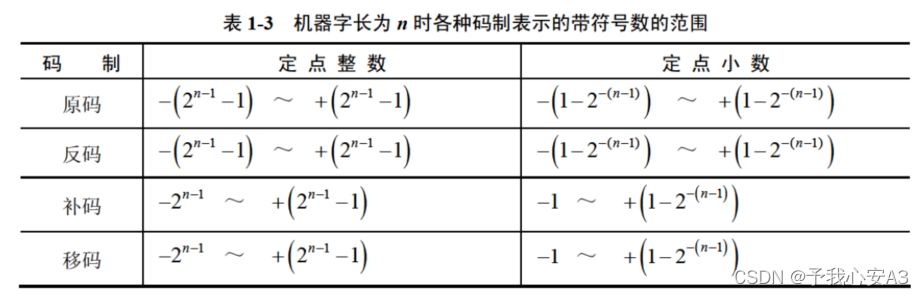
设机器字长为n，各种码制表示下的带符号数的范围如下表所示。当机器字长为n时定点数的补码和移码可表示
2
n
2^n
2n个数，而其原码和反码只能表示
2
n
−
1
2^{n-1}
2n−1个数（0表示占用了两个编码）
因此，定点数所能表示的数值范围比较小，运算中很容易因结果超出范围而溢出
浮点数
浮点数是小数点位置不固定的数，浮点表示法能表示更大范围的数。
一个含小数点的二进制数N可以表示为更一般的形式：
N
=
2
E
×
F
N=2^E \times F
N=2E×F
其中,E称为阶码，F为尾数，这种表示数的方法称为浮点表示法。
在浮点表示法中，阶码通常为带符号的纯整数，尾数为带符号的纯小数。浮点数的表示格式一般如下：
工业标准IEE 754
S为数的符号位，为0时表示正数，为1时表示负数；P为指数（阶码），用移码表示
偏移值为
2
p
−
1
−
1
，
p
为阶码的位数：
M
为尾数，用原码表示
偏移值为2^{p-1}-1，p为阶码的位数：M为尾数，用原码表示
偏移值为2p−1−1，p为阶码的位数：M为尾数，用原码表示
非数值数据的表示
ASCII码
美国标准信息交换代码
汉字编码
输入码
数字编码
拼音码
字形编码
内部码
Unicode
校验码
奇偶校验码
奇偶校验是一种简单有效的校验方法。这种方法通过在编码中增加一个校验位来使编码中1的个数为奇数（奇校验）或者偶数（偶校验），从而使码距变为 2。
奇偶校验可以检测代码中奇数个位置出错的编码，但不能发现偶数个位置出错的情况。
分为3种：水平奇偶校验法，垂直奇偶校验法，水平垂直奇偶校验法。
海明码
海明码也是利用奇偶性来检错和纠错的校验方法。海明码的构成方法是：在数据位之间插入k个校验位，通过扩大码距来实现检错和纠错。
循环冗余校验码
循环冗余校验码广泛应用于数据通信领域和磁介质存储系统中。它利用生成多项式为k个数据位产生r个校验位来进行编码，其编码长度为k+r。
1.1.3 算术运算和逻辑运算
计算机中二进制数的运算方法
’
逻辑代数的基本运算
逻辑代数是 1849 年英国数学家乔治布尔提出的，它是用代数的方式对逻辑变量进行描述和分析的数学工具，也称为布尔代数。逻辑变量的取值只有“真”和“假”，通常以1表示"真”，0表示“假”。
基本逻辑计算
与运算
全1为1，有0为0
或运算
有1为1，全0为0
非运算
1为0，0为1
异或运算
XOR
F=A⊕B=A·B’+A’·B
1.1.4 数学应用
常用数值计算（矩阵、近似求解、插值）
排列组合、应用统计
编码基础
1.1.5 常用数据结构
数组
线性表及链表
队列、栈
树
图
1.1.6 常用算法
算法与数据结构的关系
算法设计和算法描述
常用的排序算法
查找算法
常用的数值计算方法
字符串处理算法
递归算法
最小生成树、拓扑排序和单源点最短路径求解算法
1.2 计算机系统基础知识
1.2.1 硬件基础知识
1.2.1.1计算机分类和特点
1.2.1.2 中央处理器CPUCPU 的组成
常用的寄存器
指令系统，寻址方式
指令执行控制、中断控制、处理机性能
1.2.1.3 主存和辅存
存储介质
高速缓存（Cache）、主存
辅存设备
1.2.1.4 I/O 接口、I/O 设备和通信设备
I/O 接口
I/O 设备（类型、特性）
通信设备（类型、特性）
I/O 设备、通信设备的连接方法和连接介质类型
1.2.2 软件基础知识
1.2.2.1 操作系统基础知识
操作系统的类型和功能
处理机管理
存储管理
设备管理
文件管理
作业管理（作业调度算法）
图形用户界面和操作方法
1.2.2.2 程序设计语言和语言处理程序的基础知识
语言翻译基础知识（汇编、编译、解释）
程序设计语言的基本成分：数据、运算、控制和传输
程序语言类型和特点
1.2.3网络基础知识
网络的功能、分类、组成和拓扑结构
基本的网络协议与标准
常用网络设备与网络通信设备，网络操作系统基础知识
Cient/Server 结构、Browser/Server 结构
局域网（AN）基础知识
Internet 基础知识
1.2.4 数据库基础知识
数据库管理系统的主要功能和特征
数据库模式（概念模式、外模式、内模式）
数据模型、ER 图
数据操作（关系运算）
数据库语言（SQ）
数据库的主要控制功能（并发控制、安全控制）
1.2.5 多媒体基础知识
多媒体基本知识
常用多媒体设备性能特征，常用多媒体文件格式类型
1.2.6 系统性能指标
响应时间、吞吐量、周转时间
可靠性、可维护性、可扩充性、可移植性、可用性、可重用性、安全性
1.2.7 计算机应用基础知识
计算机常用办公软件操作方法
计算机信息管理、数据处理、辅助设计、自动控制、科学计算、人工智能
等领域的应用
远程通信服务
1.3 系统开发和运行知识
1.3.1 软件工程和项目管理基础知识
软件工程基础知识
软件开发生命周期各阶段的目标和任务
软件过程基本知识
软件开发项目管理基本知识
软件开发方法（原型法、面向对象方法）基础知识
软件开发工具与环境基础知识（CASE）
软件质量管理基础知识
1.3.2 系统分析设计基础知识
数据流图（DFD）、实体联系图（ER 图）基本知识
面向对象设计、以过程为中心设计、以数据为中心设计基础知识
结构化分析和设计方法
模块设计、代码设计、人机界面设计基础知识
1.3.3 程序设计基础知识
结构化程序设计、流程图、NS 图、PAD 图
程序设计风格
1.3.4 程序测试基础知识
程序测试的目的、原则、对象、过程与工具
黑盒测试、白盒测试方法
测试设计和管理
1.3.5 程序设计文档基础知识
算法的描述、程度逻辑的描述、程度规格说明书
模块测试计划、模块测试用例、模块测试报告
1.3.6 系统运行和维护基础知识
系统运行管理基础知识
系统维护基础知识
1.4 信息安全基础知识
信息系统安全基础知识
信息系统安全管理
加密与解密基础知识
1.5 标准化基础知识
标准化基本概念
标准的层次（国际标准、国家标准、行业标准、企业标准）
相关标准（代码标准、文件格式标准、安全标准、软件开发规范和文档标
准、互联网相关标准）
1.6 信息化基础知识
信息、信息资源、信息化、信息工程、信息产业、信息技术的含义
全球信息化趋势、国家信息化战略、企业信息化战略和策略常识
有关的法律、法规要点
1.7 计算机专业英语
具有助理工程师（或技术员）英语阅读水平
掌握本领域的英语基本术语
二、程序设计(下午场)
2.1 内部设计
2.1.1 理解外部设计
2.1.2 软件功能划分和确定结构
数据流图（DFD）、结构图
2.1.3 物理数据设计
确定数据组织方式、存储介质、设计记录格式，处理方式
2.1.4 详细输入输出设计
界面设计、报表设计等
2.1.5 内部设计文档
程序接口、程序功能、人机界面、输入输出、测试计划
2.1.6 内部设计评审
2.2 程序设计(下午场)
2.2.1 模块划分（原则、方法、标准）
2.2.2 编写程序设计文档
模块规格说明书（程序处理逻辑、输入输出数据格式）
测试要求说明书（测试类型和目标、测试用例、测试方法）
2.2.3 程序设计评审
2.3 程序实现
2.3.1 编程
编程方法和规范
程序设计语言的选择和使用
人工走查
程序文档化
2.3.2 程序测试
测试环境和测试工具的选择和使用
测试数据的设计
测试报告的编写
