认识时间复杂度:
O:读作big O,在数学上指的是上限的意思
常数时间的操作
一个操作如果和样本的数据量没有关系,每次都是固定时间内完成的操作,叫做常数操作。时间复杂度为一个算法流程中,常数操作数量的一个指标。常用O(读作big O)来表示。具体来说,先要对一个算法流程非常熟悉,然后去写出这个算法流程中,发生了多少常数操作,进而总结出常数操作数量的表达式。
在表达式中,只要高阶项,不要低阶项,也不要高阶项的系数,剩下的部分如果为f(N),那么时间复杂度为O(f(N))。
评价一个算法流程的好坏,先看时间复杂度的指标,然后再分析不同数据样本下的实际运行时间,也就是“常数项时间”。
俩个算法同样都是O(N)时,拼常数项,不能按照估计出来的理论值(一个是乘法操作,一个是位运算),所以需要实际去测试。
例如:
- 常数操作:int a=arr[i];
- O(N) :int b= list.get(i);//链表 遍历查找
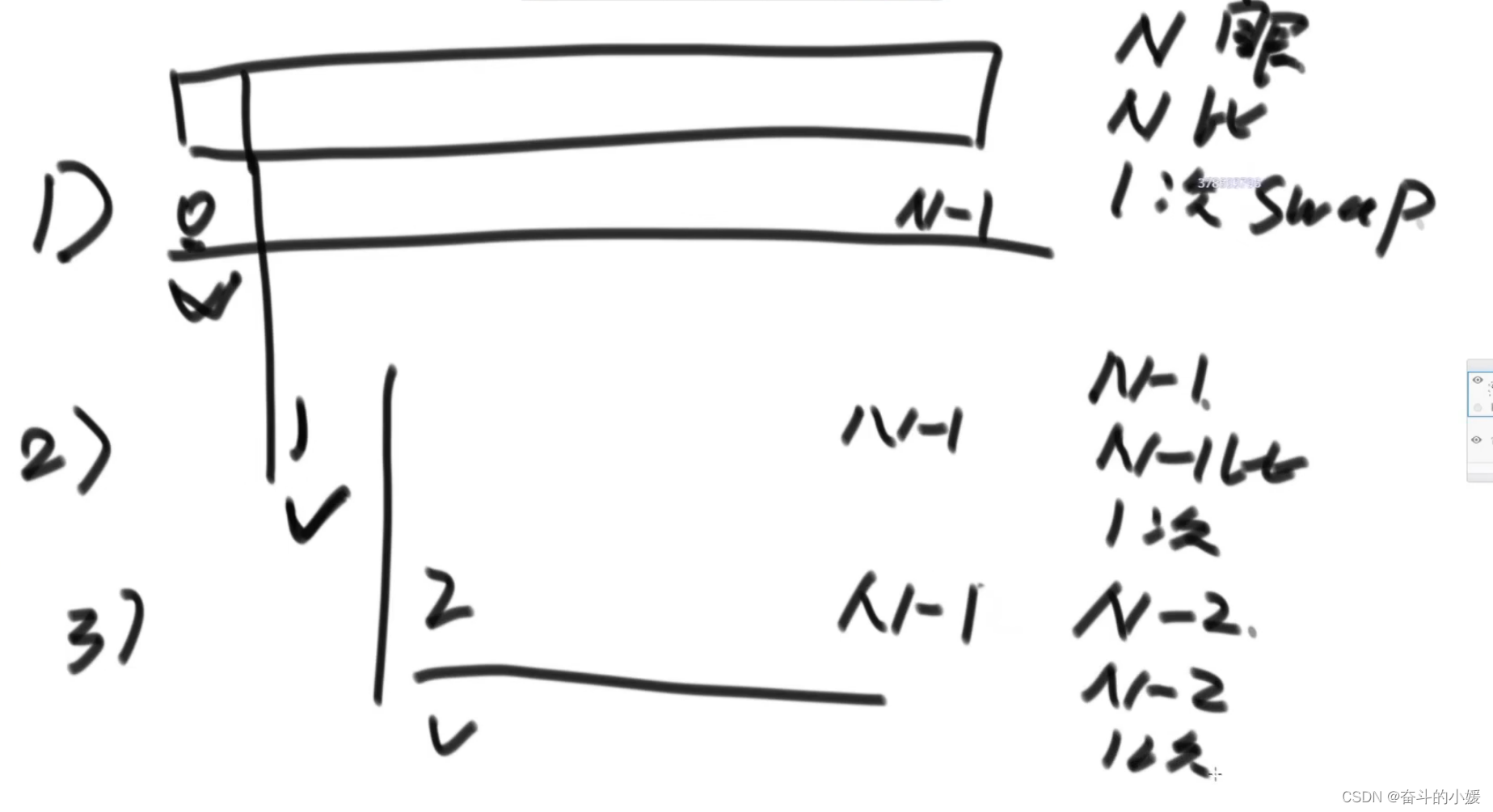
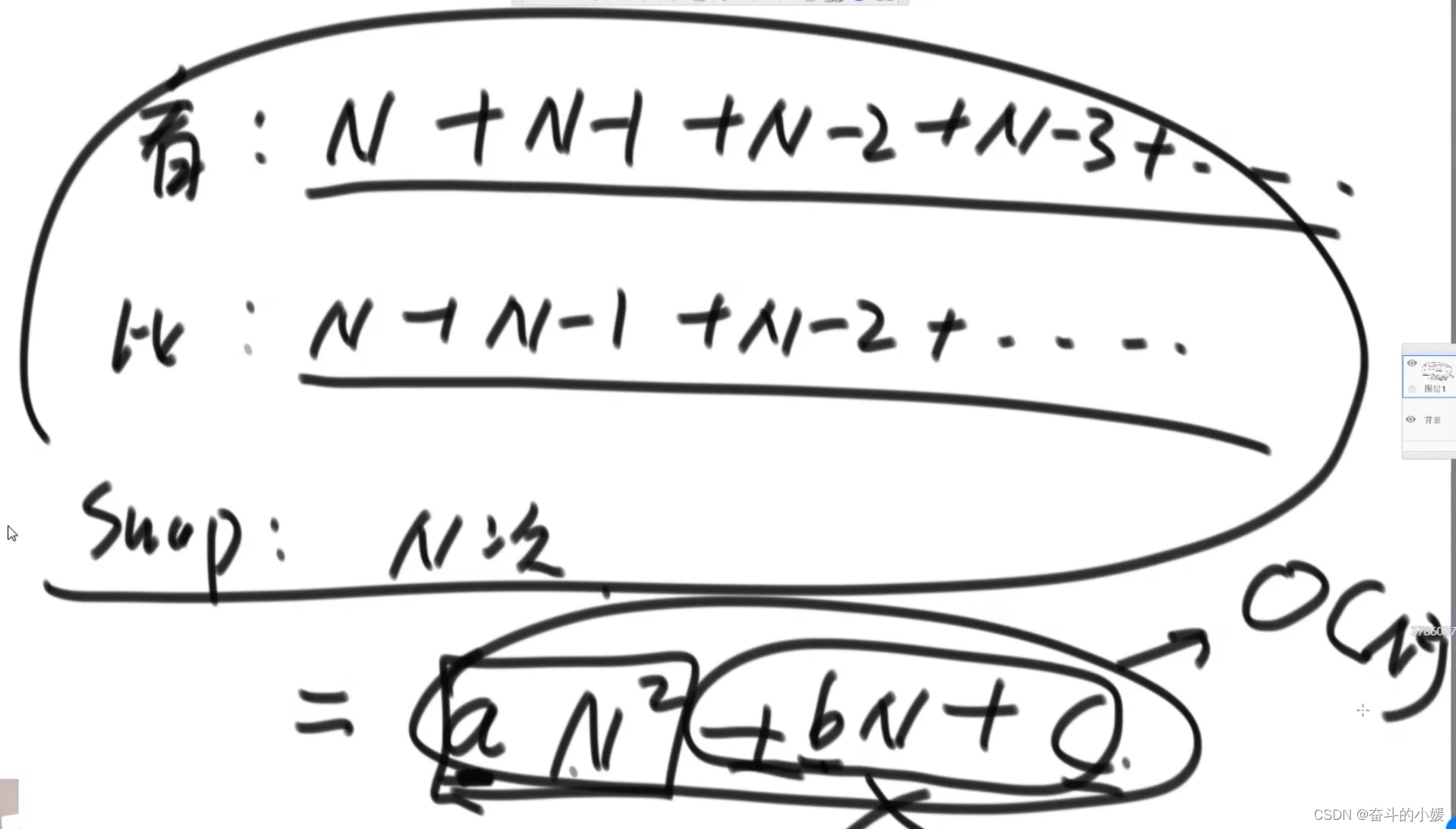
- O(n²):
选择排序:≈ aN²+bN+c≈N²(当N趋近于无穷大)