343.整数拆分

这道题全程懵逼

343. 整数拆分

class Solution {
    public int integerBreak(int n) {
        //推论一： 若拆分的数量 a 确定， 则 各拆分数字相等时 ，乘积最大。
        //推论二： 将数字 n尽可能以因子 3等分时，乘积最大。
        /**
        拆分规则：

最优： 3 。把数字 n 可能拆为多个因子 3 ，余数可能为 0,1,2 三种情况。
次优： 2。若余数为 2 ；则保留，不再拆为 1+1 。
最差： 1 。若余数为 1 ；则应把一份 3+1 替换为 2+2 ,因为 2×2 > 3×1
*/

        if(n<=3){return n-1;}
        int a=n/3;
        int b=n%3;
        if(b==0){return (int)Math.pow(3,a);}
        if(b==1){return (int)Math.pow(3,a-1)*4;}//当b==1，将一个1+3转换为2+2，因此返回3的(a-1)次方*4
        return (int)Math.pow(3,a)*2;//

    }
}

96.不同的二叉搜索树

元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量

元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量

元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量

有2个元素的搜索树数量就是dp[2]。

有1个元素的搜索树数量就是dp[1]。

有0个元素的搜索树数量就是dp[0]。

所以dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]

如图

1.确定dp数组（dp table）以及下标的含义

dp[i] ： 1到i为节点组成的二叉搜索树的个数为dp[i]。

2.确定递推公式

dp[i] += dp[j - 1] * dp[i - j]; ，j-1 为j为头结点左子树节点数量，i-j 为以j为头结点右子树节点数量

3.dp数组如何初始化

初始化，只需要初始化dp[0]就可以了，推导的基础，都是dp[0]。

4.确定遍历顺序

首先一定是遍历节点数，从递归公式：dp[i] += dp[j - 1] * dp[i - j]可以看出，节点数为i的状态是依靠 i之前节点数的状态。

5.举例推导dp数组

n为5时候的dp数组状态如图：

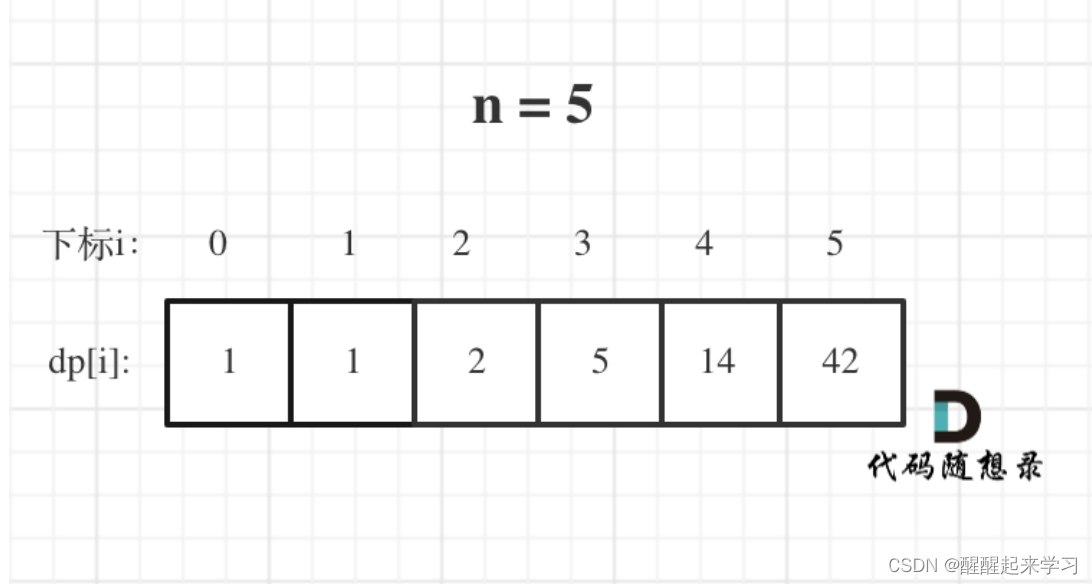
 这道题的时候想着这里的二叉树有点像是二叉搜索树

 代码实现

class Solution {
    public int numTrees(int n) {
        //这道题应该是平衡二叉树
        //1到n  dp[i] ： 1到i为节点组成的二叉搜索树的个数为dp[i]。、
        //初始化dp
        int[] dp=new int[n+1];
        //初始化0个节点和1个节点的情况
        dp[0]=1;
        dp[1]=1;
        for(int i=2;i<=n;i++){
            for(int j=1;j<=i;j++){
                //对于第i个节点，需要考虑1作为根节点直到i作为根节点的情况，所以需要累加
                //一共i个节点，对于根节点j时，左子树的节点个数为j-1，右子树的节点是i-j，相加起来就是i(把根节点算进去)
                dp[i]+=dp[j-1]*dp[i-j];
            }
        }
        return dp[n];

    }
}