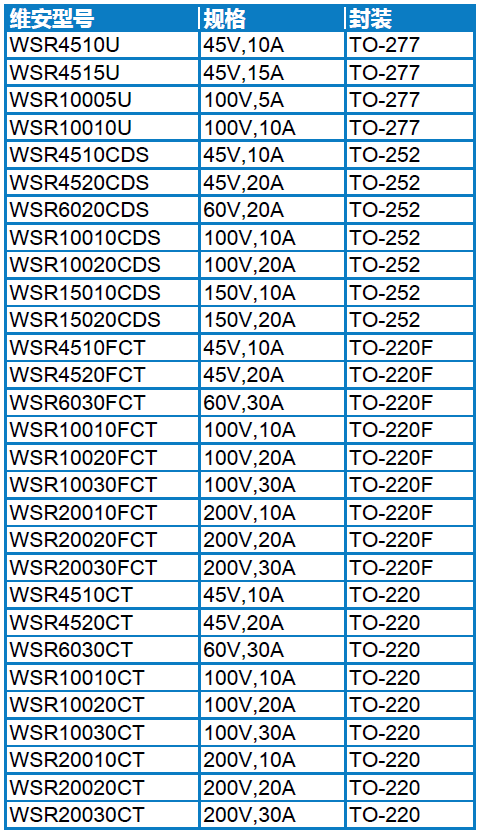
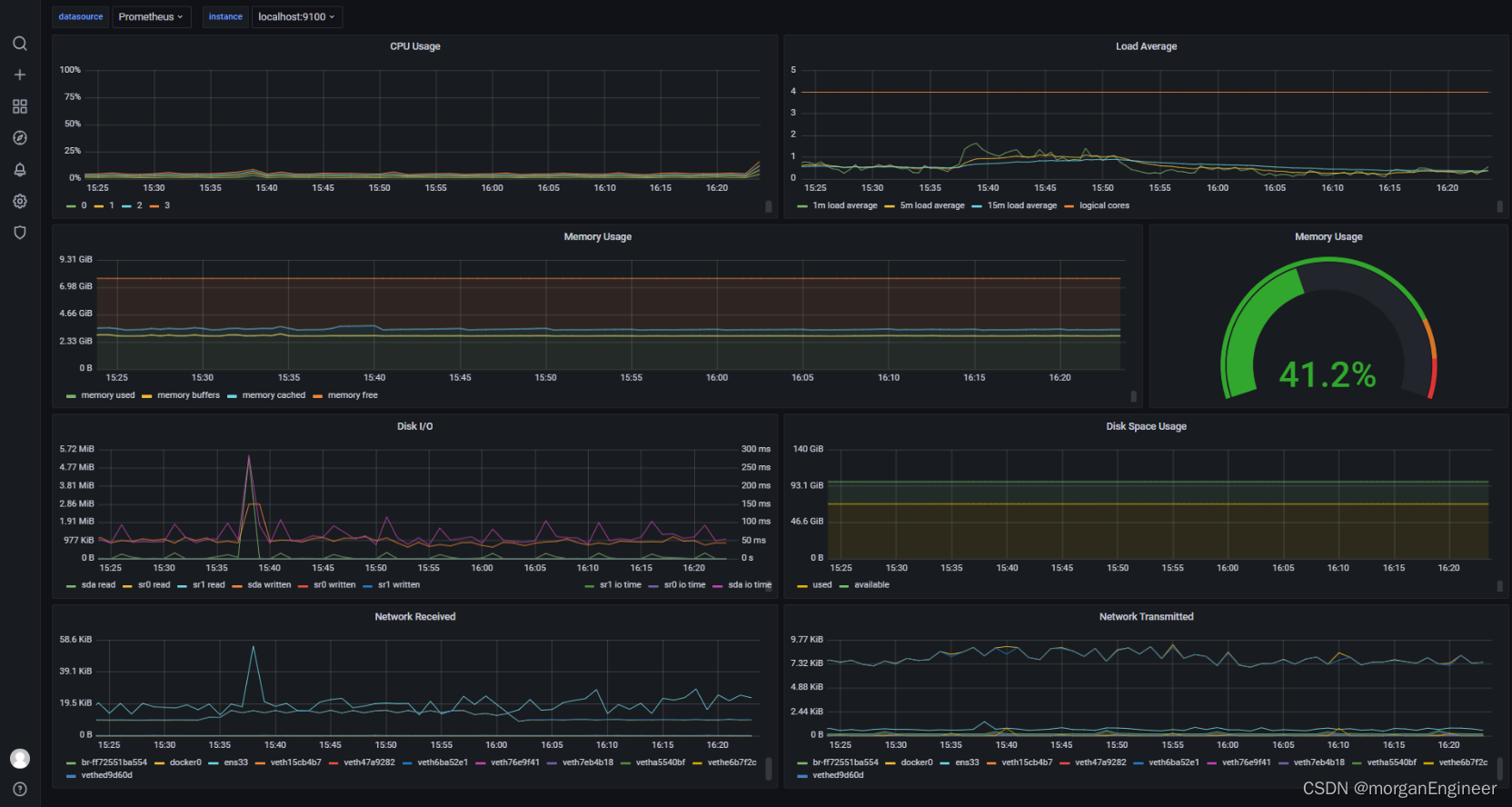
A-3 Articulation Points  分数 25

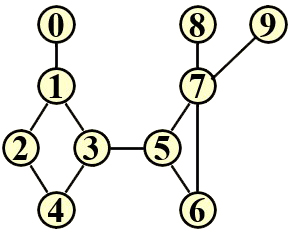
In graph theory, given a connected graph G, the vertices whose removal would disconnect G are known as articulation points. For example, vertices 1, 3, 5, and 7 are the articulation points in the graph shown by the above figure (also given by the sample input).

It is a bit complicated to find the articulation points. Here you are only asked to check if a given vertex is an articulation point or not.

Input Specification:

Each input file contains one test case. For each case, the first line contains 3 positive integers: N (≤10^3), M (≤10^4), and K (≤100), which are the number of vertices, the number of edges, and the number of queries, respectively. Then M lines follow, each gives an undirected edge in the format:

v1 v2

where v1 and v2 are the two ends of an edge. Here we assume that all the vertices are numbered from 0 to N−1. It is guaranteed that v1 is never the same as v2, and the graph is connected.

Finally a line of queries are given, which contains K vertices to be checked. The numbers in a line are separated by spaces.

Output Specification:

Output a string of 0's and 1's in a line. That is, for each query, print 1 if the given vertex is an articulation point, or 0 if not. There must be no space between the answers.

Sample Input:

10 11 8
0 1
8 7
9 7
1 2
1 3
3 5
5 7
2 4
3 4
5 6
6 7
5 2 9 1 6 3 2 7

Sample Output:

10010101

代码长度限制

16 KB

Java (javac)

时间限制

900 ms

内存限制

256 MB

其他编译器

时间限制

400 ms

内存限制

64 MB

#include<iostream>
#include<string>
#include<map>
#include<algorithm>
#include<vector>
using namespace std;
vector<vector<int>> v, vv, que;
bool status[1006];
int y, z;

void recursion(int st) {
    if (vv[st].size()==0||st==y) return;
    status[st] = true;
    for (int i = 0; i < vv[st].size(); i++)
        if(status[vv[st][i]] ==false&& vv[st][i]!=y) recursion(vv[st][i]);
}
int main() {
    int n, m, k, i, j;
    cin >> n >> m >> k;
    v.resize(n + 1);
    vv.resize(n + 1);
    for (i = 0; i < m; i++) {
        scanf("%d %d", &y, &z);
        vv[y].push_back(z);
        vv[z].push_back(y);
    }
    for (i = 0; i < k; i++) {
        cin >> y;
        fill(status, status + 1006, false);
        status[y] = true;
        if(y!=0) recursion(0);
        else recursion((y+1)%m);
        int res = -9;
        for (j = 0; j < n; j++) {
            if (j!= y && status[j] == false) {
                res = 9;
                break;
            }
        }
        if (res > 0) cout << "1";
        else cout << "0";
    }
    return 0;
}