需要源码和数据集请点赞关注收藏后评论区留言私信~~~
Mean Shift算法是根据样本点分布密度进行迭代的聚类算法,它可以发现在空间中聚集的样本簇。簇中心是样本点密度最大的地方。
Mean Shift算法寻找一个簇的过程是先随机选择一个点作为初始簇中心,然后从该点开始,始终向密度大的方向持续迭代前进,直到到达密度最大的位置。然后在剩下的点里重复以上过程,找到所有簇中心。
如何找到密度大的方向并前进多少呢?设第i个簇在第t轮迭代时簇中心位于x_i^t,则第t+1轮迭代簇中心位置x_i^t+1为:
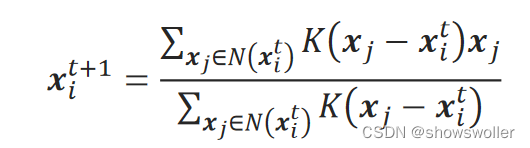
其中,N(x_i^t)是以x_i^t为中心、指定长度bandwidtℎ为半径的邻域,x_j是该邻域内的样本点。K是所谓的核函数。
假定核函数K的值取常数1,则上式为:
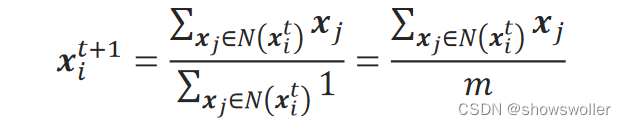
分母m是邻域N(x_i^t)中样本点的个数,分子表示邻域内各点的和。
用仅包含两个点x_1和x_2的邻域来说明上式的含义:
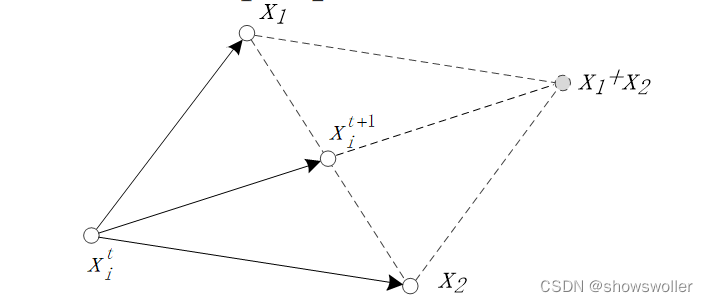
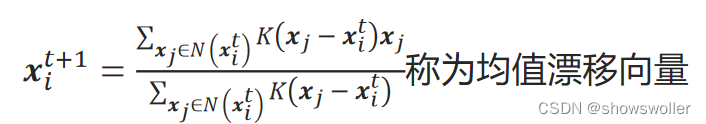
K(x_j−x_i^t)x_j可看作是对向量x_j进行了一次系数为核函数K(x_j−x_i^t)的加权。核函数K是x_j−x_i^t的函数,比如常用的高斯核函数,它的值的变化趋势与x_j到x_i^t的距离的变化趋势相反。因此,均值漂移向量可以看作是对邻域内所有样本点求加权后的均值。通过加权,使得不同距离的样本点对x_i^t+1有不同的影响。
被簇中心扫过的点计入该簇中心的簇,如果一个点被多个簇中心扫过,则计入被扫过次数最多的簇中心的簇。
简单示例如下
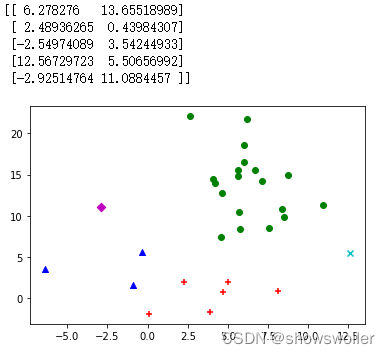
部分代码如下
ms = cluster.MeanShift(bandwidth=bandwidth, bin_seeding=True).fit(samples)
print(ms.cluster_centers_)
markers = [ 'o', '+', '^', 'x', 'D', '*', 'p' ]
colors = [ 'g', 'r', 'b', 'c', 'm', 'y', 'k' ]
linestyle = [ '-', '--', '-.', ':' ]
if len(np.unique(ms.labels_)) <= len(markers):
for i in range(len(samples)):
plt.scatter(samples[i, 0], samples[i, 1], marker=markers[ms.labels_[i]], c=colors[ms.labels_[i]])
plt.show()Mean Shift、Kmeans算法进行图像分割
mean shift算法进行图像分割
在计算机中,一幅完整的图像是由像素点组成,像素点包括由高(height)、宽(width)组成的位置信息和由红、绿、蓝组成的所谓的RGB三通道(channel)色彩信息,意思是每个像素点的颜色分别用代表红、绿、兰3种原色的亮度数据来合成表示。
用聚类的方法来分割图像,实际上是对图片中出现的颜色进行分簇。它将每一个像素点的由三原色值组成的颜色数组看成是三维空间中的一个点,然后对三维空间中的所有点进行分簇。同一簇内的点被认为颜色相似,因此,图像分割就是把不同簇的像素点分割出来。
原图如下

接下来同簇点的颜色用该簇簇中心点的颜色代替 可以明显的看到颜色有变化和暗淡了一些

单独显示簇k,其他簇都用白色代替
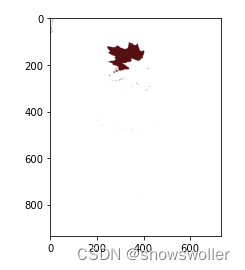
kmeans算法进行图像分割
效果如下 与上面的mean shift算法区别十分大 具体体现为颜色更加暗淡

最后 部分代码如下
#!/usr/bin/env python
# coding: utf-8
# In[1]:
import pylab
import numpy as np
from sklearn import cluster
import matplotlib.pyplot as plt
samples = np.loadtxt(r"C:\Users\Administrator\Desktop\ch3\kmeansSamples.txt")
# In[2]:
### 估计bandwidth
bandwidth = cluster.estimate_bandwidth(samples, quantile=0.2)
print(bandwidth)
# In[3]:
ms = cluster.MeanShift(bandwidth=bandwidth, bin_seeding=True).fit(samples)
print(ms.cluster_centers_)
markers = [ 'o', '+', '^', 'x', 'D', '*', 'p' ]
colors = [ 'g', 'r', 'b', 'c', 'm', 'y', 'k' ]
linestyle = [ '-', '--', '-.', ':' ]
if len(np.unique(ms.labels_)) <= len(markers):
for i in range(len(samples)):
plt.scatter(samples[i, 0], samples[i, 1], marker=markers[ms.labels_[i]], c=colors[ms.labels_[i]])
plt.show()
# ### 用Mean Shift算法进行图像分割
# In[4]:
import matplotlib.image as mpimg
from time import time
path = r"C:\Users\Administrator\Desktop\qq.jpg"
img = mpimg.imread(path)
print(type(img), img.shape, img[0,0]) # 图片加载后的数据类型、形状和(0,0)像素点的三原色值
# In[5]:
plt.imshow(img)
pylab.show()
# In[6]:
# 将二维的图像数组改为一维的,以适合聚类算法的要求
height = img.shape[0]
width = img.shape[1]
img1 = img.reshape((height*width, 3))
# In[7]:
t0 = time() # 开始计时
bandwidth = cluster.estimate_bandwidth(img1, quantile=0.4)
print(time() - t0)
# In[8]:
t0 = time() # 开始计时
ms = cluster.MeanShift(bandwidth=25, bin_seeding=True).fit(img1)
print("time", time() - t0)
# 构建一幅新的相同大小的空图片
pic_new = np.zeros((height, width, 3), dtype='i')
# 将分簇后一维标签改为二维的,与图片的形状一致
label = ms.labels_.reshape((height, width))
print(ms.cluster_centers_) # 看一下簇中心的RGB三通道值
# In[9]:
# 将簇中心三通道值改为整形的,便于显示
center = ms.cluster_centers_
center = center.astype(np.int)
# 同簇点nge(height):
for j in range(width):
pic_new[i,j] = center[label[i,j]]
plt.imshow(pic_new)
pylab.show()
# In[10]:
n_labels = len(np.unique(ms.labels_))
for i in range(n_labels): # 看一下每个簇的样本数量
print(len(np.where(ms.labels_ == i)[0]))
# In[11]:
# 单独显示簇k,其他簇都用白色代替
k = 3
center1 = center.copy()
for i in range(k):
center1[i] = np.array([255, 255, 255])
for i in range(k+1, n_labels):
center1[i] = np.array([255, 255, 255])
r j in range(width):
pic_new[i,j] = center1[label[i,j]]
plt.imshow(pic_new)
pylab.show()
# ### 用kmeans算法进行图像分割
# In[12]:
# 将图像的颜色聚类成k种,即分割成k个区域
from sklearn.cluster import KMeans
k = 3
kmeans = KMeans(n_clusters=k).fit(img1)
# 构建一幅新的相同大小的空图片
pic_new = np.zeros((height, width, 3), dtype='i')
# 将分ns.labels_.reshape((height, width))
print(kmeans.cluster_centers_) # 看一下簇中心的RGB三通道值
# In[13]:
# 将
# 同簇点的颜色用该簇簇中心点的颜色代替
for i in range(height):
for j in range(width):
pic_new[i,j] = center[label[i,j]]
plt.imshow(pic_new)
pylab.show()
# In[ ]:
创作不易 觉得有帮助请点赞关注收藏~~~