文章目录
- 前言
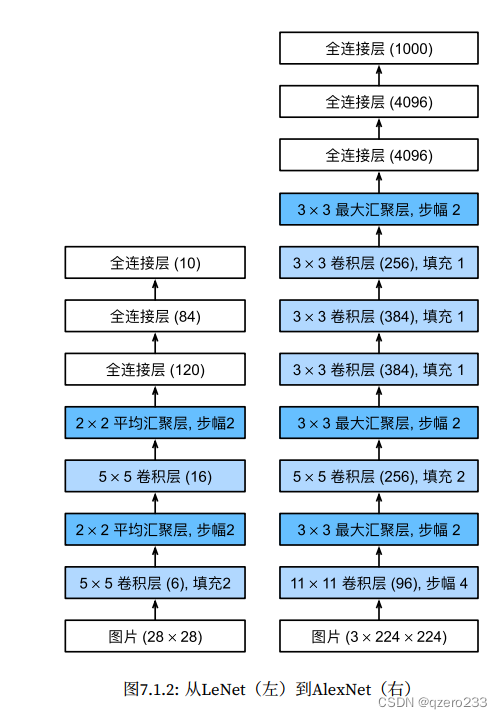
- 7.1调整参数的过程 Turing progress
- 7.2、scale
- 7.3 如果在实践中探寻超参数
- 7.4 batch normalization 批量归一化
- 7.5 将BN算法拟合到神经网络中
- 7.6 为什么 BN有效?
- 7.7测试时的BN
- 7.8 7.9 softmax regression
- 7.10深度学习的框架
前言
7.1调整参数的过程 Turing progress
对于维度小,数据少的数据,我们可以采取普通的网格搜索,对于其中的每个参数组合都进行一遍拟合模型。
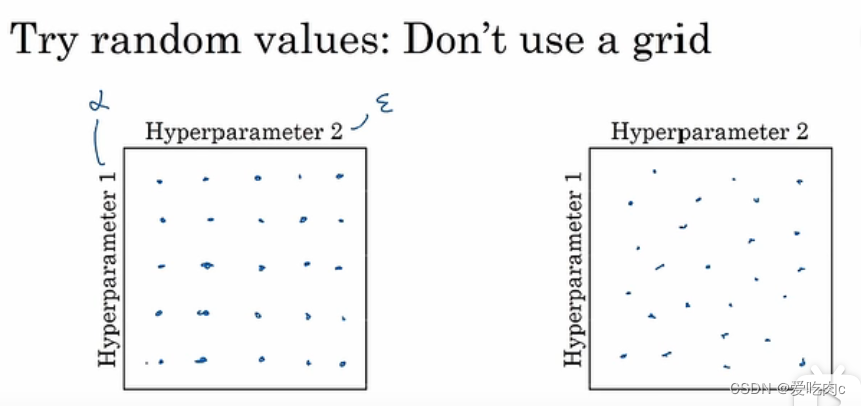
比如有两个参数,左侧的就是网格搜索。
但是这种方法并不好,如果一个超参数是学习率,一个超参数是Adam中的eplision,我们知道学习率比eplision重要太多,如果是左侧这种方法,则我们训练25个模型,但其中只相当于训练了5个,因为只取了5个不同的α值。
但是对于右侧这种随机的组合,我们同样的训练25个模型,但是其中α的取值比左侧多了不少,更有可能较快的找到一个参数组合。
这两种一个是充分搜索,一个是随机搜索,同时我们也可以随机搜索之后再采用从粗到精的搜索。

course to fine
比如我们发现圈住的点的性能都差不多,如果我们确定我们可以在这个范围内找到好的参数的话,则我们可以继续在这个方框内进行更精密的参数搜索。逐步求精。
7.2、scale
7.1我们可以选取参数空间,但是我们应该知道,这个随机均匀抽样可能并不是均匀的,我们需要选取适当的参数规模scale才可以。
比如对于学习率alpha 如果我们限定下限是0.001,上限是1的话,
我们如果采用随机搜索,那我们则百分之90的精力都放在搜索0.1-1之间的值了
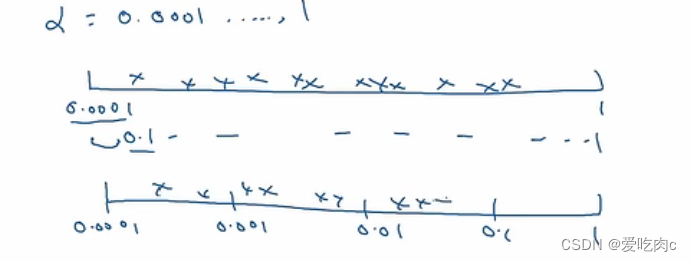
这显然是不公平的,我们应该采用适当的规模,如在对数尺度上来实现真正的随机均匀取样。
比如0.0001是10的-4次方,1是10的0次方。
在python中,我们可以这样写
r=np.random.rand()*-4 此时r的范围是【-4,0】
我们可以在-4,0中随机取值,
之后让a=10的r次方 即可得到α的值。这就是在对数尺度上来实现随机均匀取样。
比如在动量中的β
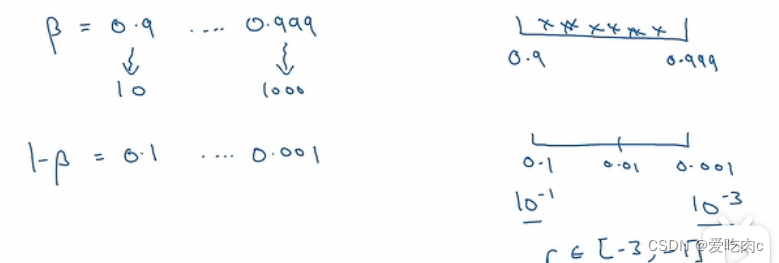
我们取下限是0.9,上限是0.999
我们可以按照1-β来 这样就变成了 0.001-0.1 就与上文α的方法相同了
7.3 如果在实践中探寻超参数
一般而言 有两种方式,
这两种方式也取决于我们CPU和GPU的性能
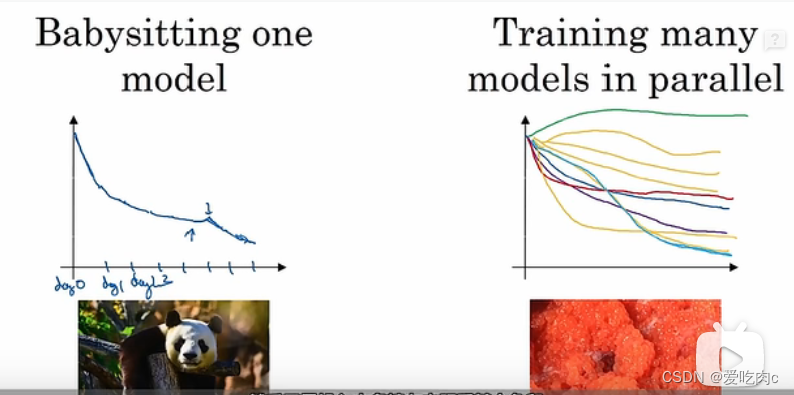
如果CPU的性能不够好,我们可能一次只能训练一个模型,之后在适当的调整参数,继续训练该模型。
如果CPU性能足以支撑我们去同时训练多个模型的话,那我们便可以采用像右图这样,并行训练多个模型,多组超参数值,这样我们只需要在一次训练之后选用性能最好的便可。
7.4 batch normalization 批量归一化
在逻辑回归中,我们讲过,采用归一化 即均值方差归一化,可以使我们的数据相对在每个维度上都更平均,能够更快的收敛,提高效率。
那么在神经网络中呢?我们当然也可以对隐藏层的z或a进行归一化。一般而言都是对z进行归一化。
比如对第二层的z进行归一化,它影响着第三层的w和b,归一化之后可以更加方便计算。
比如对第l层的z进行归一化。
采用四步。
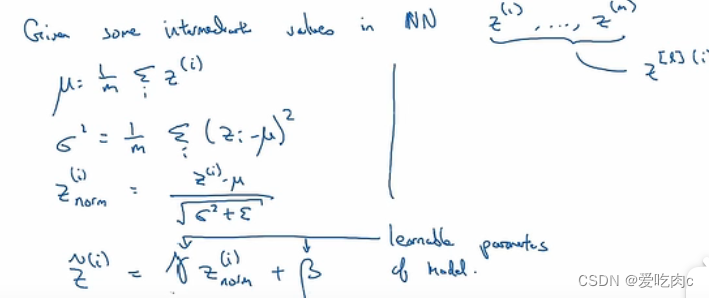
最后一步γ和β都是一个超参数。因为我们可能并不希望每一层的均值都为0,方差都为1,通过调节这两个参数,我们就可以控制任意的均值和方差了。
7.5 将BN算法拟合到神经网络中

如果是mini-batch
①: 将训练集分为m份
之后对每一份进行迭代。
②:在每一份上进行向前传播,在之前向前传播的基础上用BN算法来代替原来的Z
③计算损失函数
④向后传播,计算梯度,我们要计算dW,db,dγ 和dβ。
我们知道刚开始对z首先进行均值为0,方差为1化,所以z=W*A【L-1】+b的b是没有用的,因为b是一个常数,会被当做均值减掉,最后用beta来代替b表示偏置值,但是在实际计算梯度中我们还是会计算db。
⑤参数更新,这里我们可以采用批量梯度,也可以采用动量梯度,或者rmsprp或Adam
7.6 为什么 BN有效?
首先我们可以通过逻辑回归看出,对输入值进行归一化可以加速我们的算法效率。
其次,如果对于同一个真函数,如果x-y的映射没有变,只是x的分布变化了,协变量问题,那我们也需要重新训练模型,比如判断一幅图片是否是一只猫,这个真函数没有变,只是猫的大小颜色等分布变化的话,其实本不用重新去训练模型的。
在这个问题上,我们也可以说明BN有效,因为如果加入了BN,我们可以使神经网络后边的层数对前边层的依赖减小,因为经过BN,前边的数值的均值为0方差为1,或者均值方差是我们通过γ和β设置的其他值。尽管分布有变化,但是均值方差是没有变的,对数据变化的依赖减小。
最后这不是重要的,只是BN算法的一个额外作用而已。在mini-batch中因为是对一份一份的数据求均值与方差必然不如在整体数据上求,相当于有噪声,既然有噪声,那我们后边层数对前边的依赖减小,这与dropout有异曲同工之妙,使权重相对减小,相当于加入了一些正则化。mini-batch的size增大,相当于噪声减少,正则化程度也会相应减小。
但是我们应该知道BN主要是归一化,正则化只是一个副作用,可以忽略。
7.7测试时的BN
在训练数据集上,我们很容易便可以得到μ和方差,但是在测试数据集上,我们有时候只有一个测试数据,是没有办法求均值和方差的,所以此时我们需要估计均值和方差,以便对这个数据进行BN操作,我们可以采用指数加权的方式,把之前在mini-batch上的μ和方差都保存住,然后采用指数加权的方式来估计。
7.8 7.9 softmax regression
之前我们的分类问题都是二分类问题,采用softmax激活函数 我们可以实现多分类问题。
之前我们都是输出一个值,但是对于多分类问题我们往往需要输出这些类别的概率,就不只是一个值了。
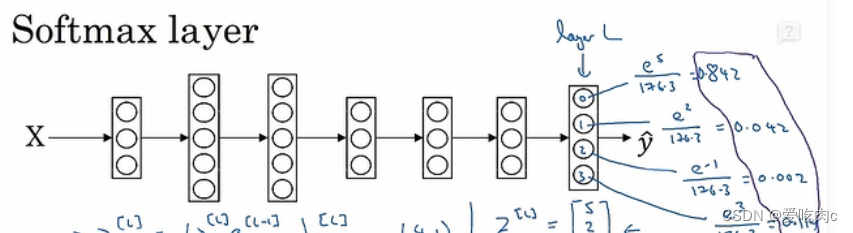
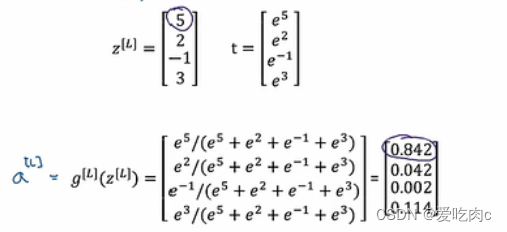
输出是每个类别的概率,之后再输出相应的类别。
那么softmax对应的损失函数又是什么呢
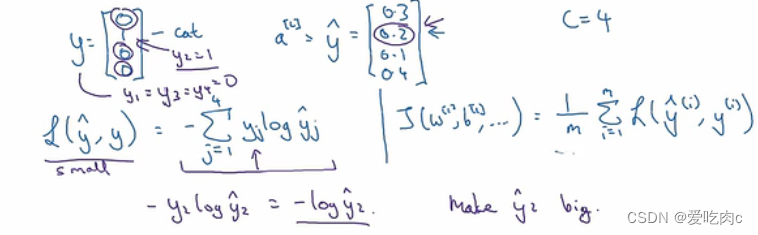
y是我们数据样本最后输出的类别,yhat是我们模型预测出来的概率
如本例中,损失函数的大小取决于yhat2,yhat2越大,则我们损失函数越小,因为最后预测出来的是第二个类别,第二个类别的概率越大则越准确。
反向传播时的一个公式
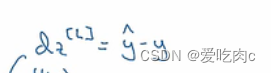
这里的y和yhat都是一个c行m列的向量,c是类别数。与之前的不同 之前是1行m列,因为之前是二分类问题,只用求得一个概率另一个概率自然也就明了。c=2时其实就相当于逻辑回归了。
7.10深度学习的框架