一、二叉树相关oj

①二叉搜索树与双向链表

二叉搜索树与双向链表链接
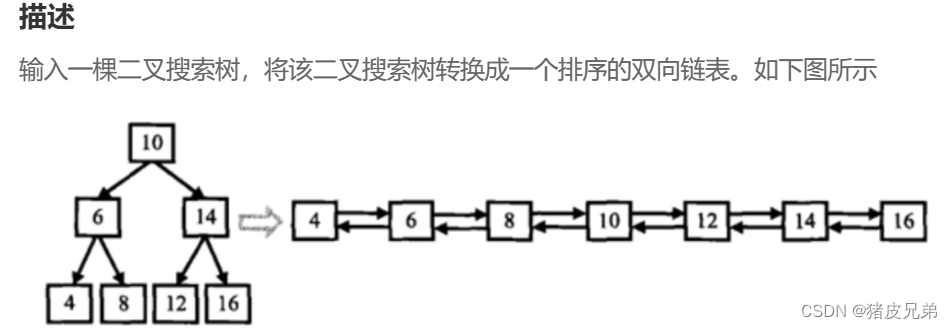
在这里插入图片描述
根据上一章搜索二叉树我们可以发现，这是搜索二叉树的中序遍历特性，所以也就是要我们对这棵树进行中序遍历，并链接起来
思路：我们可以想象它已经是遍历好的结果，我们只是对它的左右指针进行一点调节，利用递归来进行整棵树进行递归（可以认为是已经构建好了的双向链表，但是指向出了点问题，我们要通过对树的中序遍历这种方式来顺序访问到双向链表中的各个结点来修改指向）

class Solution {
public:
	TreeNode*prev=nullptr;
	TreeNode*head=nullptr;
    TreeNode* Convert(TreeNode* pRootOfTree) {
		if(pRootOfTree==nullptr) return nullptr;
		Convert(pRootOfTree->left);//找到头
		pRootOfTree->left = prev;
		if(prev) prev->right = pRootOfTree;
		prev = pRootOfTree;//前指针后移
		head = head==nullptr?pRootOfTree:head;//空的话就找这个头，不然就不变
		Convert(pRootOfTree->right);//继续遍历，代表想象链表后移
		return head;
    }
};

②前序遍历和中序遍历构造二叉树

前序遍历和中序遍历构造二叉树链接
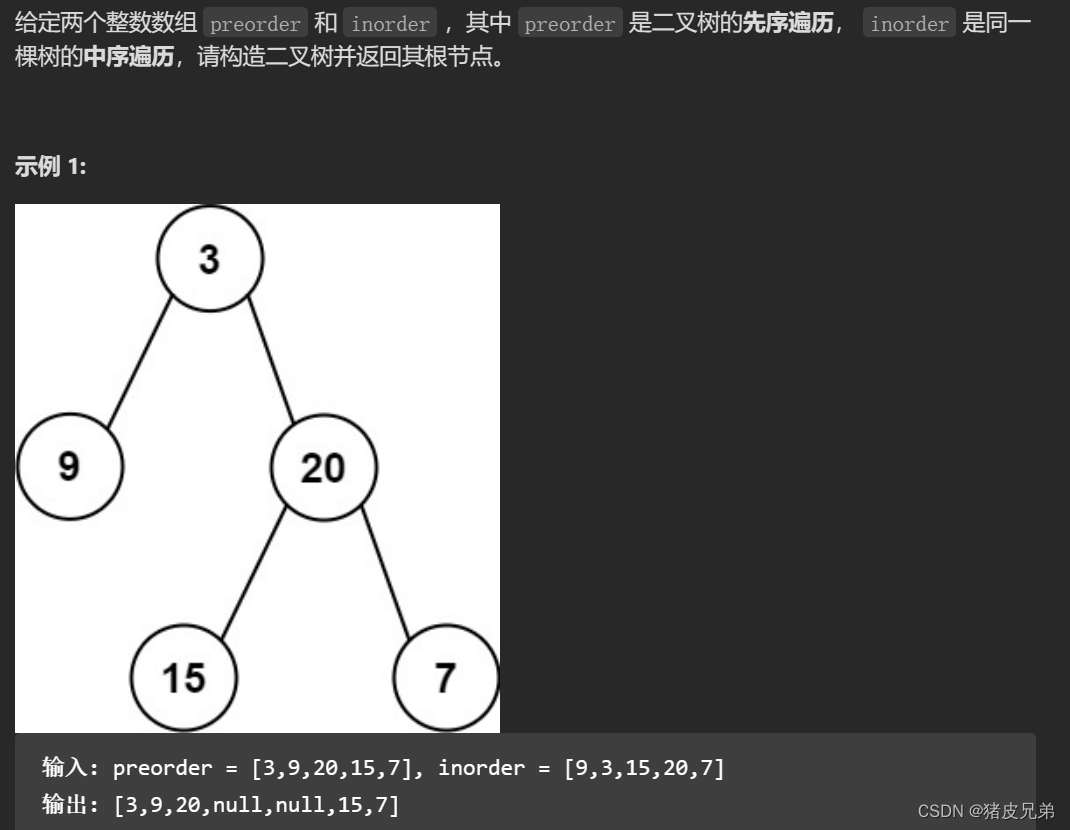
在这里插入图片描述
从前序遍历和中序遍历的特性中我们可以看出，前序遍历先访问根结点，再访问左子树，再访问右子树，中序遍历先访问左子树，再访问根结点，再访问右子树，所以我们可以通过前序遍历来找到中序遍历的左子树和右子树

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int move=0;
    TreeNode*buildTreeHelper(vector<int>&preorder,vector<int>&inorder,int start,int finish)
    {
        if(start>=finish)
        return nullptr;
        int target=0;
        for(int i=start;i<finish;i++)
        {
            if(preorder[move]==inorder[i])
            {
                target=i;
                move++;//找每一个根
                break;
            }
        }
        TreeNode* ret =  new TreeNode(inorder[target]);
        ret ->left = buildTreeHelper(preorder,inorder,start,target);//构造左树,左闭右开区间
        ret ->right = buildTreeHelper(preorder,inorder,target+1,finish);//构造右树
        return ret;        
    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        if(preorder.size()==0) return nullptr;
        return buildTreeHelper(preorder,inorder,0,preorder.size());//构造
    }
};

二、二叉树的非递归

①前序遍历非递归

借助一个栈，一直遍历左树，并放进栈和返回的数组，当没有左时，就取出栈的top(),拿到该结点的右子树的根结点，然后重复上述操作，前序遍历的特点就是优先遍历根，再左树，再右树
二叉树的前序遍历非递归

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> ret;
        if(root==nullptr) return ret;
        st.push(root);
        TreeNode*cur= st.top();
        while(!st.empty())  
        {
            while(cur)
            {
                ret.push_back(cur->val);
                st.push(cur);
                cur=cur->left;  
            }
            TreeNode*tmp= st.top();
            st.pop();
            if(tmp&&tmp->right) 
            {
                cur = tmp->right;
            }
        }
        return ret;
    }
};

②中序遍历非递归

中序遍历的特点就是先访问左子树再访问根再访问右子树，把前序遍历稍微变一变即可，比如先入栈，等左子树入栈完了，开始从栈中取top，此时再去入返回数组，所以直接去遍历右子树一样的操作即可

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> ret;
        if(root==nullptr) return ret;
        st.push(root);
        TreeNode*cur= root->left;
        while(cur||!st.empty())  
        {
            while(cur)
            {
                st.push(cur);
                cur=cur->left;  
            }
            TreeNode*tmp= st.top();
            ret.push_back(tmp->val);
            st.pop();
            if(tmp&&tmp->right) 
            {
                cur = tmp->right;
            }
        }
        return ret;
    }
};

③后序遍历非递归

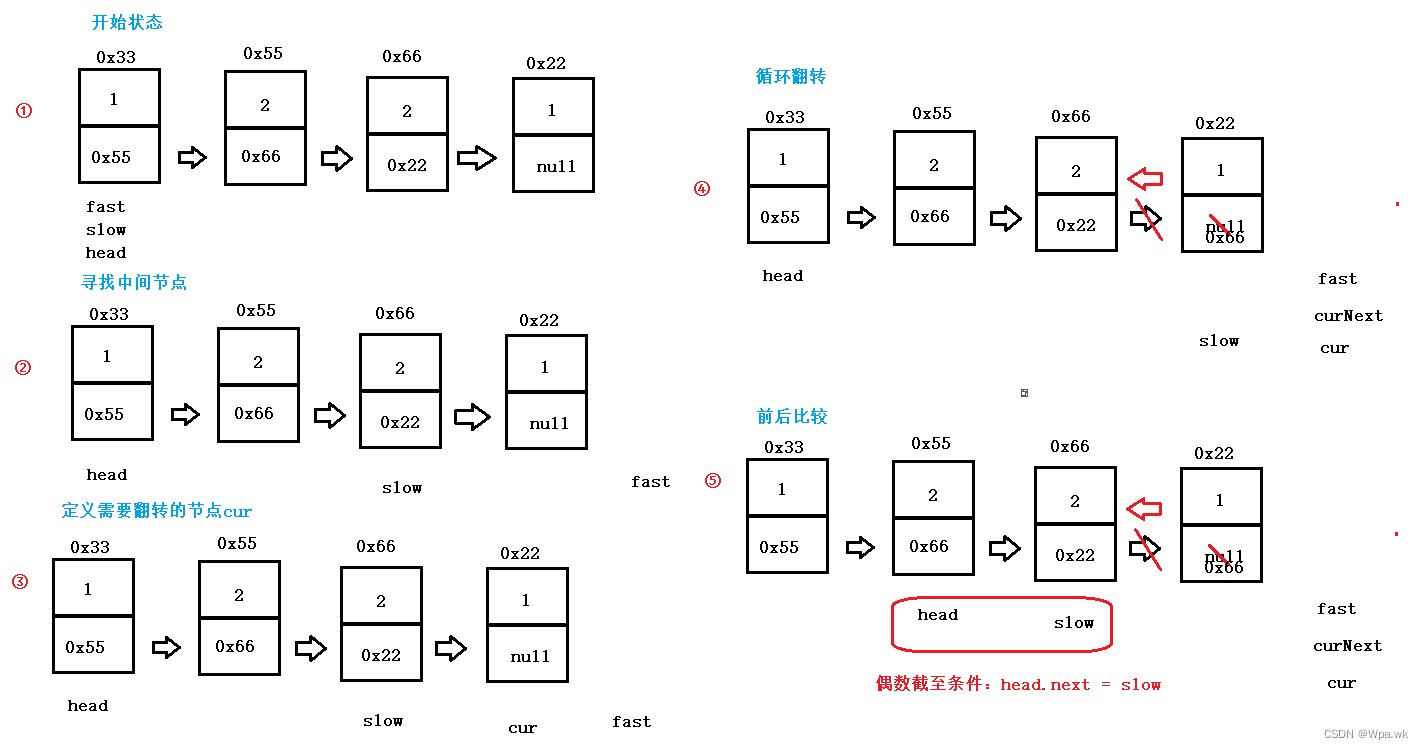
后序遍历的特点是先访问右子树，再访问左子树，再访问根，通过一个prev来存储上一次遍历的结点，来判断是否需要往右遍历，避免死循环

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        //根右左，再逆序
         stack<TreeNode*> st;
        vector<int> ret;
        if(root==nullptr) return ret;
        st.push(root);
        TreeNode*cur= root->left;
        TreeNode*prev=nullptr;
        while(!st.empty())  
        {
            while(cur)
            {
                st.push(cur);
                cur=cur->left;  
            }
            TreeNode*tmp = st.top();
            if(tmp->right==nullptr||tmp->right==prev)
            {
                ret.push_back(tmp->val);
                prev=tmp;//prev就是遍历该结点时的上一个结点
                st.pop();
            }
            else
            {
                cur= tmp->right;//直到返回到有右结点并没有遍历过的时候cur才发挥作用，不然又会去遍历左树
            }
        }
        return ret;
    }
};