目录

6265. 统计相似字符串对的数目 - ac

6266. 使用质因数之和替换后可以取到的最小值 

分解质因数

1、tle代码

2、优化ac代码

6267. 添加边使所有节点度数都为偶数 - 建图+分类讨论

关于建图 

6268. 查询树中环的长度 - LCA最近公共祖先

---

6265. 统计相似字符串对的数目 - ac

class Solution {
public:
    int similarPairs(vector<string>& words) {
        int res=0;
        
        for(int i=0;i<words.size()-1;i++)
        {
            set<char>s1;
            
            for(int j=0;j<words[i].size();j++) s1.insert(words[i][j]);
            for(int j=i+1;j<words.size();j++) 
            {
                set<char>s2;
                for(int k=0;k<words[j].size();k++) s2.insert(words[j][k]);
                if(s1==s2) res++;
            }
        }
        return res;
    }
};

6266. 使用质因数之和替换后可以取到的最小值 

分解质因数

for(int i=2;i<=x/i;i++)
    if(x%i==0) //i一定是质数
    {
        int cnt=0;
        while(x%i==0) x/=i,cnt++;
        cout<<i<<' '<<cnt<<endl; //输出质因数 次方数
    }
if(x>1) cout<<x<<' '<<1<<endl;

1、tle代码

思路大体是对的 但是搞错了题目一个点 

当某数的质因数为1 和本身时  质因数之和=本身

我当时想成 质因数之和=1+本身了 1不是质数！！！

class Solution {
public:
    bool isprime(int x)
    {
        if(x<2) return false;
        for(int i=2;i<=x/i;i++)
            if(x%i==0) return false;
        return true;
    } 
    
    int smallestValue(int n) 
    {
        int minx=0x3f3f3f3f;
        int sum=n;
        if(isprime(n)) return n;
        
        while(true)
        {
            n=sum;
            if(isprime(n)) break;
            sum=0;
            for(int i=2;i<=n/i;i++)
            {
                int cnt=0;
                if(n%i==0)
                {
                    while(n%i==0) n/=i,cnt++;
                }
                while(cnt--) sum+=i;
            }
            if(n>1) sum+=n;
            minx=min(minx,sum);
        }
        
        return minx;
    }
};

2、优化ac代码

class Solution {
public:
    int yin(int n)
    {
        int sum=0;
        for(int i=2;i<=n/i;i++)
            if(n%i==0)
            {
                while(n%i==0) n/=i,sum+=i;
            }
        if(n>1) sum+=n;
        return sum;
    }
    
    int smallestValue(int n) 
    {
        int cnt=0;
        while(true)
        {
            int x=yin(n);
            if(x==n) break;
            n=x;
        }
        return cnt;
    }
};

class Solution {
public:
    int smallestValue(int n) 
    {
        int t;
        while(true)
        {
            t=n;
            int num=0;
            for(int i=2;i<=n/i;i++)
            {
                if(n%i==0)
                {
                    while(n%i==0) n/=i,num+=i;
                }
            }
            if(n>1) num+=n;
            if(t==num) break;
            n=num;
        }
        return t;
    }
};

 

6267. 添加边使所有节点度数都为偶数 - 建图+分类讨论

6267. 添加边使所有节点度数都为偶数

思路：

• 先统计奇度数点 存序号
• 分类讨论可能满足条件的情况
• 如果奇度数点==0 则不用连直接return true
• 如果奇度数点==2

        如果两点间没有连线 则只要连接这两个点就true

        如果两点间有连线 则找出一个除a b点外的点c 如果该点和a b都没有连线 则两条边可以c-a 和c-b 也true

• 如果奇度数点==4 如果两两可以相连则true（满足任意一种两两相连情况）
• 除以上情况外都为false

关于建图 

• 本题用map存图   map<PII，int> e
• e[{a,b}]=e[{b,a}]=1 无向图 a b点间有连线
• 判断a b点间是否相连   e.count({a,b})

class Solution {
public:
    static const int N=1e5+10;
    bool isPossible(int n, vector<vector<int>>& edges) {
        int d[N]={0};
        map<pair<int,int>,int> e;
        for(vector<int>& x:edges)
        {
            int a=x[0],b=x[1];
            d[a]++,d[b]++;
            e[{a,b}]=e[{b,a}]=1;
        }
        vector<int> v;
        for(int i=1;i<=n;i++) if(d[i]%2) v.push_back(i);

        if(v.size()==0) return true;
        else if(v.size()==2)
        {
            int a=v[0],b=v[1];
            if(!e.count({a,b})) return true; //如果a b两点间不存在连线 则将两点相连即可

            //否则找一个偶度数节点分别连接a和b 这样偶度数+2还是偶数 两个奇度数点+1也是偶数
            for(int i=1;i<=n;i++) 
                if(i!=a&&i!=b&&!e.count({i,a})&&!e.count({i,b})) return true;
        }
        else if(v.size()==4)
        {
            int a=v[0],b=v[1],c=v[2],d=v[3];
            //如果四个点能两两相连 满足任意一种情况即可 否则false
            if(!e.count({a,b})&&!e.count({c,d})) return true;
            if(!e.count({a,c})&&!e.count({b,d})) return true;
            if(!e.count({a,d})&&!e.count({b,c})) return true;  
        }
        return false;
    }
};

 

6268. 查询树中环的长度 - LCA最近公共祖先

6268. 查询树中环的长度

对于两个点 a 和 b，每次把深度更深的点往父节点移一步，直到它们走到同一个点，即可求ab两点到LCA距离之和

环长度 = ab两点到LCA距离之和+1

思路：

• 因为是完全二叉树 所以深度和节点序号很规律 某节点序号/2就是父节点

• 环可以看成是从 a 出发往上走，在某个位置「拐弯」，往下走到 b。

  这个拐弯的地方就是 a 和 b 的最近公共祖先LCA。

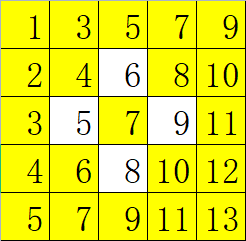
• 第一个图 5和3相连 则它们的LCA是1  环长度=5到1距离+3到1距离+1

 

• 如何找LCA？

  不断循环，每次循环比较 a 和 b 的大小：

  如果 a>b，则 a 的深度大于等于 b 的深度，那么把 a 移动到其父节点，即 a=a/2；
  如果 a<b，则 a 的深度小于等于 b 的深度，那么把 b 移动到其父节点，即 b=b/2；
  如果 a=b，则找到了LCA，退出循环。

class Solution {
public:
    vector<int> cycleLengthQueries(int n, vector<vector<int>>& q) {
        vector<int> ans;
        for(int i=0;i<q.size();i++)
        {
            int res=1;
            int a=q[i][0],b=q[i][1];
            while(a!=b)
            {
                a>b? a/=2:b/=2;
                res++;
            }
            ans.push_back(res);
        }
        return ans;
    }
};