1. 问题

2. “function”是如何翻译成“函数”的？

3. “function”是谁引入数学中的，其意义何在？

3.1 “function”的词源

3.2 “function”引入数学中

3.3 “function”的含义

4. 常见的函数(Common Functions)

4.1 线性函数(Linear Functions)

4.2 幂函数(Power Functions)

4.3 多项式函数(Polynomial Functions)

4.4 有理函数(Rational Functions)

4.5 三角函数(Trigonometric Functions)

4.5.1 角度或角(Angles)

4.5.2 六种基本的三角函数

4.6 指数函数(Exponential Functions)

4.7 对数函数(Logarithmic Functions)

5. 何谓代数函数(Algebraic Functions)

6 何谓超越函数(Transcendental Functions)

7. 组合函数及移动和缩放图像(Combining Functions; Shifting and Scaling Graphs)

7.1 函数四则运算(求和，求差，相乘，和商式)(Sums, Differences, Products, and Quotients)

7.2 复合函数(Composite Functions)

7.3 移动函数图像(Shifting a Graph of a Function)

7.4函数图像的伸缩和反射(Scaling and Reflecting a Graph of a Function)

1. 问题

“函数”这个中文名称，在英语中对应的单词为“function”。那么，在数学中它到底是什么意思呢？有没有直观的方式去理解它呢？因为很多人讨厌数学，就是从接触“函数”开始的。简中教材几乎不会告诉你“函数”这个概念是怎么来的，它代表的意义又是什么，它仅仅是一个名称呢，还是说字面也代表了其内涵？“函数”在教材中第一次出现，教材就默认学习者已经知道这个概念。如果你要问老师“函数”到底是什么，他就开始搬定义了，满足某条件，它就是“函数”，例如，某定义:

一般地，在一个变化过程中，如果有两个变量x和y，并且对于x的每一个确定的值，y都有唯一确定的值与其对应，那么我们就把x称为自变量，把y称为因变量，y是x的函数。

2. “function”是如何翻译成“函数”的？

“函数”这个名称是从英语单词“function”翻译而来的，那么是谁将它翻译成“函数”这个名称的呢？其想表达的内涵又是什么？其字面意义有没有表示一定的本质意义，还是说仅仅是随意取的一个名称，就像人的名字一样，只是个称呼呢？

目前流传的一个可查的版本，是这个译名出自清代数学家李善兰。清代数学家李善兰(1811-1882)在1859年和英国传教士伟烈亚力(Alexander Wylie)合译的《代微积拾级》中首次将“function”译作“函数”。《代微积拾级》这布译作，目前还能查到，估计在某些收藏馆还存在，其中，现在数学中用的很多概念的汉译名，都有他的影子，所以后来的数学人也就沿用他的译名，作了很小的改动。网上找了几张旧书的图，看看啥样子：

为什么李善兰将“function”翻译为“函数”呢？下面分别看一下“函”字和“含”字的意义。

【函】(hán)

(1) 包含，容纳。诗周颂载芟：“播厥百谷,实函斯活。”

(2) 铠甲。周礼考工记：“燕无函。”

(3) 封套叫函，信件一封叫一函。文选三国魏吴季重(质)答东阿王书：“发函申纸，是阿文采之巨丽，而慰喻之绸缪乎！”

(4) 匣，盒子。如剑函，镜函。

(5) 函谷关的省称。

(6) 舌[说文]。

(7) 宽阔。<文选.左思.吴都护>[伊兹都之函弘。]

(8) 怀。

(9) 姓。

【含】(hán)

(1) 口中衔(xián)物。庄子马蹄：“含哺而熙。”

(2) 包而未露。如，含怒、含情。

(3) 怀藏。<战国策.秦策一>[含怒日久。]

(4) 宽容。含宥。

(5) 食。<法言.孝至>[子有含菽缊絮而致滋美其亲]。

(6) 形容茂盛的样子。含含。

从这两个字的意义来看，在古汉语中，“函”字更体现“包含，容纳”之意，因此选用了“函”字；后来的发展，现今容纳使用“含”字。

我国古代并不用符号来表示未知数,而是用筹算来解方程。至宋、元时代李治的「天元术」,用「立天元」表示未知数,并在相应的系数旁写一个“元”字以为记号。至元朝朱世杰(约公元13 世纪)用天、地、人、物表示四个未知数,建立了四元高次方程组理论。数学中的消元问题中元的叫法也由此而来。

李善兰认为：“凡式中含天，为天之函数”（凡是公式中含有变量x(未知数)，则该式子叫做x的函数）。即凡此变数中函彼变数者，则此为彼之函数。他认为，彼数是由此数通过某种变化关系而得到，因此彼在某种关系上包含此，而反之则不然。因此，“函”的意义即体现在这里。

3. “function”是谁引入数学中的，其意义何在？

3.1 “function”的词源

function[ˈfʌŋkʃ(ə)n] n. 始于1530年代，意为“one's proper work or purpose; power of acting in a specific proper way(一个人的正当工作或目的——功能；以特定的适当方式行事的权力——职责)”，来自于法语“function”(16世纪)，其直接来源是拉丁语的“functionem”(其主格为“functio”)，意为“a performance, an execution(履行、执行)”，来自“funct-”的动作名词，“funct-”是“fungi ”的过去分词词干，意为“perform, execute, discharge(履行、执行、执行任务)”，来自印欧语“*bhung-”(*号表示推测，并无原始文字记载)，意为“be of use, be used(使用)”。从词源看出，“function”的意义不外乎“履行任务、执行某项功能、功能、职责”。

3.2 “function”引入数学中

而表示“彼变化由此变化引起”的这种数学概念发生于公元17世纪。在这段时期，Rene Descartes(笛卡尔) (1596-1650)在他的书<<Geometry>>(<<几何学>>1637年)中，使用这个概念来描述很多数学关系。“function”这个术语，据称最早是由Gottfried Wilhelm Leibniz(莱布尼兹)(1646-1716)引入数学中的，几乎是在笛卡尔的<< Geometry>>出版五年之后。

Leonhard Euler(欧拉)(1707-1783)进一步规范化了“函数”这个概念，并引入了y = f(x)这种记法(读作“y等于x的f”)。

3.3 “function”的含义

在数学中，“函数”表示定义一个变量(称为“the independent variable”,即“独立变量”，教材中一般称为“自变量”，即不依赖于另一个变量的变量)与另一个变量(称之为“the dependent variable”，即“依赖变量”，教材中译为“因变量”，即其值依赖另一个变量)之间的一种关系的一种表述、一种规则、或者法则。函数在数学中是普遍存在的，是科学中公式化物理关系的基础。

第一个现代的函数定义德国数学家Peter Dirichlet(狄利克雷)在1837年作出的：

“If a variable y is so related to a variable x that whenever a numerical value is assigned to x, there is a rule according to which a unique value of y is determined, then y is said to be a function of the independent variable x.(假如无论何时给变量x赋一个数值，都有一个与之如此紧密关联的变量y，存在一个法则，根据这个法则，可以确定与这个x关联的y值具有唯一性，则说成y是自变量x的函数。)”

这种关系通常符号化为y = f(x)——读成“y等于x的f”,以上提过，这种记法是由欧拉引入——并且，y和x的关系表现为，对于每一个x，都有一个唯一的y值与之对应。即，对于同一个x值，不能有一个以上的y值与之对应。使用集合理论的语言，可以表述为函数将一个集合中的元素x与另一个集合中的元素f(x)关联了起来。x值的集合称为函数的域(domain，教材中一般称为“定义域”)，由这个定义域中的x值产生的f(x)值的集合称为这个函数的范围(range，教材中一般称为“值域”)。此外，也有用其它的符号用于表示自变量x的函数，例如g(x)和P(x)，特别是当函数特征未知或未明确的时候。用集合将函数定义为如下形式：

“A function ƒ from a set D to a set Y is a rule that assigns a unique value ƒ(x) in Y to each x in D.(从一个集合D另一个集合Y的函数是一个法则，这个法则对于集合D中的每一个x值，都在集合Y中给它赋予了一个唯一的对应值ƒ(x))”(即核心就是“函数是一个法则”)。

通常，函数由一个描述如何从一个输入值计算出输出值的公式指定。例如，等式A = πr2 是一个由半径计算圆的面积A的法则。

4. 常见的函数(Common Functions)

在微积分中，会遇到各种类型的重要函数。

4.1 线性函数(Linear Functions)

形如 ƒ(x) = mx + b (其中，m和b是常量)的函数称为线性函数。线性关系，指量也量之间的比例成直线的关系，在空间和时间上代表规则和光滑的运动。

4.2 幂函数(Power Functions)

形如 $f(x)={x}^{a}$ (其中，a是一个常数)的函数称为幂函数。对于幂函数，有几个重要的案例。

(a) $f(x)={x}^{a}$ (其中，a是一个常数)的幂函数,当x=a时，函数是一个正整数。

(b) $f(x)={x}^{a}$ (其中，a是一个常数)的幂函数,当a= -1或a= -1时，函数成为ƒ(x)=1/x (x≠0，关于原点对称), $g(x)=1/x^{2}$ (x≠0，关于y轴对称)。

4.3 多项式函数(Polynomial Functions)

形如以下形式的函数称为多项式：

$p(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+...+a_{1}x+a_{0}$

式中，n为一个非负整数， $a_{0},a_{1},...,a_{n},$ 是实数常量(称为多项式的系数(coefficients))，所有多项式的域都是(-∞,+∞)。

如果这个前导的系数 $a_{n}$ ≠0，则n称为多项式的度(degree)(某些教称可能称为多项式的“次数”)，可以用多项式函数来解释线性函数，m≠0的线性函数就是度为1的多项式函数。度为2的多项式函数通常写作 $p(x)=ax^{2}+bx+c$ ，称为二次函数(平方函数)(quadratic functions)。类似地，类为3的多项式 $p(x)=ax^{3}+bx^{2}+cx+d$ 称为三次函数(立方函数)(cubic functions)。

4.4 有理函数(Rational Functions)

有理函数是一个商(quotient)或比率(ratio),表示为 $f(x)=\frac{p(x))}{q(x)}$ 其中p(x)和q(x)是多项式，有理函数的域为使得q(x)≠0的所有实数x的集合。

4.5 三角函数(Trigonometric Functions)

三角函数有6种基本类型。

4.5.1 角度或角(Angles)

角度或角(angles)是通过度(degrees)或者弧度(radians)来度量。先看一张图

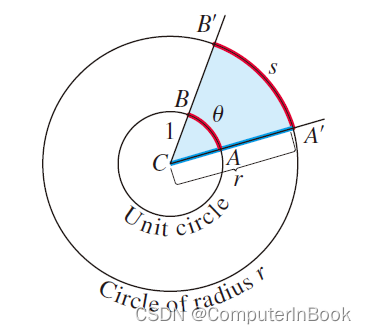
在一个半径为r的圆中，圆心角(central angle)A’CB’的弧度数定义为：圆心角A’CB’ 所对向的弧线段s所包含的“半径单元数(radius units)”。假如，当使用弧度来度量角度时，我们使用θ来表示这个圆心角，则意味着θ=s/r，或者

s = rθ (r以弧度计)

假如圆是一个半径r=1的单位圆，则从以上等式中，我们可以看出，按弧度度量的圆心角θ的大小正好是这个圆心角从单位圆中切下的圆弧段的长度。因为单位圆完整地旋转一周(revolution)对应的角度是360°或者2π弧度，因此，我们可以推出公式

π弧度=180°

因此，1弧度= $\frac{180\degree}{\pi }$ ≈57.3)度(degrees) 或 1度= $\frac{\pi }{180\degree}$

(≈0.017)弧度(radians)

对于xy平面上的一个角，如果它的顶点(vertex)位于(lies at)坐标原点且其初始射线(ray)沿着(lies along)正向的x轴，则称该角处于标准位置(standard position)。

描述逆时针(counterclockwise=counter(逆向)+clock(时针)+wise(前进方式))旋转(rotation)的角度可以是远超2π或360°的任意大角度。类似地，描述顺时针(clockwise)旋转的角度可以有任意大小的负度量。

4.5.2 六种基本的三角函数

sine: $sin \theta =\frac{y}{r}$ , cosecant: $csc \theta =\frac{r}{y}$

cosine: $cos \theta =\frac{x}{r}$ , secant: $sec \theta =\frac{r}{x}$

tangent: $tan\theta =\frac{y}{x}$ ，cotangent: $cot \theta =\frac{x}{y}$

这些定义与当角是锐角(acute)时的直角三角形(right-triangle)的定义一致。

$tan\theta =\frac{sin\theta }{cos\theta }$ ， $cot \theta =\frac{1}{tan\theta }$

$sec\theta =\frac{1}{cos\theta }$ , $csc \theta=\frac{1}{sin \theta}$

可以看出，tan θ和sec θ在x= cos θ =0时是没有定义的。这意味着，假如θ是±π/2，±π/2，……,等等时，它们是没有定义的。类似地，对于使y=0的θ值,即θ=0，±π，±2π，……，等等时，cot θ和csc θ是没有定义的。

关于这几个概念的由来：

(1) sine[saɪn] n. 中文泽为“正弦”(类似于拉弓箭的弓弦，古人称直角三角形的斜边为弦，角度正对面的边与弦的比值,由此得名，实则上正弦是“半弦”，因为与圆有两个交点的线条称为弦，而这里的的“正弦”只是这根弦的一半长)。三个基础三角函数之一(trigonometry),始于1590年(出现在Thomas Fale的书<<Horologiographia, the Art of Dialling>>(钟表，转盘的艺术)中,这本书是用拉丁文语的；Thomas Fale是一位英国数学家，这本书中讲述了诸多三角函数问题。) “sine”这个词来自拉丁语“sinus”，词义为“fold in a garment, bend, curve, bosom(衣服上的折皱，弯曲，曲线，内部)”，参见sinus。拉丁单词“sine”在12世纪中期开始使用，它来自Cremona的 Gherardo对阿拉伯几何教材中古拉丁语转录本，在转录本中，它将阿拉伯语“jiba”(词义为“chord of an arc, sine(弧的弦、正弦)”)( “jiba”这个词来自“Sanskrit(梵文)”的词“jya”，其词义为“bowstring(弓弦)”)翻译成了“sine”，它混淆了词“jiba”和“jaib(bundle, bosom, fold in a garment(束、里面、衣服中的褶皱))”。

(2) cosine[ˈkəʊsaɪn] n. 中文译为“余弦”。三角函数的三个基础函数之一，始于1630年代，“co.sinus”的缩略形式，中古拉丁语“complementi sinus(补角正弦)”(complement + sine)的缩写形式。这个术语是在1620年代由英语数学家Edmund Gunter在拉丁语中使用。因此，“余弦”在数学意义上可以说“补角(相对于90度角而言)的正弦”，这个“余”应该理解为“补角”，“即补角的正弦”。

(3) tangent[ˈtændʒənt] n.三个基础三角函数之一，始于形容词的“tangent”，中文译为“正切”。形容词的“tangent”始于1590年代，词义为“meeting at a point without intersecting(在某一个点接触而不相交,即只与圆有一个交点，也就是一条线与圆“相切”了)”,来自拉丁语“tangentem ”(主格“tangens”)，“ tangere”(“to touch(接触)”)的现在分词。是由丹麦数学家Thomas Fincke在他的著作<< Geomietria Rotundi >>(圆的几何，1583年)中第一次使用。

(4) cotangent [kəʊˈtændʒ(ə)nt] n. 在三角函数中，词义为“the tangent of the complement of a given angle(已知角度的补角的正切)”，“co. tangent”的缩略形式，“complement + tangent”的缩写形式。

(5) secant[ˈsiːkənt] n. 基本三角函数之一，始于1590年代，来自拉丁语“secantem ”(其主格为“secans”),词义为“a cutting(切割)”,“secare”(“to cut(切割)”)的现在分词形式。是由丹麦数学家Thomas Fincke在他的著作<< Geomietria Rotundi >>(圆的几何，1583年)中第一次使用。因线条与圆相割而得名。