---

前言

手撕排序算法第五篇：堆排序！
从本篇文章开始，我会介绍并分析常见的几种排序，例如像插入排序，冒泡排序，希尔排序，选择排序，快速排序，堆排序，归并排序等等！
这篇文章我先来给大家手撕一下堆排序！

大家可以点下面的链接去阅读其他的排序算法：
C语言手撕排序算法

---

正文开始！

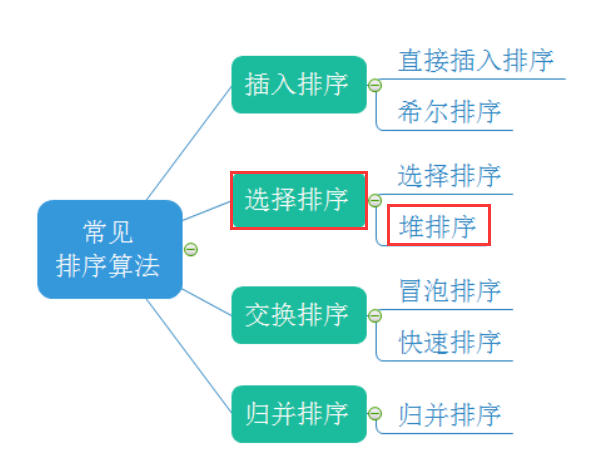
一、常见的排序算法

二、堆的概念及结构

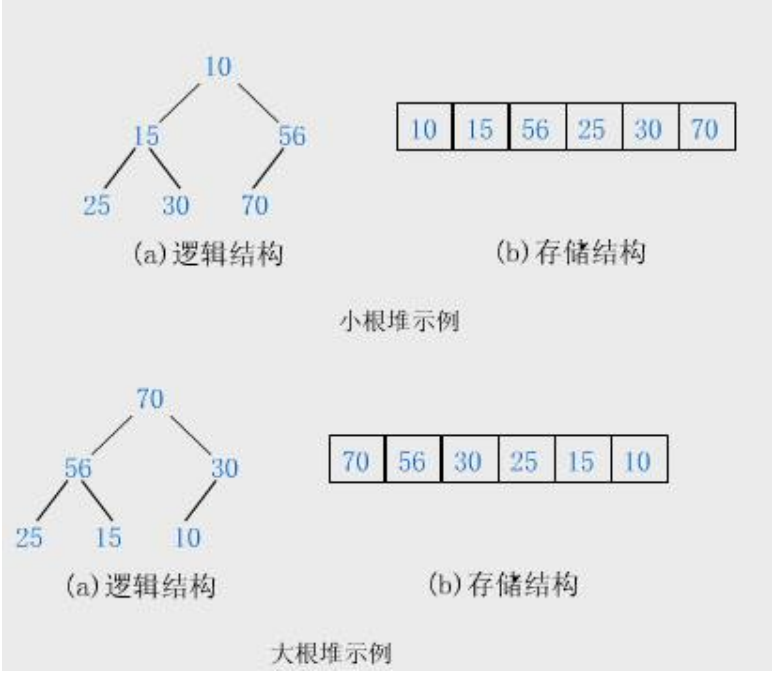
如果有一个关键码的集合K={k0,k1,k2,…,kn-1},把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中，并满足：K_i <=K_2*i+2且K_i<=K_2*i+2(K_i>=K_2*i+1且K_i>=K_2*i+2)其中i=0,1,2,3…,则称之为小堆(大堆)。将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。

堆的性质：

• 堆中某个节点的值总是不大于或不小于其父节点的值；
• 堆总是一颗完全二叉树。

三、堆的实现

3.1 堆的插入

先插入一个10到数组中，然后进行向上调整算法，直到满足堆的性质。

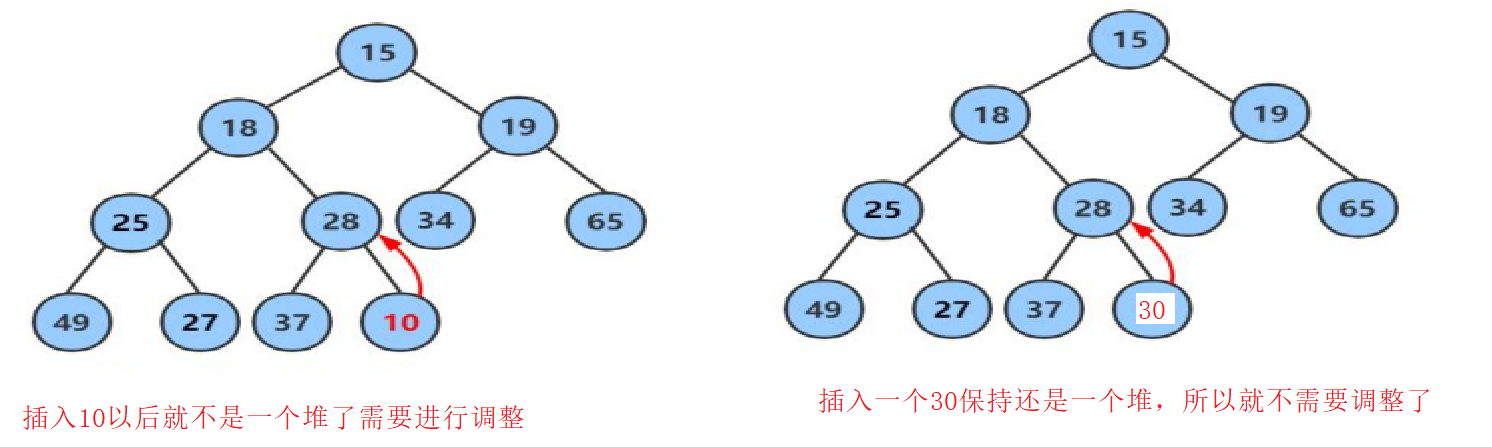
针对插入10之后我们调整来进行分析。

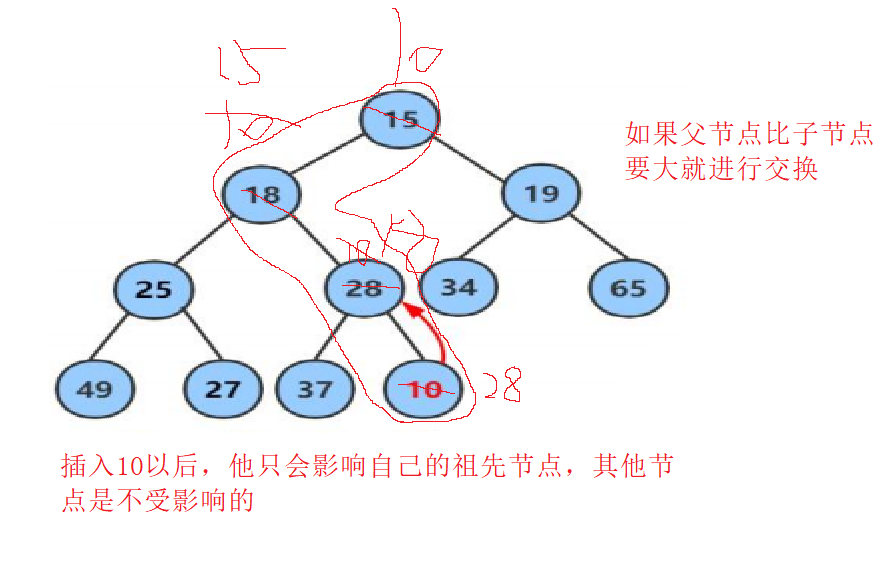
有可能交换到中间满足堆的性质就停止交换了。

void AdjustUp(int* a,size_t child)
{
	size_t parent = (child - 1) / 2;
	while (child>0)
	{
		if (a[child]<a[parent])
		{
			Swap(&a[parent],&a[child]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

算法逻辑是二叉树，物理上操作的是数组中的数据。

3.2 堆的删除

挪动数据覆盖根的位置的数据删除

1. 挪动数据是O(n)。
2. 堆结构破坏了，分子间的关系就全乱了。

所以上面的方法是不可取的。

接下来讲一讲实际操作，如下图所示。

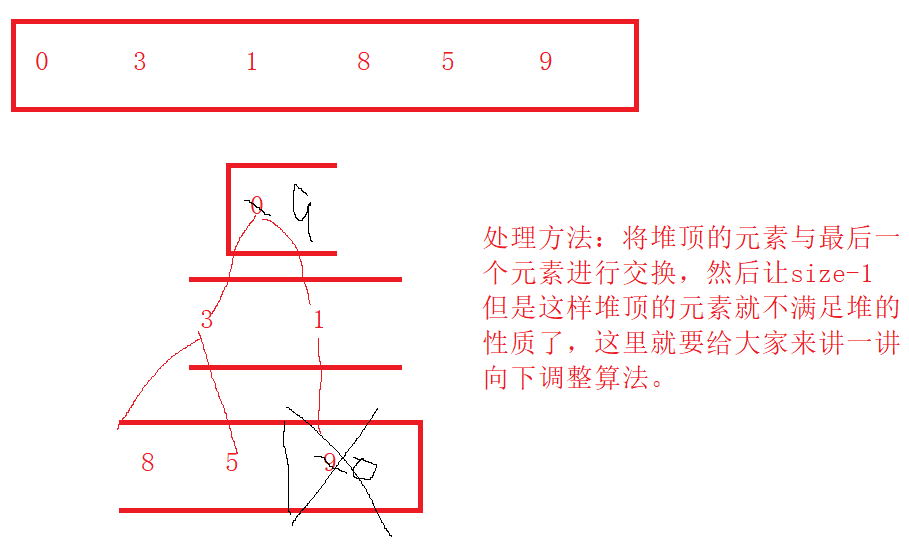
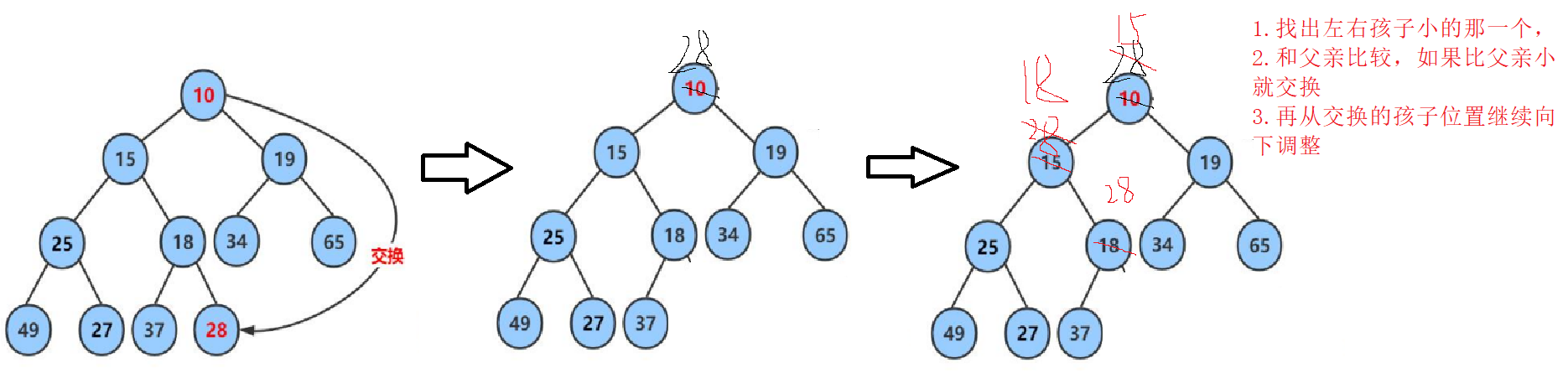
代码实现

void AdjustDown(int* a,size_t size,size_t root)
{
	size_t parent = root;
	size_t child = parent * 2+1;
	while (child < size)
	{
		//选出左右孩子中小的哪一个 
		if (child + 1 < size && a[child + 1] > a[child])
		{
			child++;
		}
		//2.如果孩子小于父亲，则交换，并继续向下调整。
		if (a[child] < a[parent])
		{
			Swap(&a[child],&a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
}

四、堆排序

4.1 向上调整建堆

	//向下调整建堆
	for (int i = 1; i < n; ++i)
	{
		AdjustUp(a,i);
	}

4.2 向下调整建堆

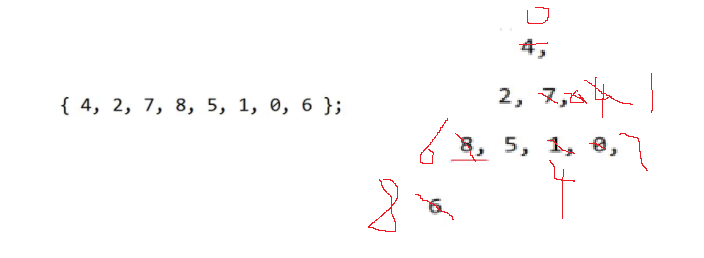
	//向上调整建堆
	for (int i = (n - 1 - 1) / 2; i >= 0; --i)
	{
		AdjustDown(a,n,i);
	}

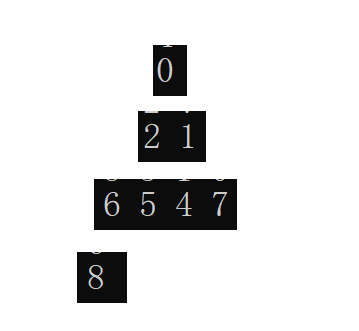
我们可以发现向上调整建堆和向下调整建堆出来的堆是不一样的。

4.3 建堆的时间复杂度

因为堆是完全二叉树，而满二叉树也是完全二叉树，此处为了简化使用满二叉树来证明(时间复杂度本来看就是近似值，多几个节点不影响最终的结果)。

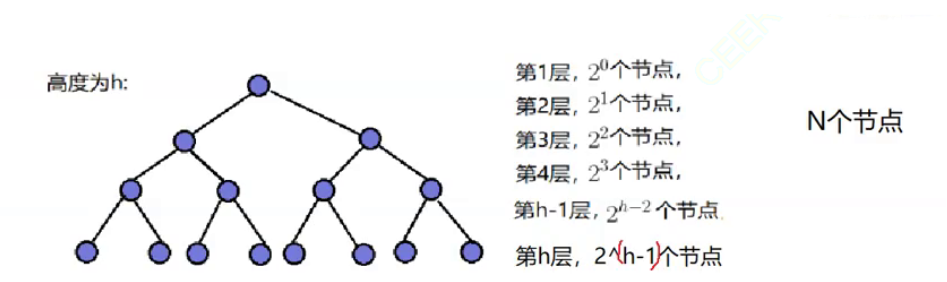
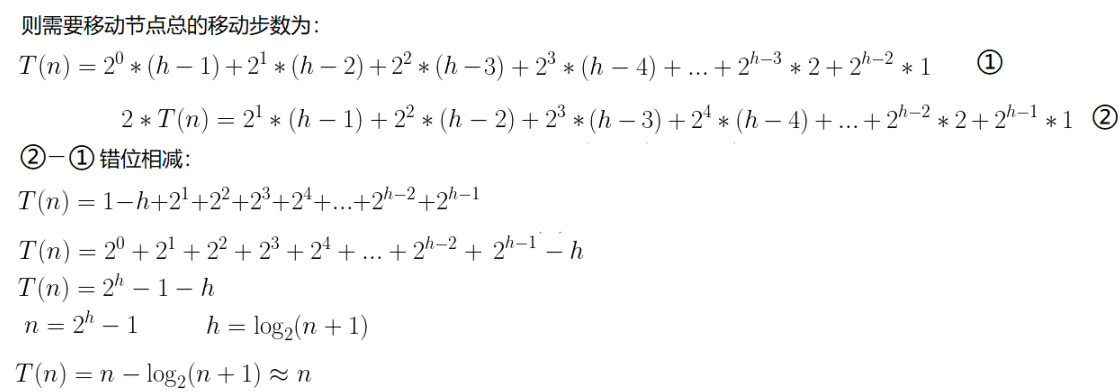因此：建堆的时间复杂度为O(N)。

4.4 堆排序

如果升序建小堆，最小的数已经在堆顶,剩下的数关系打乱,需要重新建堆,建堆最好也要O(N)，再选出次小的,不断建堆选数,如果这样,还不如直接遍历选数！！因此升序要建大堆！！利用删除的思想来玩。

过程：

1. 把第一个数和最后一个数交换，由于是大堆，堆顶的数据一定是最大的数据。和最后一个数交换后，最大的数据就到了最后一个。

2. 再对前N-1个数进行向下调整建立新的大堆，次大的数放在了堆顶，我们再让堆顶的元素和最后一个元素交换（这个最后一个不是数组的最后一个，是堆中的最后一个，使用end进行控制）。

3. 当end到0的时候，说明已经排完了。

void AdjustUp(int* a,size_t child)
{
	size_t parent = (child - 1) / 2;
	while (child>0)
	{
		if (a[child]>a[parent])
		{
			Swap(&a[parent],&a[child]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}
void AdjustDown(int* a,size_t size,size_t root)
{
	size_t parent = root;
	size_t child = parent * 2+1;
	while (child < size)
	{
		//选出左右孩子中小的哪一个 
		if (child + 1 < size && a[child + 1] > a[child])
		{
			child++;
		}
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
//升序
void HeapSort(int* a, int n)
{
	向下调整建堆
	//for (int i = 1; i < n; ++i)
	//{
	//	AdjustUp(a,i);
	//}
	
	//向上调整建堆
	for (int i = (n - 1 - 1/*最后一个非叶子节点*/) / 2; i >= 0; --i)
	{
		AdjustDown(a,n,i);
	}
	//升序排列建大堆
	//找出堆顶元素放入最后一个位置，就是把最大值放到最后一个位置。
	//然后循环下去
	size_t end = n - 1;
	while (end>0)
	{
		Swap(&a[0],&a[end]);
		AdjustDown(a,end,0);
		--end;
	}
}
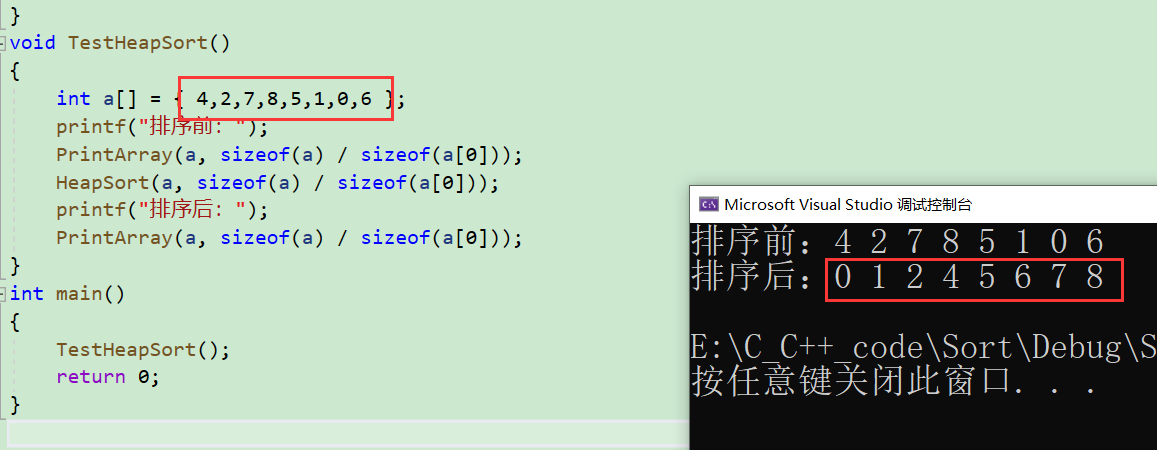
void TestHeapSort()
{
	int a[] = { 4,2,7,8,5,1,0,6 };
	printf("排序前：");
	PrintArray(a, sizeof(a) / sizeof(a[0]));
	HeapSort(a, sizeof(a) / sizeof(a[0]));
	printf("排序后：");
	PrintArray(a, sizeof(a) / sizeof(a[0]));
}
int main()
{
	TestHeapSort();
	return 0;
}

五、堆排序的特性

堆排序最重要的是升序要建大堆，逆序排列要建小堆。

1. 时间复杂度O(NlogN)。
2. 空间复杂度为O(1)。
3. 稳定性：不稳定。

---

（本章完！）