贪心

将至少连续 $K$ 个 $1$ 放在一起。首先考虑他们是相邻着放在一起的，然后考虑性质 : 设相邻摆放后，起始 $1$ 的位置是 $mid$ ，对于每个 $1$ 的位置 $a_i$ ，它需要被摆放的位置是 $a_{mid}+i$ 。考虑一个等价代换，令 $a_i^{{}^{\prime }}=a_i-i$ ，那么 $a_i^{{}^{\prime }}$ 到 $a_{mid}$ 的距离等于 $a_i$ 到 $a_{mid}+i$ 的距离。这一步固定了待求距离的点。

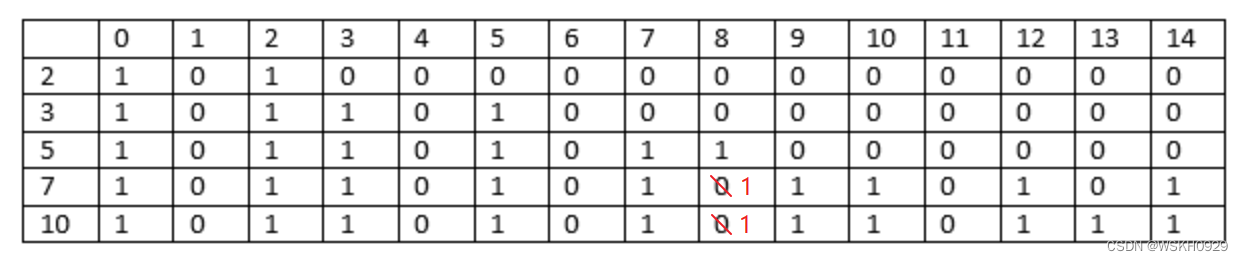
记录所有 $1$ 位置，存于数组 $a$ ，每次考虑 $K$ 个连续的 $1$ ，即 $R-L+1=K$ 。可以证明，要使距离之和最小，只要取中间点即可 (贪心货仓选址)。

先分段讨论，对于左端，距离之和有 : $(a_{mid}-a_L)+(a_{mid}-a_{L+1})+\cdots +(a_{mid}-a_{mid-1})=a_{mid}\times (mid-L)-(S_{mid}-S_{L-1})$ 。其中 $S$ 是前缀和数组。由连续项，想到前缀和。

对于左端，距离之和有 : $(a_{mid+1}-a_{mid})+(a_{mid+2}-a_{mid})+\cdots +(a_R-a_{mid})=(S_R-S_{mid})-a_{mid}\times (R-mid)$ 。

综上，距离之和 $a_{mid}\times (2\times mid-r-l)+s_r-s_{mid}-s_{mid-1}+s_{l-1})$

class Solution {
public:
    int minMoves(vector<int>& nums, int k) {
        vector<int> a;
        for(int i = 0 ;i< nums.size();i++)
            if(nums[i])
                a.push_back(i-a.size());
        int n = a.size();
        int s[n+1];
        for(int i = 1;i<=n;i++)
            s[i] = s[i-1]+a[i-1];
        int ans = INT_MAX ;
        for(int l = 1;l<=n-k+1;l++){
            int r = l + k - 1;
            int mid = (l+r)>>1;
            ans = min(ans,a[mid-1]*(2*mid-r-l) + s[r] - s[mid] - s[mid-1] + s[l-1]);
            //由于求了前缀和，a对应的下标要左移1.
        }
        return ans;
    }
};

1. 时间复杂度 : $O(n)$ ， $n$ 是数字总数，一次遍历找 $1$ ，构造前缀和，遍历 $1$ 的时间复杂度 $O(n)$ 。
2. 空间复杂度 : $O(n)$ ， 存储 $1$ ，前缀和的空间复杂度 $O(n)$ 。

AC

致语

• 理解思路很重要
• 读者有问题请留言，清墨看到就会回复的。