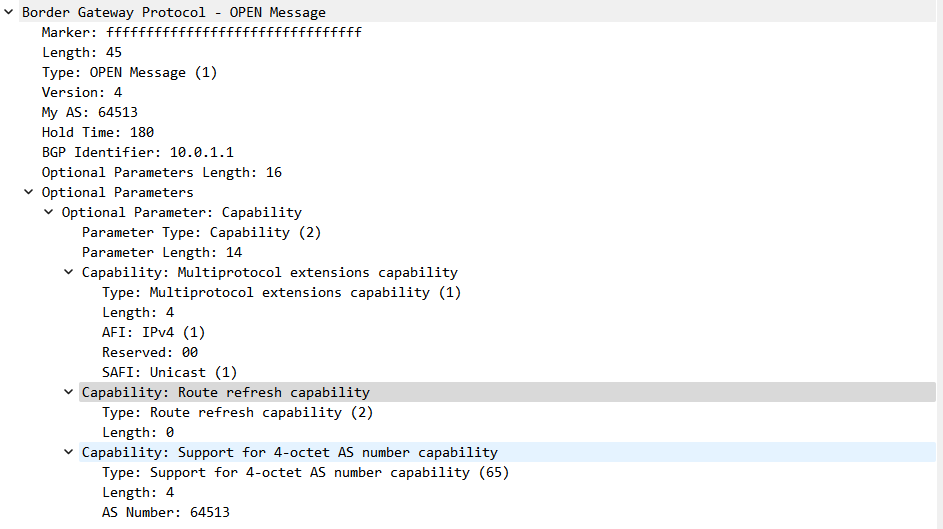
近年来,软件行业发展迅速,软件产品的质量成为用户关注的焦点。而软件的质量评估往往需要依赖专业的第三方测评机构,为了更好地了解软件测试环境对产品质量的重要性,小编整理了以下简析:
一、良好的测试环境对软件产品起到的作用
1、为软件产品提供一个真实、稳定的运行场景,模拟用户的使用情况,为开发人员提供准确的反馈信息。
2、有效地发现和解决软件产品中的潜在问题和漏洞,确保软件的安全性和稳定性。
3、提高软件产品的兼容性和性能,确保在不同平台和设备上都能正常运行。
二、如何搭建一个良好的测试环境?
1、准备强劲的测试服务器:确保软件在真实环境下的运行效果
2、搭建完备的测试数据库:用以存储和管理测试数据,同时保证测试数据的安全性和可靠性
3、配置适合的测试工具和环境:例如性能测试工具、自动化测试工具等
4、保证测试环境与实际使用环境接近:包括操作系统、数据库版本、网络环境等
5、合理规划和分配测试资源:确保测试人员和测试工具的充分利用
6、制定详细的测试计划和测试用例:确保全面、系统地进行测试
综上所述,在软件质量评估中,良好的测试环境起到了至关重要的作用。只有建立一个真实、稳定且完备的测试环境,才能充分发挥软件产品的潜力,提高软件的可靠性和安全性。