数据结构——二叉树线索化遍历(前中后序遍历)

news2024/11/15 21:38:33

二叉树线索化

线索化概念：

为什么要转换为线索化

        二叉树线索化是一种将普通二叉树转换为具有特殊线索（指向前驱和后继节点）的二叉树的过程。这种线索化的目的是为了提高对二叉树的遍历效率，特别是在不使用递归或栈的情况下进行遍历。

        将二叉树线索化的主要目的是为了提高对二叉树的遍历效率以及节省存储空间。线索化使得在不使用递归或栈的情况下可以更快速地进行遍历，特别是在特定顺序的遍历时，如前序、中序或后序遍历。  

  1. 提高遍历效率：线索化后，可以在常量时间内找到节点的前驱和后继节点，从而实现更高效的遍历。这对于需要频繁遍历大型二叉树或需要在树的中间部分执行插入和删除操作时特别有用。

  2. 无需递归或栈：线索化的二叉树允许你在遍历时省去递归或栈的开销，因为你可以沿着线索直接访问节点的前驱和后继，从而降低了内存和时间复杂度。

  3. 节省存储空间：线索化可以用较少的额外存储空间来实现。通常，只需为每个节点添加一个或两个指针来存储线索信息，而不需要额外的数据结构（如堆栈）来辅助遍历。

  4. 支持双向遍历：线索化的二叉树可以支持双向遍历，即可以在给定节点的前向和后向方向上遍历树。这在某些应用中很有用，例如双向链表的操作。

  5. 节省计算资源：在某些特定的应用场景中，通过线索化可以避免重复计算，因为可以直接访问前驱和后继节点，而无需再次搜索或遍历

树的遍历

        先给定一棵树，然后对他进行每种遍历：

        前序遍历：

        前序遍历，就是先遍历根节点在遍历左子树，在遍历右子树；

        他的顺序就是：根节点->左子树->右子树

        根据递归先遍历了根节点，然后递归左子树，回溯后在进行遍历右子树的一个过程；

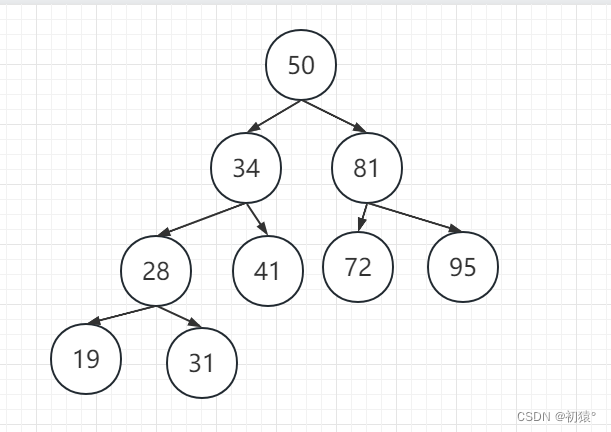
        例如上图开始前序遍历：

        遍历根节点50，然后递归左子树，34，现在把34看为根节点继续递归左子树，28，然后把28看作根节点，继续遍历左子树，19，然后把19看为根节点继续遍历，然后左子树为空，开始回溯，回溯到19，遍历右子树也为空，继续回溯到结点28，遍历右子树，31；然后通过这种思想一直进行遍历最总遍历完整棵子树；

        前序遍历结果：50，34，28，19，31，41，81，72，95

        中序遍历：

        顺序是：左子树->根节点->右子树

        其实在理解了前序遍历后，中序遍历也差不多的，刚才是先记录了根节点，现在开始，先一直递归遍历左子树，递归到没有左子树的时开始记录，比如上图递归到19，然后回溯，28，遍历右子树31，回溯34，遍历右子树41，回溯50，遍历右子树；然后最终的结果就是：

        19，28，31，34，41，50，72，81，95；

        中序遍历就是，找到子树的最左边的那个结点，然后回溯到它的父节点，然后遍历他父节点的右子树，然后到右子树中又去找它的最左的结点，这样一直经过这样的操作，最终完成中序遍历。

        后序遍历：

        顺序是：左子树->右子树->根节点

        先是左子树，那就先找到左子树中的最左边的结点，19，然后回溯，遍历右子树，然后再右子树中找最左边的结点，31，回溯28，然后在回溯；这样的一个过程；

        最终结果就是：

        19，31，28，41，34，72，95，81，50

        后序遍历，看着比中序和后序遍历难理解，其实只要懂得了递归回溯的那个过程，就思路回非常的清晰；然后大概的过程就是先遍历左子树，找到左子树中最左边的结点，回溯，然后遍历右子树，遍历右子树的过程也是先遍历右子树中的左子树，然后再进行遍历右子树的右子树，最后来遍历他们的根节点；

        3种遍历的代码实现：  


void pre_orderNode(Node *root) {前序
    if (!root) return ;
    printf("%d ", root->data);//先输出根节点
    pre_orderNode(root->lchild);//遍历左子树
    pre_orderNode(root->rchild);//遍历右子树
    return ;
}


void in_orderNode(Node *root) {中序
    if (!root) return ;
    in_orderNode(root->lchild);//先遍历左子树
    printf("%d ", root->data);//在打印根节点的值
    in_orderNode(root->rchild);//在遍历右子树
    return ;
}

void post_orderNode(Node *root) {后序
    if (!root) return ;
    post_orderNode(root->lchild);//先遍历左子树
    post_orderNode(root->rchild);//在遍历右子树
    printf("%d ", root->data);//最终打印根节点值
    return ;
}

        可以去理解一下代码，尝试在纸上或者脑子里执行以下代码，模拟运行以下；

二叉树前序线索化：

        

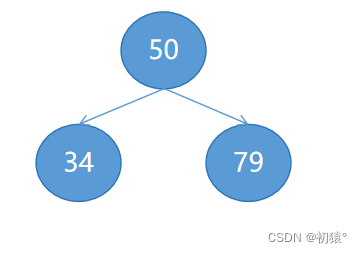
        如图上图一个简单的二叉树，现在是将这个二叉树进行前序线索化，那么前序遍历的顺序是根节点->左子树->右子树;

        那么根节点就应该在条线的头部，然后再去遍历左子树和右子树，那么这个数的前序遍历结果是50，34，79；

        

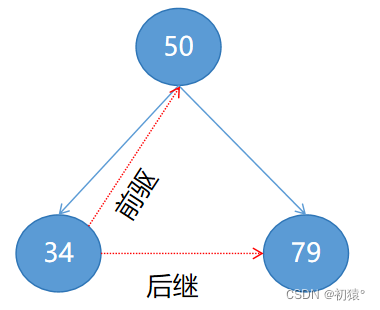
        那么就可以将二叉树样来看，50是34的前驱，79是34的后继，前驱就是在遍历在他前面的，后继就是在他后面遍历的；

        现在我们将每个结点的指向两个子孩子指针改变为指向他的前驱和后继：

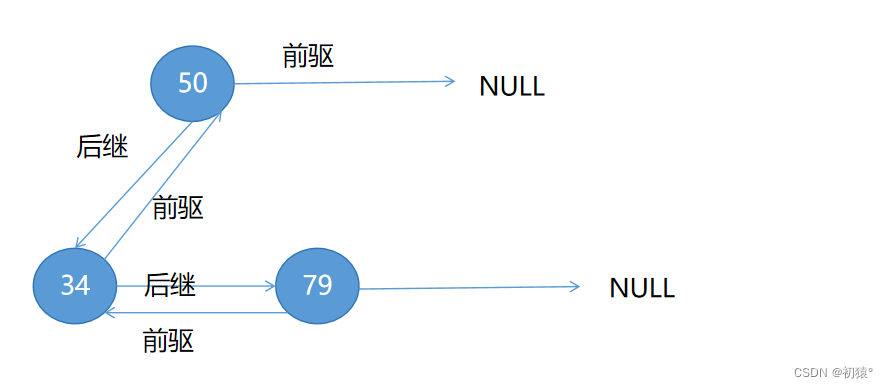
        通过这样的转换，那这棵树就转换为一条双向链表了：

        其中会发下50和79的会右一颗子树指向NULL，那么就需要用一个变量来记录，他是否右前驱或者后继；

        就是这样的一个转换，也证明了概念种的节省空间，不用递归遍历，可以双向遍历，提高了遍历效率；

        下面是代码实现：

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

#define NORMAL 0
#define THRENA 1 

//这里左儿子记录前驱，右儿子记录后继
typedef struct Node {
    int val, ltag, rtag;//val结点的值，ltag记录是否有前驱,rtag记录是否有后继
    struct Node *lchild, *rchild;
} Node;

Node *getNewNode(int val) {//获取新的结点
    Node *root = (Node *)malloc(sizeof(Node));
    root->lchild = root->rchild = NULL;
    root->rtag = root->ltag = NORMAL;//NORMAL表示还未有前驱或后继
    root->val = val;
    return root;
}

Node *insert(Node *root, int val) {//添加结点，组成普通的二叉树
    if (!root) return getNewNode(val);
    if (root->val == val) return root;
    if (root->val > val) root->lchild = insert(root->lchild, val);
    else root->rchild = insert(root->rchild, val);
    return root;
}

void build_Thread(Node *root) {//建立线索化
    if (!root) return ; 
    static Node *pre = NULL;//使用静态变量使得pre值不随程序递归而改变
    Node *left = root->lchild;//记录当前结点左右儿子 
    Node *right = root->rchild;
    if (root->ltag == NORMAL) {//当前结点没有前驱结点
        root->lchild = pre;//给当前结点赋值前驱结点
        root->ltag = THRENA;//标记有前驱结点
    }
    if (pre && pre->rtag == NORMAL) {//如果它的前驱结点没有后继，并且前驱结点不为NULL
        pre->rchild = root;//将前驱结点的后继附上当前结点
        pre->rtag = THRENA;//标记前驱结点有后继了
    }
    pre = root;//pre等于当前递归的结点
    build_Thread(left);//递归左子树
    build_Thread(right);//在递归右子树
    return ;
}

void output(Node *root) {//遍历线索化二叉树
    if (!root) return ;
    Node *p = root;
    while (p) {
        printf("%d ", p->val);
        if (p->rtag == THRENA) p = p->rchild;//说明当前结点有后继直接往右节点也就是后继结点继续遍历
        else if (p->rtag == NORMAL) break;//如果当前结点没有后继结束遍历 
    }
    return ;
}


void preface(Node *root) {//普通前序递归遍历
    if (!root) return ;
    printf("%d ", root->val);
    if (root->ltag == NORMAL) preface(root->lchild);
    if (root->rtag == NORMAL) preface(root->rchild);
    return ;
}

void clearNode(Node *root) {//回收空间
    if (!root) return ;
    if (root->ltag == NORMAL) clearNode(root->lchild);
    if (root->rtag == NORMAL) clearNode(root->rchild);
    free(root);
    return ;
}


int main() {
    srand(time(0));//获取当期计算时间，获取随机数
    Node *root = NULL;
    for (int i = 0; i < 10; i++) {
        int val = rand() % 100;
        root = insert(root, val);
    }
    preface(root);//先打印普通前序遍历
    putchar(10);//换行
    build_Thread(root);//建立线索化
    output(root);//输出前序线索化
    putchar(10);
    clearNode(root);
    return 0;
}

二叉树中序线索化：

       

        中序遍历顺序：左子树->根节点->右子树

        那么结果借是34，50，79

        转换线索化，那么34就是50的前驱，50就是34的后继；和前序遍历的是一样的；

        直接来看代码实现：

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define NORMAL 0 //表示没有
#define THRENA 1 //表示有
//这里左儿子记录前驱，右儿子记录后继
typedef struct Node {
    int val, ltag, rtag;///val结点的值，ltag记录是否有前驱,rtag记录是否有后继
    struct Node *lchild, *rchild; 
} Node;

Node *getNewNode(int val) {///获取新的结点
    Node *p = (Node *)malloc(sizeof(Node));
    p->val = val;
    p->lchild = p->rchild = NULL;
    p->ltag = p->rtag = NORMAL;//NORMAL表示还未有前驱或后继
    return p;
}

Node *insert(Node *root, int val) {//添加结点，组成普通的二叉树
    if (!root) return getNewNode(val);
    if (root->val == val) return root;
    if (root->val > val) root->lchild = insert(root->lchild, val);
    else root->rchild = insert(root->rchild, val);
    return root;
}



void in_order(Node *root) {//普通递归中序遍历
    if (!root) return ;
    if (root->ltag == NORMAL) in_order(root->lchild);
    printf("%d ", root->val);
    if (root->rtag == NORMAL) in_order(root->rchild);
    return ;
}

void build_Thread(Node *root) {//建立线索化
    if (!root) return ;
    static Node *pre = NULL;//使用静态变量使得pre值不随函数递归过程改变而改变
    build_Thread(root->lchild);//由于是中序遍历，先递归到最左结点
    //中间过程就是想当于根节点
    if (root->ltag = NORMAL) {
        root->lchild = pre;
        root->ltag = THRENA;
    }
    if (pre && pre->rchild == NORMAL) {
        pre->rchild = root; 
        pre->rtag = THRENA;
    }
    pre = root;
    build_Thread(root->rchild);//然后再遍历右子树
    return ;
}

Node *most_left(Node *root) {//找到最左结点
    Node *temp = root;
    while (temp && temp->ltag == NORMAL && temp->lchild != NULL) temp = temp->lchild;
    return temp;
}

void output(Node *root) {
    if (!root) ;
    Node *p = most_left(root);//从最左结点开始遍历
    while (p) {
        printf("%d ", p->val);
        if (p->rtag == THRENA) p = p->rchild;//如果后继存在进行遍历后继
        else p = most_left(p->rchild);//找到右子树的最左结点继续遍历
    }
    return ;
}

void clear(Node *root) {
    if (!root) return ;
    if (root->ltag == NORMAL) clear(root->lchild);
    if (root->rtag == NORMAL) clear(root->rchild);
    free(root);
    return ;
}

int main() {
    srand(time(0));    
    Node *root = NULL;
    for (int i = 0; i < 10; i++) {
        int val = rand() % 100;
        root = insert(root, val);
    }
    in_order(root);
    putchar(10);
    build_Thread(root);
    output(root);
    putchar(10);
    clear(root);
    return 0;
}

        二叉树后序线索化：

        直接上代码演示，如果前面两种你都弄懂了那么，后序理解起来也非常容易：

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

#define NORMAL 0
#define THRENA 1 


typedef struct Node {
    int val, ltag, rtag;
    struct Node *lchild, *rchild;
} Node;

Node *getNewNode(int val) {
    Node *root = (Node *)malloc(sizeof(Node));
    root->lchild = root->rchild = NULL;
    root->rtag = root->ltag = NORMAL;
    root->val = val;
    return root;
}

Node *insert(Node *root, int val) {
    if (!root) return getNewNode(val);
    if (root->val == val) return root;
    if (root->val > val) root->lchild = insert(root->lchild, val);
    else root->rchild = insert(root->rchild, val);
    return root;
}

void build_Thread(Node *root) {
    if (!root) return ; 
    static Node *pre = NULL;
    build_Thread(root->lchild);
    build_Thread(root->rchild);
    if (root->ltag == NORMAL) {
        root->lchild = pre;
        root->ltag = THRENA;
    }
    if (pre && root->rtag == NORMAL) {
        pre->rchild = root;
        pre->rtag = THRENA;
    }
    pre = root;
    return ;
}

Node *most_left(Node *root) {
    while (root && root->ltag == THRENA && root->lchild) root = root->lchild;
    return root;
}

void output(Node *root) {
    if (!root) return ;
    Node *p = most_left(root);
    while (p) {
        printf("%d ", p->val);
        if (p->rtag == THRENA) p = p->rchild;  
        else if (p->rtag == NORMAL) break;
    }
    return ;
}


void back_order(Node *root) {
    if (!root) return ;
    if (root->ltag == NORMAL) back_order(root->lchild);
    if (root->rtag == NORMAL) back_order(root->rchild);
    printf("%d ", root->val);
    return ;
}

void preface(Node *root) {
    if (!root) return ;
    printf("%d(", root->val);
    if (root->ltag == NORMAL) preface(root->lchild);
    printf(",");
    if (root->rtag == NORMAL) preface(root->rchild);
    printf(")");
    return ;
}

void clearNode(Node *root) {
    if (!root) return ;
    if (root->ltag == NORMAL) clearNode(root->lchild);
    if (root->rtag == NORMAL) clearNode(root->rchild);
    free(root);
    return ;
}


int main() {
    srand(time(0)); 
    Node *root = NULL;
    for (int i = 0; i < 10; i++) {
        int val = rand() % 100;
        root = insert(root, val);
    }
    preface(root);
    putchar(10);
    back_order(root);
    putchar(10);
    build_Thread(root);
    output(root);
    putchar(10);
    clearNode(root);
    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/985545.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

io和进程day03（文件IO、文件属性函数、目录相关函数）

io和进程day03（文件IO、文件属性函数、目录相关函数）

今日任务 代码 #include <stdio.h> #include <string.h> #include <stdlib.h> #include <sys/types.h> #include <sys/stat.h> #include <unistd.h> #include <sys/types.h> #include <pwd.h> #include <dirent.h> #in…
阅读更多...
【管理运筹学】第 7 章 | 图与网络分析（3，最短路问题）

【管理运筹学】第 7 章 | 图与网络分析（3，最短路问题）

文章目录 引言三、最短路问题3.1 最短路问题定义3.2 Dijkstra 算法3.2.1 算法基本依据3.2.2 算法基本思想与步骤 3.3 逐次逼近算法&#xff08;Bellman-Ford 算法&#xff09;3.4 Floyd 算法 写在最后 引言 承接前文&#xff0c;我们来学习图论中另一个经典问题 —— 最短路问…
阅读更多...
解决：使用MySQL Command Line Client时光标不显示的问题

解决：使用MySQL Command Line Client时光标不显示的问题

项目场景&#xff1a; 在使用MySQL Command Line Client时&#xff0c;有时候光标会不显示出来&#xff0c;就像下面的图片显示一样。 问题描述&#xff1a; 光标会不显示出来。 解决方案&#xff1a;​​​​​​​ 1.首先将输入法切换到中文输入法&#xff0c;然后随便打出一…
阅读更多...
（2023，Diffusion 稳健性 攻击）稳定扩散模型是不稳定的

（2023，Diffusion 稳健性 攻击）稳定扩散模型是不稳定的

Stable Diffusion is Unstable 公众号&#xff1a;EDPJ&#xff08;添加 VX&#xff1a;CV_EDPJ 进交流群获取资料&#xff09; 目录 0. 摘要 1. 简介 2. 相关工作 2.1 扩散模型 2.2 文本到图像模型的缺陷 3. 基础 4. 稳定扩散模型的缺陷 4.1 生成速度的变化 4.…
阅读更多...
介绍PHP

介绍PHP

PHP是一种流行的服务器端编程语言&#xff0c;用于开发Web应用程序。它是一种开源的编程语言&#xff0c;具有易学易用的语法和强大的功能。PHP支持在服务器上运行的动态网页和Web应用程序的快速开发。 PHP可以与HTML标记语言结合使用&#xff0c;从而能够生成动态的Web页面&a…
阅读更多...
Java实践-物联网loT入门-MQTT传输协议

Java实践-物联网loT入门-MQTT传输协议

前言 MQTT是一个极其轻量级的发布/订阅消息传输协议,适用于网络带宽较低的场合. 它通过一个代理服务器&#xff08;broker&#xff09;&#xff0c;任何一个客户端&#xff08;client&#xff09;都可以订阅或者发布某个主题的消息&#xff0c;然后订阅了该主题的客户端则会收…
阅读更多...
红米note5 拆金属外壳

红米note5 拆金属外壳

红米note5 拆金属外壳 卡扣式 外壳 屏幕 先拿下来&#xff0c;sim卡的那个卡座。 贴边&#xff0c;到这个卡扣的地方&#xff0c;用工具翘一下&#xff0c;然后下一个卡扣的地方翘一下&#xff0c;然后慢慢的整个的拿下来。 别硬翘&#xff0c;小刀的刀尖&#xff0c;容易给…
阅读更多...
jeesite自定义数据字典，自定义字典表，自带树选择数据源(保姆级图文教程)

jeesite自定义数据字典，自定义字典表，自带树选择数据源(保姆级图文教程)

文章目录 前言一、框架自带树字典表如何使用二、自定义表作为字典表1. 下拉选项使用自建表作为字典表。实际效果框架示例实际开发代码总结前言 项目开发中字典表如果不满足实际需求，比如使用自己的表作为字典，系统自带字典表树如何使用等问题进行总结记录。 一、框架自带树字…
阅读更多...
端口扫描-安全体系-网络安全技术和协议

端口扫描-安全体系-网络安全技术和协议

端口扫描-安全体系-网络安全技术和协议 端口扫描信息安全的保证体系和评估方法网络安全技术网络攻击和威胁(重要)网络安全协议 端口扫描 全TCP连接:三次握手 半打开式扫描:前两次握手 FIN扫描:不用建立TCP连接 第三方扫描: 拒绝服务攻击有: 同步包风暴ICMP攻击SNMP攻击 都是修改…
阅读更多...
卡牌类游戏推荐，卡牌类三国手游排行榜

卡牌类游戏推荐，卡牌类三国手游排行榜

以下是小编要推荐给大家的关于卡牌类三国手游排行榜的内容。这里有来自各个历史阶段的名将和美女&#xff0c;让你体验最真实的三国战役。你可以将各种战略思维运用到其中&#xff0c;感受步步为营的喜悦&#xff0c;最终赢得战火纷飞的三国&#xff0c;如果想了解每个游戏的具…
阅读更多...
c高级day2 linux指令的补充和shell脚本

c高级day2 linux指令的补充和shell脚本

思维导图 写一个1.sh脚本&#xff0c;将以下内容放到脚本中&#xff1a; 在家目录下创建目录文件&#xff0c;dir 在dir下创建dir1和dir2 把当前目录下的所有文件拷贝到dir1中&#xff0c; 把当前目录下的所有脚本文件拷贝到dir2中 把dir2打包并压缩为dir2.tar.xz 再把di…
阅读更多...
维维数码：网络电视机顶盒怎么样？口碑电视机顶盒排行榜

维维数码：网络电视机顶盒怎么样？口碑电视机顶盒排行榜

欢迎各位来到维维数码频道&#xff0c;最近后台收到很多私信咨询我网络电视机顶盒怎么样&#xff0c;值不值得买&#xff1f;当家里是老电视想升级智能电视&#xff0c;或者智能电视使用几年后出现卡顿、资源少、无法下载软件等&#xff0c;只需要买一台网络电视机顶盒就可以解…
阅读更多...
Tomcat环境变量配置教程

Tomcat环境变量配置教程

1、在官网下载并解压Tomcat&#xff0c;记住解压好的目录&#xff0c;后面配置环境需要用到。 官网地址&#xff1a;Apache Tomcat - Welcome! --- 阿帕奇雄猫 - 欢迎&#xff01; 2、右键此电脑&#xff08;我的电脑&#xff09;->属性->高级系统设置->环境变量 3、…
阅读更多...
NoSQL之redis持久化（RDB、AOF）

NoSQL之redis持久化（RDB、AOF）

目录 一、Redis高可用 二、Redis持久化 1、持久化的功能 2、Redis的两种持久化 三、RDB 持久化 1、触发条件 1.1 手动触发 1.2 自动触发 1.3 其它自动触发机制 2、执行流程 3、启动时加载RED文件(恢复) 四、Redis的AOF持久化 1、开启AOF 2、执行流程 2.1 命令追加…
阅读更多...
SSD202D-boot-IO复用功能

SSD202D-boot-IO复用功能

SSD202D-logo分区添加dtb_旋风旋风的博客-CSDN博客 可以参考该博客,当然我为了兼容以前的固件又优化了该思路: 直接把对应的包添加在logo_202d的尾部,这样就不会影响原来的包 这两张就是修改之后的结构,只在尾部追加DTB 其中ABC结构体 //A结构体- (12 size) typedef struc…
阅读更多...
elementPlus + table 树形懒加载 新增，删除，修改 局部刷新

elementPlus + table 树形懒加载 新增，删除，修改 局部刷新

#直接上代码# 1.表格数据 2.数据源 <m-table ref"cTable" v-if"Object.keys(props.tableData).length" :options"props.tableOptions" :data"props.tableData.data" :isLoading"props.tableData.loading" elementLo…
阅读更多...
数据结构与算法（四）：栈与队列

数据结构与算法（四）：栈与队列

栈与队列 我们一般把栈与队列合在一块讨论&#xff0c;因为他们具有相似的性质。 栈&#xff1a;栈是限定仅在表尾进行插入和删除操作的线性表&#xff0c;所以栈又称为后进先出&#xff08;LastIn First Out&#xff09;的线性表&#xff0c;简称LIFO结构。 队列&#xff1…
阅读更多...
【C++二叉树】进阶OJ题

【C++二叉树】进阶OJ题

【C二叉树】进阶OJ题 目录 【C二叉树】进阶OJ题1.二叉树的层序遍历II示例代码解题思路 2.二叉搜索树与双向链表示例代码解题思路 3.从前序与中序遍历序列构造二叉树示例代码解题思路 4.从中序与后序遍历序列构造二叉树示例代码解题思路 5.二叉树的前序遍历&#xff08;非递归迭…
阅读更多...
C++学习笔记--函数重载(2)

C++学习笔记--函数重载(2)

文章目录 1.3、Function Templates Handling1.3.1、Template Argument Deduction1.3.2、Template Argument Substitution 1.4、Overload Resolution1.4.1、Candidate functions1.4.2、Viable functions1.4.3、Tiebreakers 1.5、走一遍完整的流程1.6、Name Mangling1.7、总结 1.…
阅读更多...
SpringCloud-Hystrix 服务降级与熔断

SpringCloud-Hystrix 服务降级与熔断

接上文SpringCloud-Feign 问题描述 为了解决上述情况&#xff0c;SpringCloud提供了Hystrix熔断器组件&#xff0c;如同保险丝。服务降级则不会直接返回错误&#xff0c;而是提供一个补救措施&#xff0c;正常响应给请求者。 1.服务降级 基于借阅管理服务&#xff0c;不开启…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023