一：前言

波士顿房价是机器学习中很常用的一个解决回归问题的数据集

数据统计于1978年，包括506个房价样本，每个样本包括波士顿不同郊区房屋的13种特征信息，

比如：住宅房间数、城镇教师和学生比例等

标签值是每栋房子的房价(千美元)；所以这是一个小型数据集，有506*14维

具体步骤包括有

1.加载数据集并获取有效信息

2.划分训练集和测试集

3.对特征做均值方差归一化

4.建立KNN回归模型并预测

相关属性包括有

No	属性	字段描述
1	CRIM	城镇人均犯罪率
2	ZN	占地面积超过2.5万平方英尺的住宅用地比例
3	INDUS	城镇非零售业务地区的比例
4	CHAS	查尔斯河虚拟变量(=1如果土地在河边；否则是0)
5	NOX	一氧化氮浓度(每1000万份)
6	RM	平均每居民房数
7	AGE	在1940年之前建成的所有者占用单位的比例
8	DIS	与五个波士顿就业中心的加权距离
9	RAD	辐射状公路的可达性指数
10	TAX	每10000美元的全额物业税率
11	PTRATIO	城镇师生比例
12	B	1000(BK-0.63)^2其中Bk是城镇黑人的比例
13	LSTAT	人口中地位较低人群的百分数
14	MEDV	(目标变量/类别属性)以1000美元计算的自有住房的中位数

二：模型预测(KNN算法)

网格模型，超参调优测试

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.neighbors import KNeighborsClassifier, KNeighborsRegressor
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

# 加载数据  鸢尾花load_iris
boston_datasets = load_boston()
# 特征数据
boston_data = boston_datasets['data']
# 标签数据
boston_target = boston_datasets['target']
# 数据集划分
X_train, X_test, y_train, y_test = train_test_split(boston_data, boston_target, test_size=0.3, random_state=6)
knn_model = KNeighborsRegressor()
param_list = [
    {
        "n_neighbors": list(range(1, 18)),
        "p": list(range(1, 26)),
        "weights": ['uniform', 'distance']
    }
]

grid = GridSearchCV(knn_model, param_list, cv=4)
grid.fit(X_train, y_train)
print(grid.best_score_)
print(grid.best_params_)
print(grid.best_estimator_)

0.6163962297065405
{'n_neighbors': 5, 'p': 1, 'weights': 'distance'}
KNeighborsRegressor(p=1, weights='distance')

输出结果如上所示：评分0.61很低

n_neighbors:5

p:1

weights:'distance'

KNN模型预测

# 选择算法 -- 有监督的分类问题
# KNN K近邻算法(近朱者赤近墨者黑)
# 创建算法
knn_model = KNeighborsRegressor(n_neighbors=5, p=1, weights='distance')
# 构建基于训练集的模型
knn_model.fit(X_train, y_train)
# 模型评分
score = knn_model.score(X_test, y_test)
print(score)
# 模型预测
predict_y = knn_model.predict(X_test)
print(predict_y == y_test)

预测结果，不尽人意，模型评分本身就低...

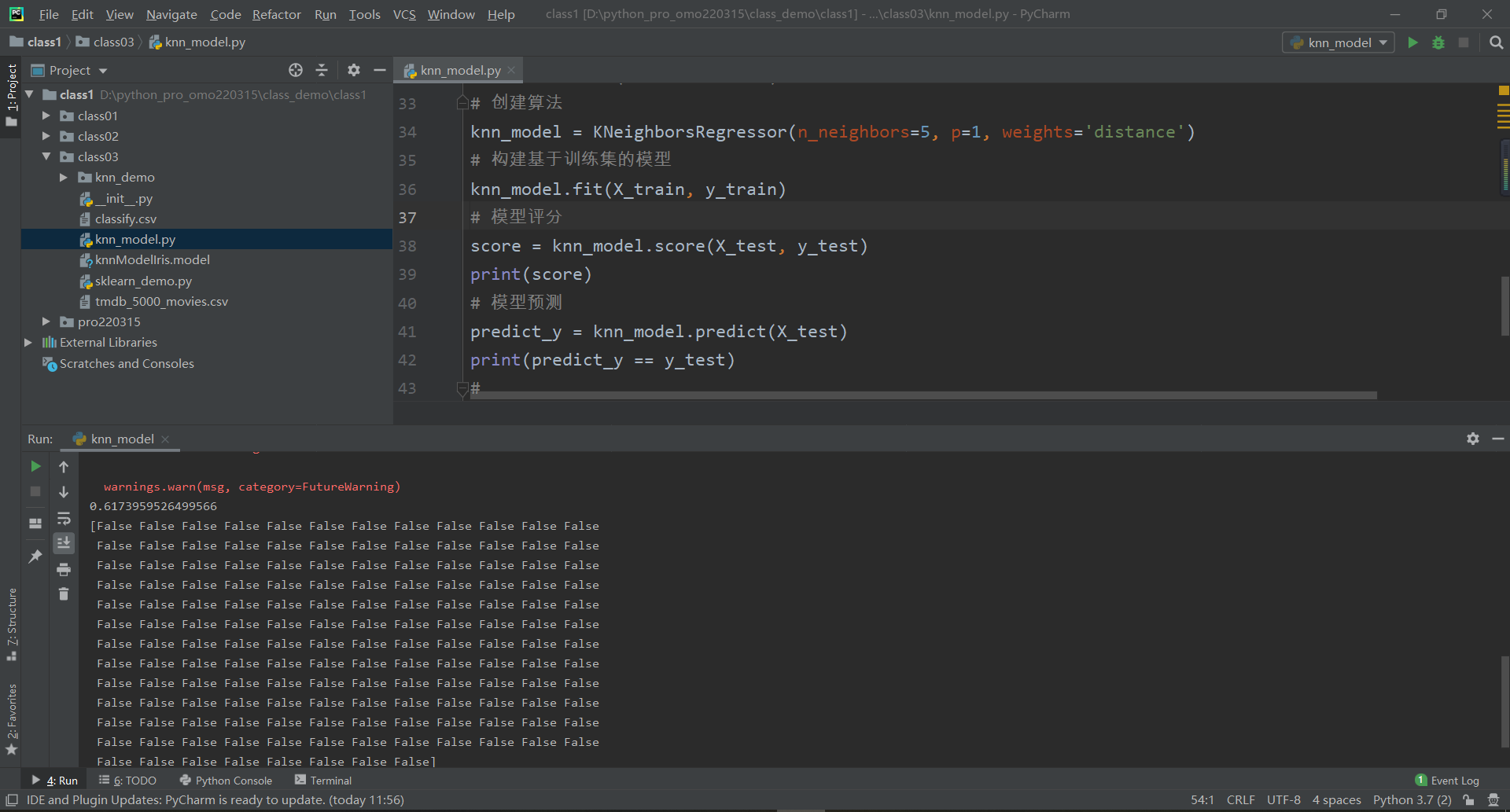
对于回归问题，最好图像查看数据，使用模型预测比对

import matplotlib.pyplot as plt

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.neighbors import KNeighborsClassifier, KNeighborsRegressor
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

# 加载数据  鸢尾花load_iris
boston_datasets = load_boston()
# 特征数据
boston_data = boston_datasets['data']
# 标签数据
boston_target = boston_datasets['target']
# 数据集划分
X_train, X_test, y_train, y_test = train_test_split(boston_data, boston_target, test_size=0.3, random_state=6)
# knn_model = KNeighborsRegressor()
# param_list = [
#     {
#         "n_neighbors": list(range(1, 18)),
#         "p": list(range(1, 26)),
#         "weights": ['uniform', 'distance']
#     }
# ]
#
# grid = GridSearchCV(knn_model, param_list, cv=4)
# grid.fit(X_train, y_train)
# print(grid.best_score_)
# print(grid.best_params_)
# print(grid.best_estimator_)

# 选择算法 -- 有监督的分类问题
# KNN K近邻算法(近朱者赤近墨者黑)
# 创建算法
knn_model = KNeighborsRegressor(n_neighbors=5, p=1, weights='distance')
# 构建基于训练集的模型
knn_model.fit(X_train, y_train)
# 模型评分
score = knn_model.score(X_test, y_test)
# print(score)
# 模型预测
predict_y = knn_model.predict(X_test)
# print(predict_y == y_test)

# 模型预测对比
plt.plot(y_test, label='True')
plt.plot(predict_y, 'r:', label='Knn')
plt.legend()
plt.show()

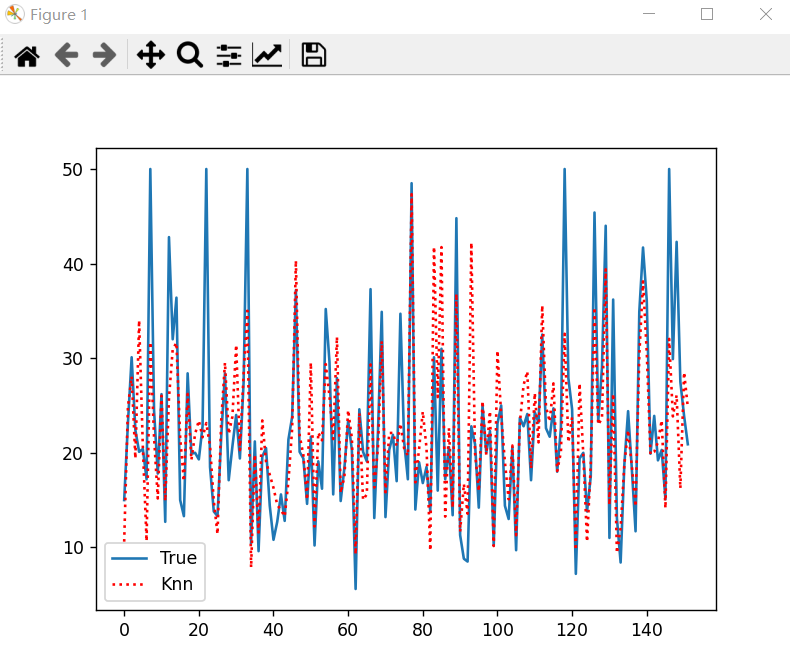
上述实现方法，预测效果较差，下面给出优化

三：回归模型预测比对

使用SelectKBest方法可以筛选出和标签最相关的K个特征，

这里选择和房价最相关的3个特征：

RM、PTRATIO、LSTAT

3-1 加载数据、获取有效信息

from sklearn.datasets import load_boston
from sklearn.neighbors import KNeighborsRegressor
from sklearn.model_selection import *
from sklearn.feature_selection import SelectKBest, f_regression  # 挑选出与标签最相关的K个特征
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import *
import numpy as np
import pandas as pd
import joblib

# 1加载数据集并获取有效信息
boston = load_boston()
print(boston.feature_names)

['CRIM' 'ZN' 'INDUS' 'CHAS' 'NOX' 'RM' 'AGE' 'DIS' 'RAD' 'TAX' 'PTRATIO'
 'B' 'LSTAT']

3-2 特征选择(3个)

# 加载数据集并获取有效信息
boston = load_boston()
# print(boston.feature_names)
# 提取特征数据
boston_data = boston['data']
# 提取标签数据
boston_target = boston['target']
# 特征选择--3个
selector = SelectKBest(f_regression, k=3)
# 3个最相关的特征
X_new = selector.fit_transform(boston_data, boston_target)
print(X_new, X_new.shape)

[[ 6.575 15.3    4.98 ]
 [ 6.421 17.8    9.14 ]
 [ 7.185 17.8    4.03 ]
 ...
 [ 6.976 21.     5.64 ]
 [ 6.794 21.     6.48 ]
 [ 6.03  21.     7.88 ]] (506, 3)

3-3 获取相关特征列的下标

# 获取相关特征列的下标
x_list = selector.get_support(indices=True).tolist()
# 和标签最相关的k个特征的下标
print(x_list)

[5, 10, 12]

如上，下标结果分别对应：RM、PTRATIO、LSTAT

3-4 数据集划分

# 数据集划分
x_train, x_test, y_train, y_test = train_test_split(X_new, boston_target, train_size=0.7, random_state=6)
print(x_train, x_train.shape)

[[ 6.567 18.4    9.28 ]
 [ 6.219 20.2   16.59 ]
 [ 7.135 17.     4.45 ]
 ...
 [ 7.163 17.4    6.36 ]
 [ 6.162 14.7    7.43 ]
 [ 5.887 20.2   16.35 ]] (354, 3)

3-5 均值方差归一化

# 均值方差归一化
standard = StandardScaler()
standard.fit(x_train)
# print(standard)
x_train_std = standard.transform(x_train)
x_test_std = standard.transform(x_test)
print(x_train_std, x_train_std.shape)

[[ 3.99220387e-01 -1.66277168e-03 -4.57295919e-01]
 [-1.01428654e-01  8.13351163e-01  6.11434949e-01]
 [ 1.21637170e+00 -6.35562499e-01 -1.16344778e+00]
 ...
 [ 1.25665380e+00 -4.54448291e-01 -8.84203461e-01]
 [-1.83431514e-01 -1.67696919e+00 -7.27768163e-01]
 [-5.79059349e-01  8.13351163e-01  5.76346658e-01]] (354, 3)

3-6 网格模型超参调优

# 选择算法、有监督学习 回归问题 
knn_model = KNeighborsRegressor()
parameter_list = [
    {
        'n_neighbors': list(range(1, 11)),
        'weights': ['distance'],
        'p': list(range(1, 6))
    },
    {
        'n_neighbors': list(range(1, 11)),
        'weights': ['uniform'],
    }
]
grid = GridSearchCV(knn_model, parameter_list, cv=7)
grid.fit(x_train_std, y_train)
print(grid.best_score_)
print(grid.best_params_)
print(grid.best_estimator_)

0.7670803829107914
{'n_neighbors': 9, 'p': 1, 'weights': 'distance'}
KNeighborsRegressor(n_neighbors=9, p=1, weights='distance')

3-7 房价预测模型

knn_reg = grid.best_estimator_
y_predict = knn_reg.predict(x_test_std)
print(y_predict)

[20.61413167 25.69014522 26.53431206 22.49276463 22.29361203 20.03067734
 12.30509611 49.31963669 23.8629333  15.66808516 25.43857778 16.71685745
 42.09414818 31.27590939 37.18674079 20.76969738 14.01746504 26.50519941
 18.99827941 13.38236798 14.60131047 29.25983529 21.40346774 23.10192473
 13.69775228 12.05762476 19.16388847 24.68013235 21.7662908  22.02178492
 23.90670944 21.36843821 26.27998708 47.54031662 15.95655019 24.16460747
 14.77397874 24.40052961 19.36083547  9.71063023  9.94329652 12.13796063
 14.58385182  8.40489325 19.66276108 23.48302845 29.40883465 22.48871882
 16.62382774 14.78819327 22.00928403 16.98691657 23.14763138 19.91953996
 38.18357785 32.31782764 16.28642224 26.66384154 14.49653769 19.93626013
 21.0910618  20.90344495 10.13254373 23.95172463 21.171378   12.42604108
 33.99524627 17.80379203 22.95047344 33.63189197 10.25926643 21.23729724
 17.06492846 17.92216224 33.06564366 25.42810344 21.50713277 47.70013793
 12.43358315 22.73541226 18.08351721 19.67990825  9.95820477 34.04765968
 20.38174808 35.46450948  9.76899009 19.70558846 12.76224312 45.96867712
  9.51119918 10.16735441 13.04497719 20.35484349 21.35950966 14.88138344
 23.80386979 17.27987054 22.45650947 11.69187726 20.9008809  24.19265661
 13.84394225 13.92241276 23.26842931  9.80813999 24.78404197 23.17245645
 27.16435427 18.84364355 24.17148621 17.11197019 27.45506657 23.26650882
 19.85980115 25.84685235 18.12905112 19.92929044 47.68624535 19.49631889
 24.15733542  8.91126671 21.86073719 21.01559513 10.37336975 17.89135825
 46.99139357 25.56999325 34.83618654 39.63717439 12.90644525 31.94668966
 11.0268659   8.17437073 19.96818107 20.83755255 20.30338769 15.91087899
 30.91401211 44.45219838 32.84033764 14.92874778 29.6394809  23.25259285
 20.14802167 16.6513891  22.97487837 27.91101101 46.15269019 13.99564029
 27.81227712 21.65462227]

3-8 利用均方根误差判断模型效果

# 利用均方根误差判断模型效果
RSME = np.sqrt(mean_squared_error(y_test, y_predict))
print(RSME)

4.59257494294638

3-9 查看数据线型图示

import matplotlib.pyplot as plt

test_pre = pd.DataFrame({"test": y_test.tolist(),
                         "pre": y_predict.flatten()
                         })
test_pre.plot(figsize=(18, 10))
plt.show()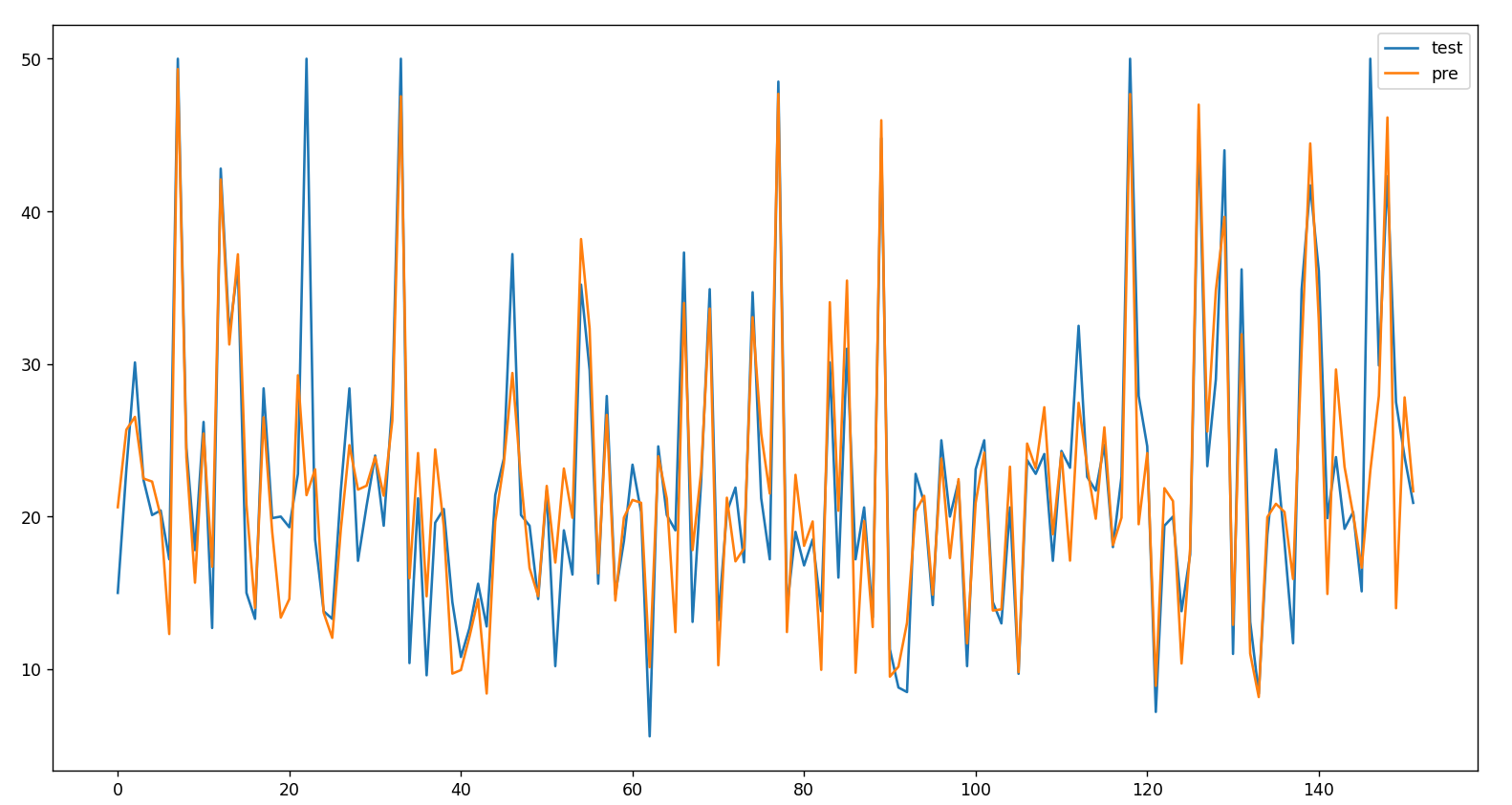

3-10 查看数据点状图示

import matplotlib.pyplot as plt

# 预测与实际
plt.scatter(y_test, y_predict, label="test")
plt.plot([y_test.min(), y_test.max()],
         [y_test.min(), y_test.max()],
         'k--',
         lw=3,
         label="predict"
         )
plt.show()

3-11 完整源码分享

from sklearn.datasets import load_boston
from sklearn.neighbors import KNeighborsRegressor
from sklearn.model_selection import *
from sklearn.feature_selection import SelectKBest, f_regression  # 挑选出与标签最相关的K个特征
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import *
import numpy as np
import pandas as pd
import joblib

# 1加载数据集并获取有效信息
boston = load_boston()
# print(boston.feature_names)
# 提取特征数据
boston_data = boston['data']
# 提取标签数据
boston_target = boston['target']
# 特征选择--3个
selector = SelectKBest(f_regression, k=3)
# 3个最相关的特征
X_new = selector.fit_transform(boston_data, boston_target)
# print(X_new, X_new.shape)
# 获取相关特征列的下标
x_list = selector.get_support(indices=True).tolist()
# 和标签最相关的k个特征的下标
# print(x_list)
# 数据集划分
x_train, x_test, y_train, y_test = train_test_split(X_new, boston_target, train_size=0.7, random_state=6)
# print(x_train, x_train.shape)
# 均值方差归一化
standard = StandardScaler()
standard.fit(x_train)
# print(standard)
x_train_std = standard.transform(x_train)
x_test_std = standard.transform(x_test)
# print(x_train_std, x_train_std.shape)

# 选择算法、有监督学习 回归问题 
knn_model = KNeighborsRegressor()
parameter_list = [
    {
        'n_neighbors': list(range(1, 11)),
        'weights': ['distance'],
        'p': list(range(1, 6))
    },
    {
        'n_neighbors': list(range(1, 11)),
        'weights': ['uniform'],
    }
]
grid = GridSearchCV(knn_model, parameter_list, cv=7)
grid.fit(x_train_std, y_train)
# print(grid.best_score_)
# print(grid.best_params_)
# print(grid.best_estimator_)

knn_reg = grid.best_estimator_
y_predict = knn_reg.predict(x_test_std)
# print(y_predict)
# 利用均方根误差判断模型效果
RSME = np.sqrt(mean_squared_error(y_test, y_predict))
# print(RSME)

import matplotlib.pyplot as plt

# 预测与实际
plt.scatter(y_test, y_predict, label="test")
plt.plot([y_test.min(), y_test.max()],
         [y_test.min(), y_test.max()],
         'k--',
         lw=3,
         label="predict"
         )
plt.show()