欢迎观看我的博客，如有问题交流，欢迎评论区留言，一定尽快回复！（大家可以去看我的专栏，是所有文章的目录）
文章字体风格：
红色文字表示：重难点✔
蓝色文字表示：思路以及想法✔
　
如果大家觉得有帮助的话，感谢大家帮忙
点赞！收藏！转发！

算法思想：

1. 二维数组的第一行表示各字符串的头结点字符
2. 每个点都有各自的idx（除了头结点）
3. cnt[N] 用于记录，以该节点结尾的点 有多少个

1. 模板

int son[N][26], cnt[N], idx;
// 0号点既是根节点，又是空节点
// son[][]存储树中每个节点的子节点
// cnt[]存储以每个节点结尾的单词数量

// 插入一个字符串
void insert(char *str)
{
    int p = 0;
    for (int i = 0; str[i]; i ++ )
    {
        int u = str[i] - 'a';
        if (!son[p][u]) son[p][u] = ++ idx;
        p = son[p][u];
    }
    cnt[p] ++ ;
}

// 查询字符串出现的次数
int query(char *str)
{
    int p = 0;
    for (int i = 0; str[i]; i ++ )
    {
        int u = str[i] - 'a';
        if (!son[p][u]) return 0;
        p = son[p][u];
    }
    return cnt[p];
}

例题-Trie字符串统计

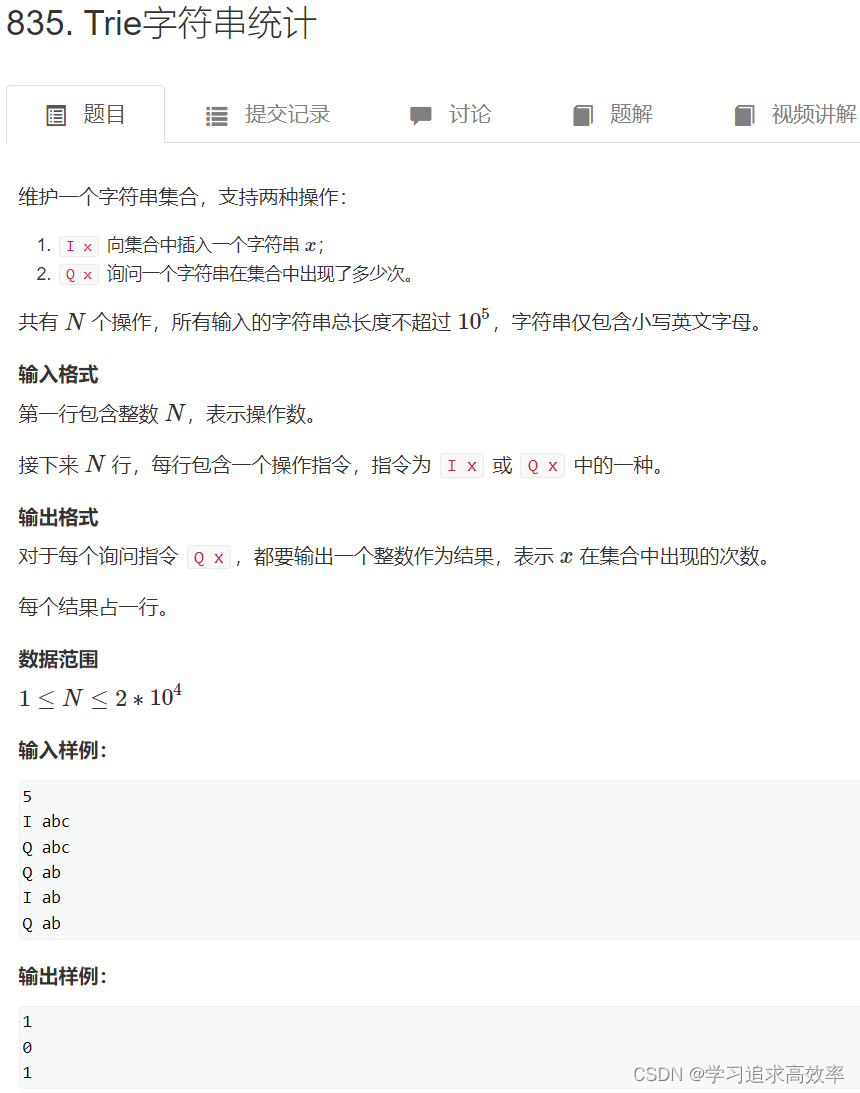
这道题主要明白 trie树的存储结构

1. son二维数组第一行 表示 各字符串的头结点
2. ab 和cb 两个字符串的b不是同一个，idx不一样
3. son存储的idx值，既是字母的地址值。也是该字母所指向的下一个字母的行数

#include<iostream>
using namespace std;

const int N = 1e6+10;
int son[N][26],idx,cnt[N];

int main()
{
    int n;
    cin >> n;
    while(n--)
    {
        char ch;
        string s;
        cin >> ch >> s;
        if(ch == 'I')
        {
            int p = 0;
            for(int i = 0; i < s.size(); i++)
            {
                if(!son[p][s[i]-'a'])
                    son[p][s[i]-'a'] = ++idx;
                p = son[p][s[i]-'a'];
            }
            cnt[p]++;
        }
        else
        {
            int p = 0,flag = 1;
            for(int i = 0; i < s.size(); i++)
            {
                if(son[p][s[i]-'a'])
                   p = son[p][s[i]-'a'];
                else
                {
                    cout << 0 << endl;
                    flag = 0;
                    break;
                }
            }
            if(flag == 1)
                cout << cnt[p] << endl;
        }
    }
    return 0;
}

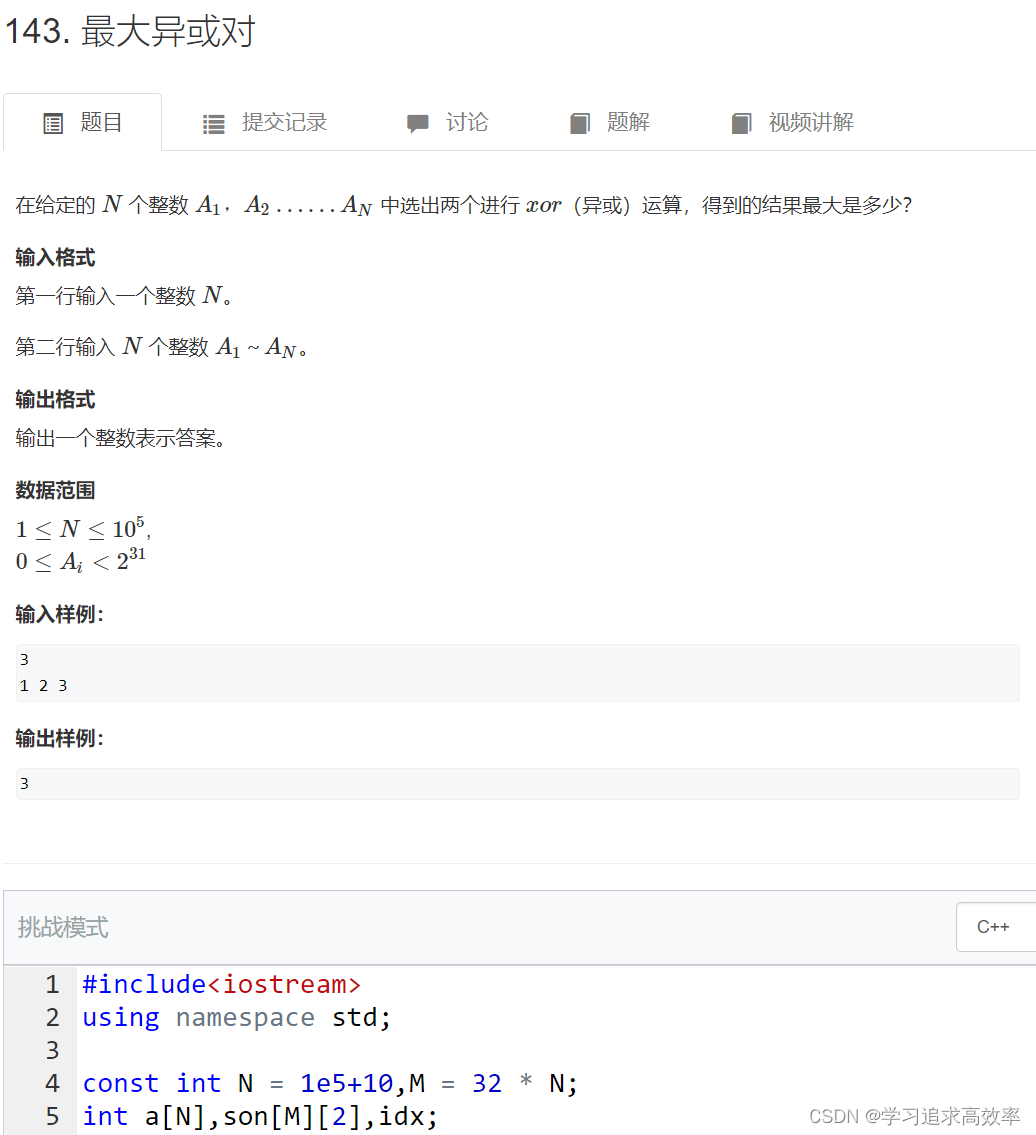
最大异或对

#include<iostream>
using namespace std;

const int N = 1e5+10,M = 32 * N;
int a[N],son[M][2],idx;

void insert(int x)
{
    int p = 0;
    for(int i = 30; i >= 0; i--)
    {
        int u = x >> i & 1;
        if(!son[p][u])
        {
            son[p][u] = ++idx;
        }
        p = son[p][u];
    }
}



int search(int x)
{
    int p = 0;
    int sum = 0;
    for(int i = 30; i >= 0; i--)
    {
        int u = x >> i & 1;
        if(son[p][!u])
        {
            sum = sum | 1 << i;
            p = son[p][!u];
        }
        else
            p = son[p][u];
    }
    return sum;
}

int main()
{
    int n;
    cin >> n;
    for(int i = 0; i < n; i++)
    {
        cin >> a[i];
        insert(a[i]);
    }
    int res = 0;
    for(int i = 0;i <n;i++)
    {
        res = max(res,search(a[i]));
    }
    cout << res;
    
    return 0;
}