青铜挑战-贪心其实很简单
1. 难以解释的贪心算法
贪心学习法则:直接做题,不考虑贪不贪心
贪心(贪婪)算法
是指在问题尽心求解时,在每一步选择中都采取最好或者最优(最有利)的选择,从而希望能够导致结果最好或者最优的算法
贪心算法所得到的结果不一定是最优的结果,但是都是相对近似最优解的结果
怎么知道什么时候改用贪心呢?
要求要解决的问题具有“最优子结构”
贪心怎么学?
将常见的贪心题都找出来看看大致是什么样子的,学一学就行了
贪心常见的应用场景?
- 排序问题:选择排序、拓扑排序
- 优先队列:堆排序
- 赫夫曼压缩编码
- 图里的 Prim、Fruska和Dijkstra算法
- 硬币找零问题
- 分数背包问题
- 并查集的按大小或者高度合并问题,或者排名
- 任务调度部分场景
- 一些复杂的近似算法
2. 贪心问题举例
2.1 分发饼干
LeetCode 455
https://leetcode.cn/problems/assign-cookies/
思路分析
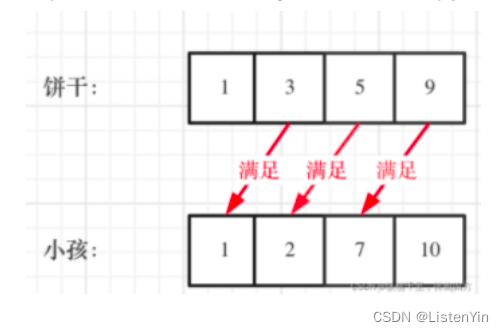
既要满足小孩的胃口,也不要造成饼干的浪费;
大饼干既可以满足胃口大的孩子,也可以满足胃口小的孩子,就应该优先满足胃口大的;
局部最优:大饼干喂给胃口大的,充分利用饼干尺寸喂饱一个
全局最优:喂饱尽可能多的孩子
贪心策略:考虑胃口,大饼干先喂饱大胃口,最后看能满足几个孩子的需要
- 先将饼干数组和小孩数组排序
- 然后从后向前比那里小孩数组,用大饼干优先满足胃口大的,并统计满足孩子的数量
代码实现
class Solution:
def findContentChildren(self, g: List[int], s: List[int]) -> int:
g.sort(reverse=True)
s.sort(reverse=True)
s_len = len(s)
s_index = 0
count = 0
for i in g:
if s_index < s_len and i <= s[s_index]:
s_index += 1
count += 1
return count
2.2 柠檬水找零
LeetCode860
https://leetcode.cn/problems/lemonade-change/
思路分析
分析下主要有三种情况
- 给的是5,直接收下
- 给的是10,给出1个5,此时必须要有1个5才行
- 给的是20,优先消耗1个10,再给1个5。如果没有10,给出3个5
局部最优:遇到账单20,优先消耗10,完成本次找零。10只能给20找零,5更万能
代码实现
class Solution:
def lemonadeChange(self, bills: List[int]) -> bool:
count_5 = 0
count_10 = 0
for money in bills:
if money == 5:
count_5 += 1
elif money == 10:
count_5 -= 1
count_10 += 1
elif money == 20:
if count_10 > 0:
count_10 -= 1
count_5 -= 1
else:
count_5 -= 3
if count_5 < 0 or count_10 < 0:
return False
return True
2.3 分发糖果
LeetCode 135
https://leetcode.cn/problems/candy/
思路分析
每个孩子至少一个糖果
相邻孩子评分更高的获得更多的糖果
- 第一轮,从左到右
- 只要右边的比左边的大,就一直加1
- 如果右边比左边小,就设置为1
- 第二轮,从右到左
- 如果左边的比右边的大,在{i+1}的基础上,先加1再赋值给{i}
- 每个位置i,从left[i]和right[i]中选最大就行了
第一轮
下标 0 1 2 3 4 5 6
得分 1 2 2 5 4 3 2
糖果 1 2 1 2 1 1 1
第二轮
下标 0 1 2 3 4 5 6
得分 1 2 2 5 4 3 2
糖果 1 2 1 4 3 2 1
选取最大
下标 0 1 2 3 4 5 6
得分 1 2 2 5 4 3 2
糖果 1 2 1 4 3 2 1
第一轮
下标 0 1 2 3 4
得分 1 3 4 5 2
糖果 1 2 3 4 1
第二轮
下标 0 1 2 3 4
得分 1 3 4 5 2
糖果 1 2 3 2 1
选取最大
下标 0 1 2 3 4
得分 1 3 4 5 2
糖果 1 2 3 4 1
代码实现
class Solution:
def candy(self, ratings: List[int]) -> int:
n = len(ratings)
candy_list = [0] * n
candy_list[0] = 1
for i in range(1, n):
if ratings[i] > ratings[i-1]:
candy_list[i] = candy_list[i-1] + 1
else:
candy_list[i] = 1
for i in range(n-2, -1, -1):
if ratings[i] > ratings[i+1]:
candy_list[i] = max(candy_list[i+1] + 1, candy_list[i])
return sum(candy_list)