前置知识

贪心算法的本质

贪心的本质是选择每一阶段的局部最优，从而达到全局最优。

例如，有一堆钞票，你可以拿走十张，如果想达到最大的金额，你要怎么拿？
指定每次拿最大的，最终结果就是拿走最大数额的钱。
每次拿最大的就是局部最优，最后拿走最大数额的钱就是推出全局最优。

什么时候用贪心算法?

感觉像是可以用贪心
用题中的案例试一下, 发现没问题
尝试举一下反例, 发现没问题
那就可以用了

所以贪心算法并没有固定的规律和套路, 也不会要求你论证背后算法的合理性和有效性, 只要能解决问题, 通过测试案例即可.

ps:个人认为贪心非常虚无缥缈呀, 还是动态规划更加有迹可循;
并且在实践过程中, 可以用贪心算法的, 基本都可以用动态规划.

什么时候不能用贪心?

当局部最优, 不一定可以达到全局最优的时候, 如:

有一堆盒子，你有一个背包体积为n，如何把背包尽可能装;
如果还每次选最大的盒子，就不行了。
这时候就需要动态规划。

贪心算法的解题步骤

将问题分解为若干个子问题
找出适合的贪心策略
求解每一个子问题的最优解
将局部最优解堆叠成全局最优解

这样的叙述非常抽象, 实践过程中还是要把握思想: 选择每一阶段的局部最优，从而达到全局最优

参考文章：关于贪心算法, 你该了解这些

455.分发饼干

题目描述

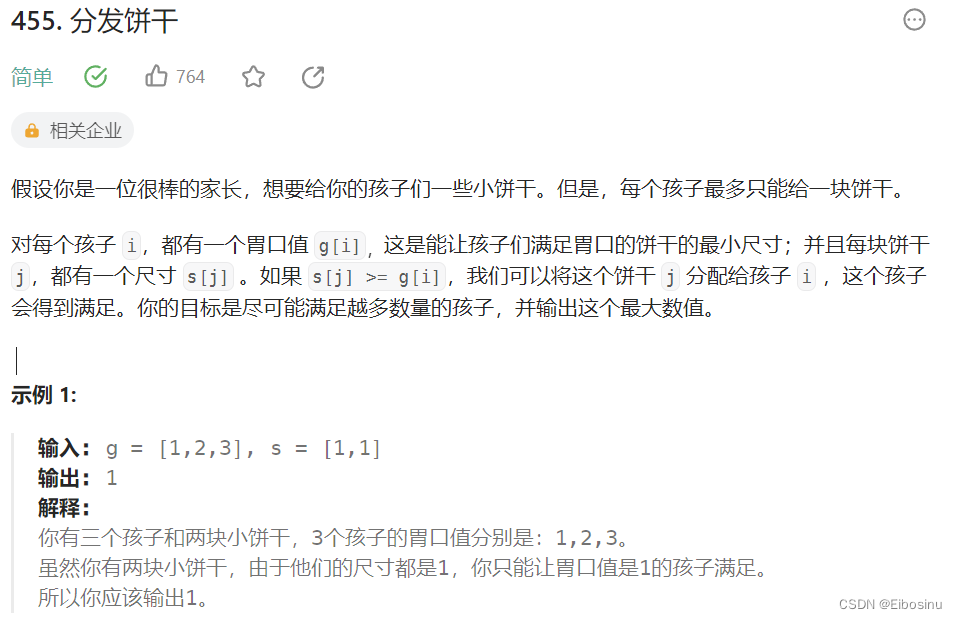
LeetCode链接：https://leetcode.cn/problems/assign-cookies/description/

解题思路

思路: 先将两个数组都srot
遍历g数组, 优先满足胃口最小的孩子
遍历g数组中的元素gg的时候, 依次遍历s数组, 选择能满足gg的最小尺寸饼干

代码

class Solution {
public:
    int findContentChildren(vector<int>& g, vector<int>& s) {
        int ans=0;
        sort(g.begin(), g.end());
        sort(s.begin(), s.end());
        int ss=0;
        for(int gg : g){
            for(; ss<s.size(); ++ss){
                if(s[ss] >= gg){
                    s[ss] = 0;
                    ans++;
                    break;
                }
            }
        }
        return ans;
    }
};

376. 摆动序列

题目描述

在这里插入图片描述

LeetCode链接：https://leetcode.cn/problems/wiggle-subsequence/description/

解题思路

<代>: 其实过程中不需要对数组进行操作, 只需要看有多少个点是符合要求的即可;
具体过程比较复杂, 建议参考其原文.

代码

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        int n=nums.size();
        if(n==0 || n==1 || (n==2 && nums[0]!=nums[1]))
            return n;
        int curDiff = 0;
        int preDiff = 0;
        int ans=1;
        for(int i=0; i<n-1; ++i){
            curDiff = nums[i+1] - nums[i];
            if((preDiff<=0 && curDiff>0) || (preDiff>=0 && curDiff<0)){
                ans++;
                preDiff = curDiff;
            }
        }
        return ans;
    }
};

53. 最大子序和

题目描述

LeetCode链接：https://leetcode.cn/problems/maximum-subarray/description/

暴力解法

思路: 暴力解法
对数组中每个数, 都依次向后遍历所有子数组, 求和, 和ans取max

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int ans=INT_MIN;
        for(int i=0; i<nums.size(); ++i){
            int sum=0;
            for(int j=i; j<nums.size(); ++j){
                sum += nums[j];
                ans = max(ans, sum);
            }
        }
        return ans;
    }
};

动态规划

不出所料的, 超出时间限制;
用动态规划, 创建数组maxSum
nums[0]的maxSum[0]就是自己本身
之后的nums[i]的maxSum[i]=max(nums[i], maxSum[i-1]+nums[i])

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        if(nums.size()==1)
            return nums[0];
        vector<int> maxSum(nums.size());
        maxSum[0] = nums[0];
        int ans=nums[0];
        for(int i=1; i<nums.size(); ++i){
            maxSum[i] = max(nums[i], maxSum[i-1]+nums[i]);
            ans = max(ans, maxSum[i]);
        }
        return ans;
    }
};

优化: 不用数组用pre

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int ans = nums[0];
        int pre = nums[0];
        for(int i=1; i<nums.size(); ++i){
            pre = max(pre+nums[i], nums[i]);
            ans = max(ans, pre);
        }
        return ans;
    }
};

贪心算法

在这里插入图片描述
选取一个个"区间", 过程中用count记录区间内的和;
当count<0时, 将其清空(=0)

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int ans = INT_MIN;
        int count=0;
        for(int i=0; i<nums.size(); ++i){
            count += nums[i];
            ans = max(ans, count);
            if(count<0)
                count = 0;
        }
        return ans;
    }
};