题目

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]

示例 2：

输入：nums = [5,7,7,8,8,10], target = 6
输出：[-1,-1]

示例 3：

输入：nums = [], target = 0
输出：[-1,-1]

提示：

• 0 <= nums.length <= 105
• -109 <= nums[i] <= 109
• nums 是一个非递减数组
• -109 <= target <= 109

算法原理

二分查找的精髓是二段性，不管数组是否有序，只要数组存在二段性（即数组可以分成两部分），那就可以使用二分查找

1 利用二分查找左端点

   假设要查找的左端点的值为t，t将整个数组分为两部分：

   区间一内的所有元素小于t   区间二内的所有元素大于等于t

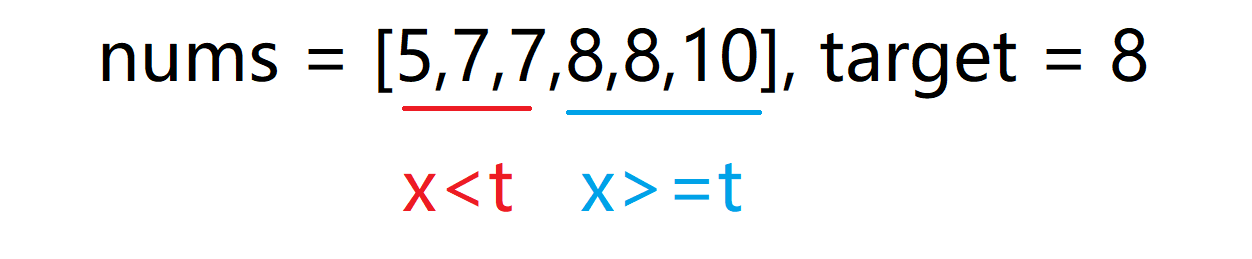
   假设每一次二分mid下标对应的值为x

   a 若是x<t  则left = mid+1

   b 若是x>=t 则right = mid  （不能是mid+1，因为mid可能就是最终答案，若是right=mid+1，那么即将检索的区间内没有了答案）

2 一些细节：

   a 循环条件：left<right

      不能是left<=right 其一是因为当left==right时已经有答案了，其二是会死循环

      

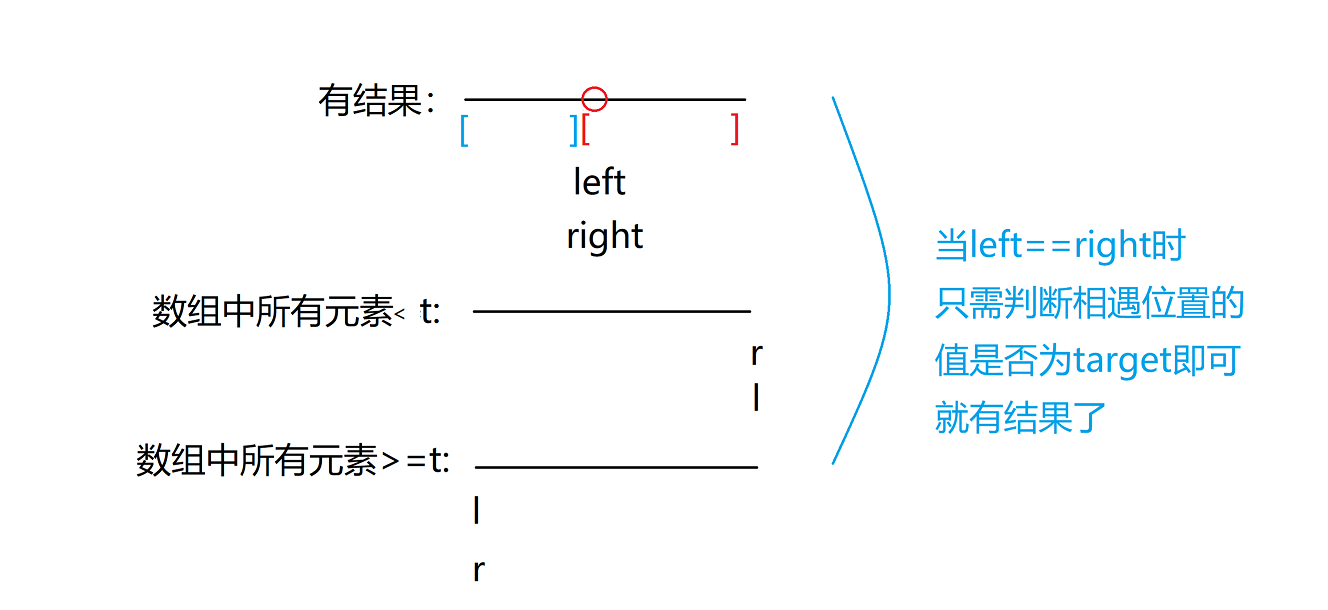
b 找中点操作：

   1 mid = left+(right-left)/2  选择这个，当区间元素数为偶数时，选择左侧的为中点

   2 mid = left+(right-left+1)/2  不选这个 当区间元素数为偶数时，选择右侧的为中点

   

查找左端点时，当区间内只剩下两个元素时 ，选择1，则mid是前一个元素，那么无论是left=mid+1，还是right=mid ，left和right最终都会相等

而选择2，mid是后一个元素，若是执行right=mid，那么陷入死循环

3 利用二分查找右端点 

   a 若是x<=t 则left = mid（不能是mid+1，因为mid可能是最终结果）

   b 若是x>t 则right = mid-1

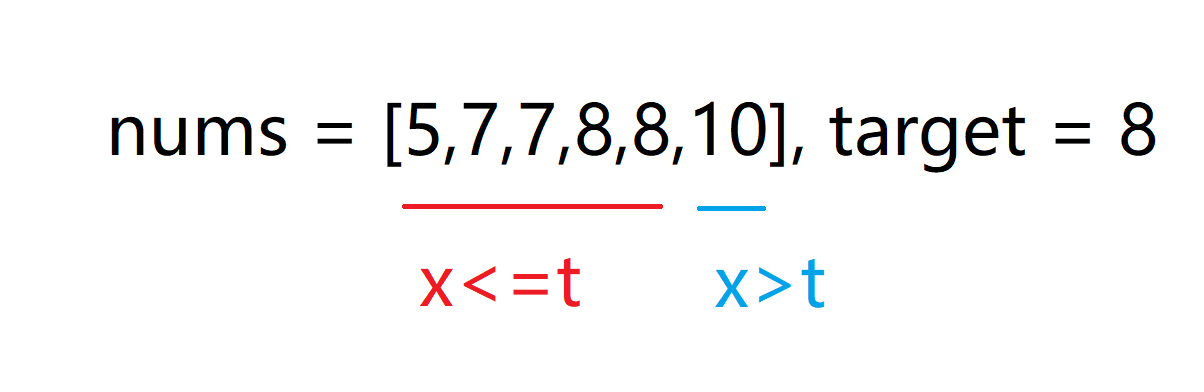
c 循环条件：left<right

   求中点：mid = left+(right-left+1)/2  left最终都会等于right 

                 若是选择 mid = left+(right-left)/2，当执行left=mid时，陷入死循环

代码实现：

class Solution 
{
public:
    vector<int> searchRange(vector<int>& nums, int target) 
    {
        if(nums.empty())//处理边界情况
        {
            return {-1,-1};
        }
        //1 二分找左端点
        int left = 0;
        int right = nums.size()-1;
        while(left<right)
        {
            int mid = left+(right-left)/2;
            if(nums[mid]<target)
            {
                left = mid+1;
            }
            else 
            {
                right = mid;
            }
        }

        int begin = 0;
        if(nums[left]==target)
        {
            begin = left;
        }
        else 
        {
            return {-1,-1};
        }

        //2 二分找右端点
        left = 0;
        right = nums.size()-1;
        while(left<right)
        {
            int mid = left+(right-left+1)/2;
            if(nums[mid]<=target)
            {
                left = mid;
            }
            else 
            {
                right = mid-1;
            }
        }
        return {begin,left};
    }
};