226 翻转二叉树 easy

这道题有一段广为人知的传说：曾有人说Homebrew（适用于macOS和Linux的开源软件包管理器）的作者Max Howell，没有在白板上写出这道题目，被Google拒绝了。

至于是不是真的因为没做出来这道题就被拒绝，我想只有面试官自己本人清楚了。

回到正题，翻转二叉树的意思，就是将一棵数的左右子树完全交换

什么叫做完全交换呢？参考下图，不仅2与7发生了交换，且7的左右子树6和9也发生了交换。

此前我们讲完了二叉树的深度遍历和层序遍历。也是从这道题开始，之后的题目，大多情况下我们都需要想一想应该用那种遍历方式。

那么这道题应该用哪种呢？

我首先想到的是层序遍历，将每一层每两个节点做一次交换就可以。

或者也可以用前序遍历或者后序遍历，因为在这两种遍历中，左右节点是依次处理的。中序遍历却不可以。

所以这道题，可以用深度优先的递归法和迭代法 +广度优先遍历的迭代法，三种方法来解决，颇有种三英战吕布（easy level）的意味。

深度优先，递归法——

void reverse(TreeNode* cur) {
    if (!cur) return;
    swap(cur->left, cur->right);
    reverse(cur->left);
    reverse(cur->right);
}
TreeNode* invertTree(TreeNode* root) {
    if (!root) return root;
    reverse(root);
    return root;
}

还有一种更加简洁的写法，直接调用本函数完成递归，代码如下：

TreeNode* invertTree(TreeNode* root) {
    if (!root) return root;
    swap(root->left, root->right);
    invertTree(root->left);
    invertTree(root->right);
    return root;
}

深度优先，迭代法——

刚刚提到使用前序或者后序遍历都可以，此处我们就使用前序遍历来完成，代码如下：

TreeNode* invertTree(TreeNode* root) {
    stack<TreeNode*> stk;
    if (root) stk.push(root);
    while (!stk.empty()) {
        TreeNode *cur = stk.top();
        stk.pop();
        swap(cur->left, cur->right);
        if (cur->left) stk.push(cur->left);
        if (cur->right) stk.push(cur->right);
    }
    return root;
}

此前我们也跟着随想录，走了一遍如何使用统一写法（基于标记法），完成三种遍历，所以此处也附上使用统一写法的前序遍历，代码如下——

TreeNode* invertTree(TreeNode* root) {
    stack<TreeNode*> stk;
    if (root) stk.push(root);
    while (!stk.empty()) {
        TreeNode *cur = stk.top();
        // 统一写法中最关键的地方
        if (cur) {
            stk.pop();
            if (cur->right) stk.push(cur->right);
            if (cur->left) stk.push(cur->left);
            stk.push(cur);
            stk.push(nullptr);
        } else {
            stk.pop();
            cur = stk.top();
            stk.pop();
            swap(cur->left, cur->right);
        }
    }
    return root;
}

最后一种方法，就是广度优先遍历，即层序遍历，代码如下：

TreeNode* invertTree(TreeNode* root) {
    queue<TreeNode*> que;
    if (root != NULL) que.push(root);
    while (!que.empty()) {
        int size = que.size();
        for (int i = 0; i < size; i++) {
            TreeNode* node = que.front();
            que.pop();
            swap(node->left, node->right); // 节点处理
            if (node->left) que.push(node->left);
            if (node->right) que.push(node->right);
        }
    }
    return root;
}

101 对称二叉树 easy

这道题教会了我们对称二叉树的定义，见下图即可：

首先判断应该用那种遍历方式。对称，从感觉上讲层序遍历可以解决问题，但对每一层的值进行判断，会相当耗费时间。

那么这道题可以从深度遍历的角度考虑，前中后序应该用哪一种又成了问题。

其实这道题只能用“后序”遍历，因为对于这道题而言，是否为对称，要先看左右子树是否符合条件，根节点的优先级在最后。为什么要给后序加一个引号呢？是因为这道题已经并非是正统的后序遍历了。我们要对左右子树进行判断，那么比较的对象就是：

左结点的左孩子与右结点的右孩子，左节点的右孩子和右结点的左孩子，顺序是相反的。

这道题可以使用递归，迭代来完成。

递归法要通过返回比较结果，所以返回值是bool类型；那么结束条件就分四种：

{左右都为空，返回true}，{左右其中一个不存在，返回false}，{左右值都存在，但是却不相同，返回false}，那么最终剩下的结果，就是左右都存在且值相同。

递归法的代码（简洁版）如下：

bool compare(TreeNode* left, TreeNode* right) {
    if (left == NULL && right != NULL) return false;
    else if (left != NULL && right == NULL) return false;
    else if (left == NULL && right == NULL) return true;
    else if (left->val != right->val) return false;
    else return compare(left->left, right->right) && compare(left->right, right->left);
}

bool isSymmetric(TreeNode* root) {
    if (root == NULL) return true;
    return compare(root->left, root->right);
}

那么使用迭代法呢？刚刚我们说过了这道题并非正统的后序遍历，所以遍历顺序自然要符合题意。迭代法我们首先会想到使用栈，但这道题因为每两个节点就要比较一次，所以使用队列也是可以的，在代码中用哪种都可以，此处我们使用队列，代码如下：

bool isSymmetric(TreeNode* root) {
    if (!root) return true;
    queue<TreeNode*> que;   
    que.push(root->left);
    que.push(root->right);
    while (!que.empty()) {
        TreeNode *leftNode = que.front();
        que.pop();
        TreeNode *rightNode = que.front();
        que.pop();
        if (!leftNode && !rightNode) continue;
        if (!leftNode || !rightNode || (leftNode->val != rightNode->val))
            return false;
        // 注意入队顺序
        que.push(leftNode->left);
        que.push(rightNode->right);
        que.push(leftNode->right);
        que.push(rightNode->left);
    }
    return true;
}

接下来提到的这两道题，属于对称二叉树的变种，稍微修改一下就可以AC，所以也就不再深入的理解了。

100 相同的树 easy

检测两棵数是否相同，方法从比较一棵树，变成了真的比较“左右两棵子树”

递归法代码如下：

bool compare(TreeNode *cur1, TreeNode *cur2) {
    if (cur1 == nullptr && cur2 == nullptr) return true;
    else if (cur1 != nullptr && cur2 == nullptr) return false;
    else if (cur1 == nullptr && cur2 != nullptr) return false;
    else if (cur1->val != cur2->val) return false;
    else return compare(cur1->left, cur2->left) && compare(cur1->right, cur2->right);
}

bool isSameTree(TreeNode* p, TreeNode* q) {
    return compare(p, q);
}

572 另一个树的子树 easy

判断一棵树中是否包含另一棵树，见下图：

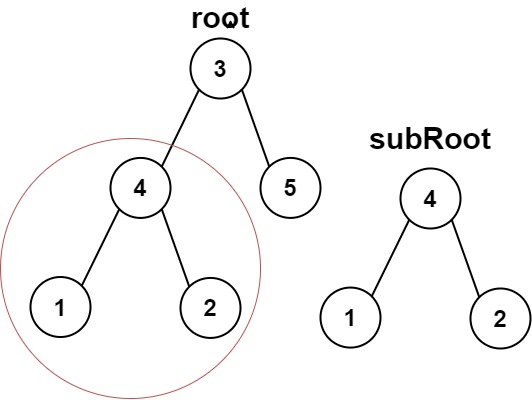
同样使用迭代法，代码如下：

bool compare(TreeNode* left, TreeNode* right) { 
    if (left == nullptr && right != nullptr) return false;
    else if (left != nullptr && right == nullptr) return false;
    else if (left == nullptr && right == nullptr) return true;
    else if (left->val != right->val) return false;

    return compare(left->left, right->left) && compare(left->right, right->right);
}

bool isSubtree(TreeNode* root, TreeNode* subRoot) {
    if (root == nullptr) return false;

    return compare(root, subRoot) || isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
}