题目：

给定数组arr，arr中所有的值都为正数且不重复。每个值代表一种面值的货币，每种面值的货币可以使用任意张，在给定一个整数aim，代表要找的钱数，求组成aim的最少货币数。

示例：

arr = [5,2,3] , ami=20

4张5元的可以组成20，其他方案需要更多张货币，所以返回4。

arr = [3,5] ，aim=2

无法组成2，返回 -1

方法一：暴力递归

每一种面值都尝试不同的张数

对于 arr = [5,2,3]从0开始，就是

先用0张5元的，剩下20由面值2，3处理，

再用1张五元的，剩下15由面值2，3处理，

再用2张五元的，剩下10由面值2，3处理，

再用3张五元的，剩下5由面值2，3处理，

再用4张五元的，剩下0由面值2，3处理。

对于面值2，3 用同样的方式处理。

代码实现：

    public static int minCoinsl(int[] arr, int aim) {
        if (arr == null || arr.length == 0 || aim < 0) {
            return -1;
        }
        return process(arr,0,aim);
    }

    //arr=[5,2,3] aim=20, 4张五元
    //当前考虑的面值为arr[i] 还剩rest的钱需要找零
    public static int process(int[] arr, int i, int rest) {
        //i=arr.length的时候，数组中的面值都已经用过
        //如果当时剩余的钱rest是0，就返回0张
        //如果当时剩余的钱不是0，就返回-1
        if (i == arr.length) {
            return rest == 0 ? 0 : -1;
        }
        //初始化需要的货币数 num=-1
        int num = -1;
        //对于当前的面值，依次从0张，1张，2张..往下遍历，终止条件就是 张数*面值<=剩余钱数
        for (int k = 0; k * arr[i] <= rest; k++) {
            //使用了k张当前面值，剩余钱rest=rest-k*当前面值
            //然后剩余的钱交给后面的面值来处理
            int next = process(arr, i+1, rest-k*arr[i]);
            //如果剩下的钱经过后面的面值没有处理完，就返回 -1
            //next != -1 说明剩下的钱可以由后面的面值来处理
            if (next != -1) {
                //如果当前货币数为-1，就将货币数设置为 next+k，否则就设置为 当前货币数和next+k中更小的那个
                num = num == -1 ? next + k : Math.min(num, next+k);
            }
        }
        return num;
    }

方法二：暴力递归改动态规划

注意在代码中初始化的 dp 是N+1行 aim+1 列

因为会考虑到 i==arr.length时的这一行。rest属于[0，aim]，本身就是aim+1列

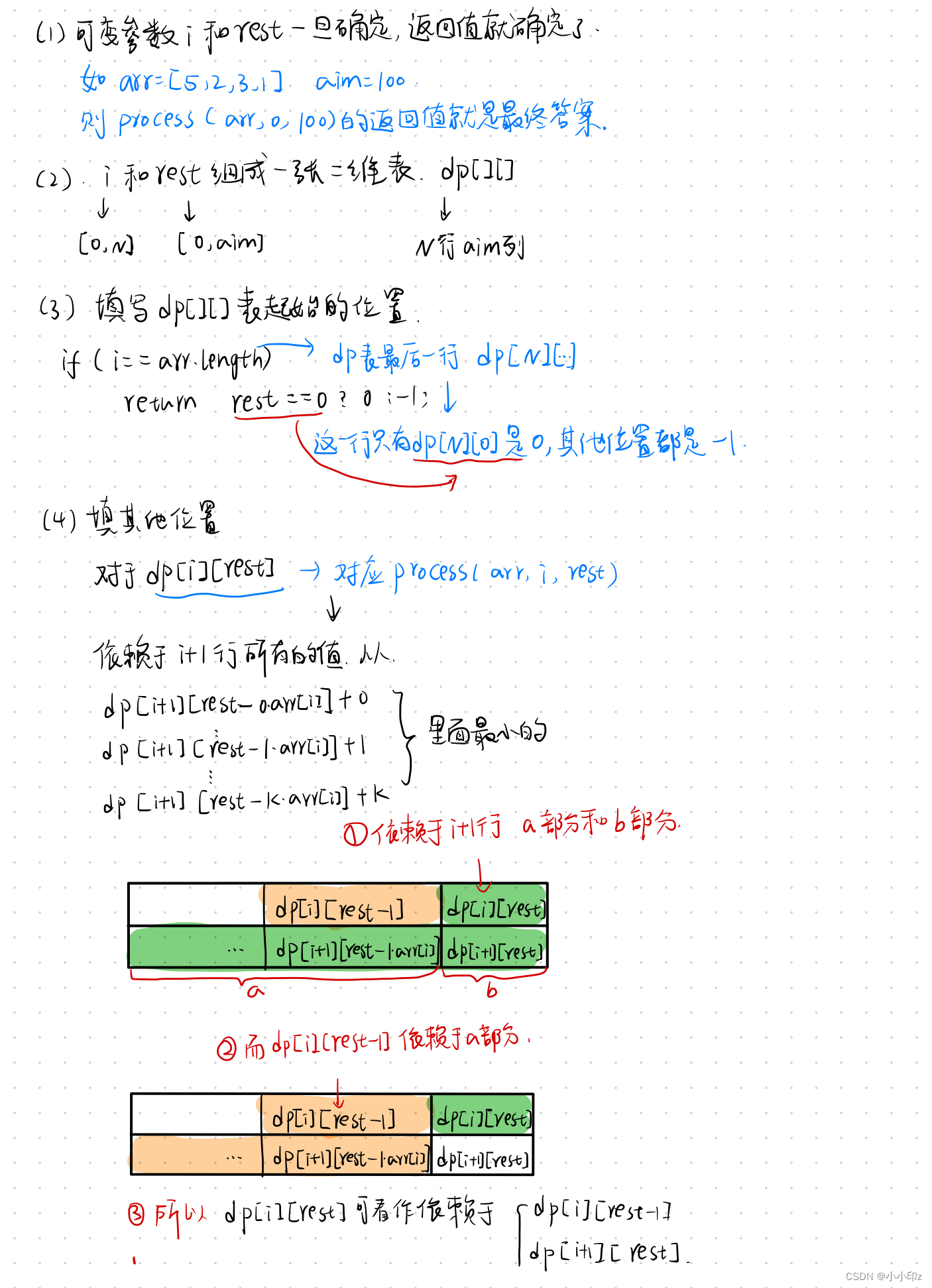
 代码实现：

    public static int minCoins2(int[] arr, int aim) {
        if (arr == null || arr.length == 0 || aim < 0) {
            return -1;
        }
        int N = arr.length;
        int[][] dp = new int[N+1][aim+1];
        //设置最后一排的值，除dp[N][0]为0外，其他都是-1
        for (int col = 1; col <=aim; col++) {
            dp[N][col] = -1;
        }
        for (int i = N-1; i >= 0; i--) {//从下往上计算每一行
            for (int rest = 0; rest <= aim; rest++) {
                dp[i][rest] = -1;//开始时先设置 dp[i][rest]为无效
                if (dp[i+1][rest] != -1) {
                    dp[i][rest] = dp[i+1][rest];//先设置成下面的值
                }
                //然后看他依赖的左边位置是否越界且有效  如果不越界并且有效
                if (rest - arr[i] >=0 && dp[i][rest-arr[i]] != -1) {
                    //再判断 当前dp[i][rest] == -1是否成立，如果成立，说明dp[i+1][rest]也是-1
                    //那么直接将左边的值赋值给dp[i][rest]
                    if (dp[i][rest] == -1) {
                        dp[i][rest] = dp[i][rest-arr[i]] + 1;
                    } else {
                        //当前dp[i][rest] == -1是否成立，如果不成立，那就比较当前dp[i][rest]和他左边谁小，谁小用谁
                        dp[i][rest] = Math.min(dp[i][rest],dp[i][rest-arr[i]] + 1);
                    }
                }
            }
        }
        return dp[0][aim];
    }