题目精选

6-7 统计某类完全平方数

我们先看一下题目要求：
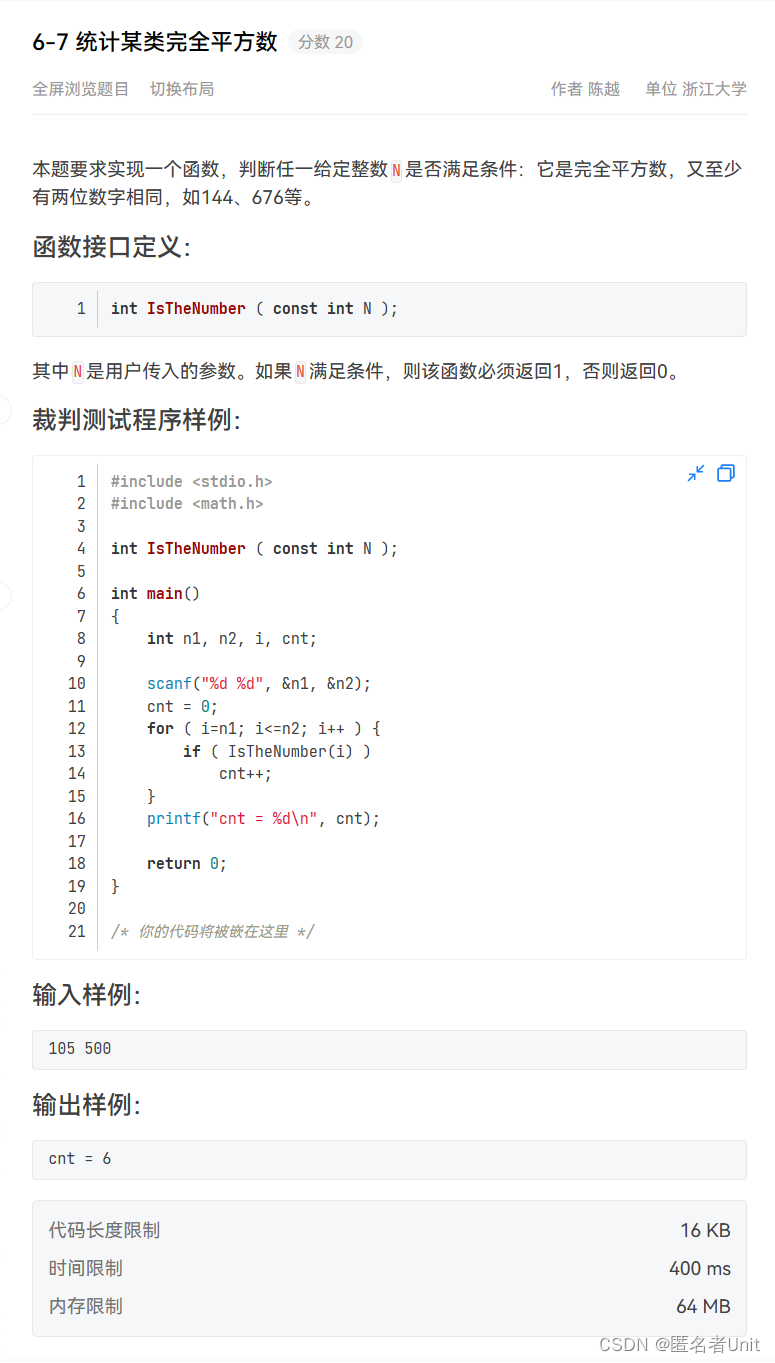
在这里插入图片描述
根据题目给出的要求：完全平方数、至少有两位相同的数，我们可以将非完全平方数排除在外：

int IsTheNumber(const int N)
{
	if (（N <= 0）||（sqrt(N) - (int)sqrt(N) > 0）)
    	{
      	  return 0;
   		}
}

这里我使用了sqrt来判断完全平方数，根据MSDN

double sqrt( double x );

我们可知sqrt返回double类型的数值，通过强制类型转换int再作差可将非完全平方数筛查出来。
那么相同数字的个数又如何判断呢？这里我们想到可以通过while循环将N的每一位拿下来，通过一个大小为十的数组和计数器进行判断。
完整代码附上，大家仔细体会：

int IsTheNumber(const int N)

{
    if (（N <= 0）||（sqrt(N) - (int)sqrt(N) > 0）)
    {
        return 0;
    }
    else
    {
        int M = N;//形参是const修饰的常变量
        int ch[10] = { 0 };
        while (M > 0)
        {
            for (int i = 0; i <= 9; i++)
            {
                if (M % 10 == i)
                {
                    ch[i] += 1;
                    if (ch[i] == 2)
                    {
                        return 1;
                    }
                }

            }
            M = M / 10;
        }
        return 0;
    }
}

6-9 统计个位数字

我们先来看一下题目：
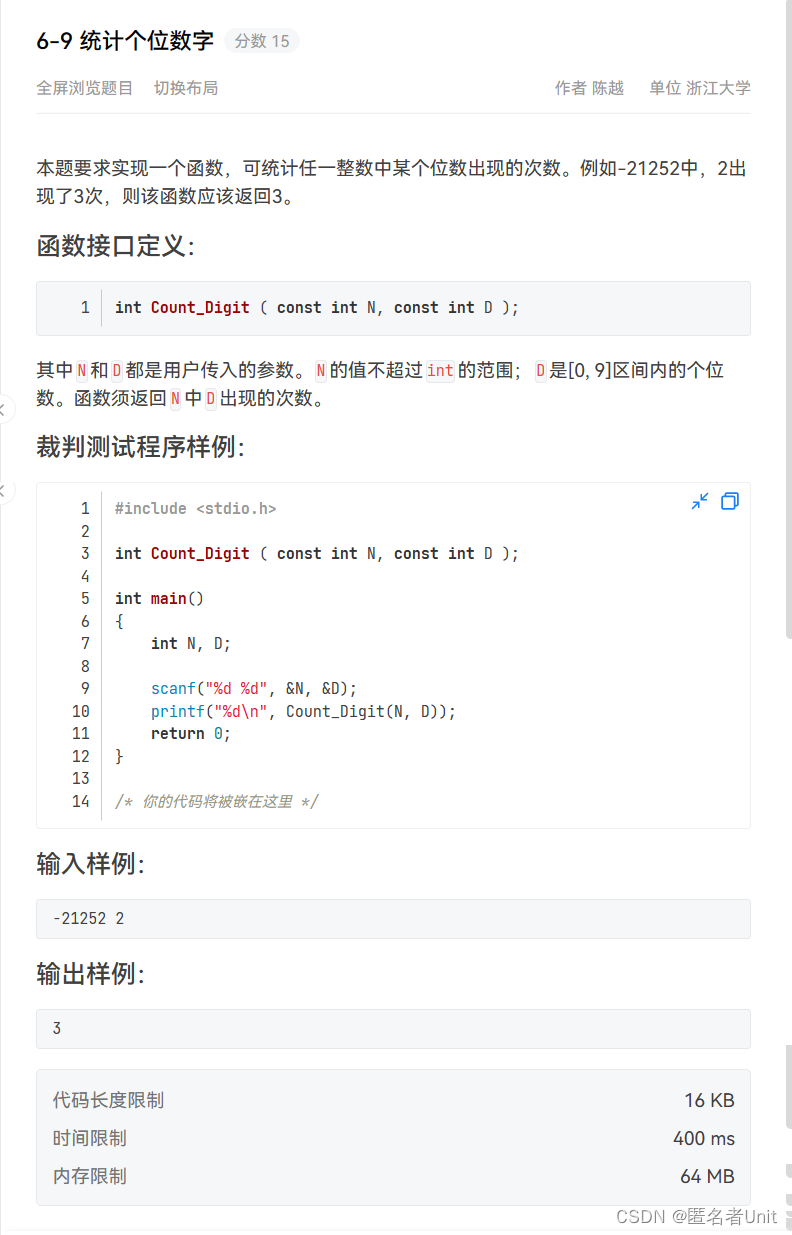
在这里插入图片描述
这题比较简单使用while判断每一位，再注意下题目的细节即可AC

int Count_Digit ( const int N, const int D )
{
    int count=0;
    if(N<0)
    {
        int a=-N;
        while(a>0)
        {
            if(a%10==D)
            {
                count++;
            }
            a=a/10;
        }
        return count;
    }
    else if(N==0)
        return 1;
    else
    {
        int a=N;
        
        while(a>0)
        {
            if(a%10==D)
            {
                count++;
            }
            a=a/10;
        }
        return count;
    }
}

6-10 阶乘计算升级版

题目：
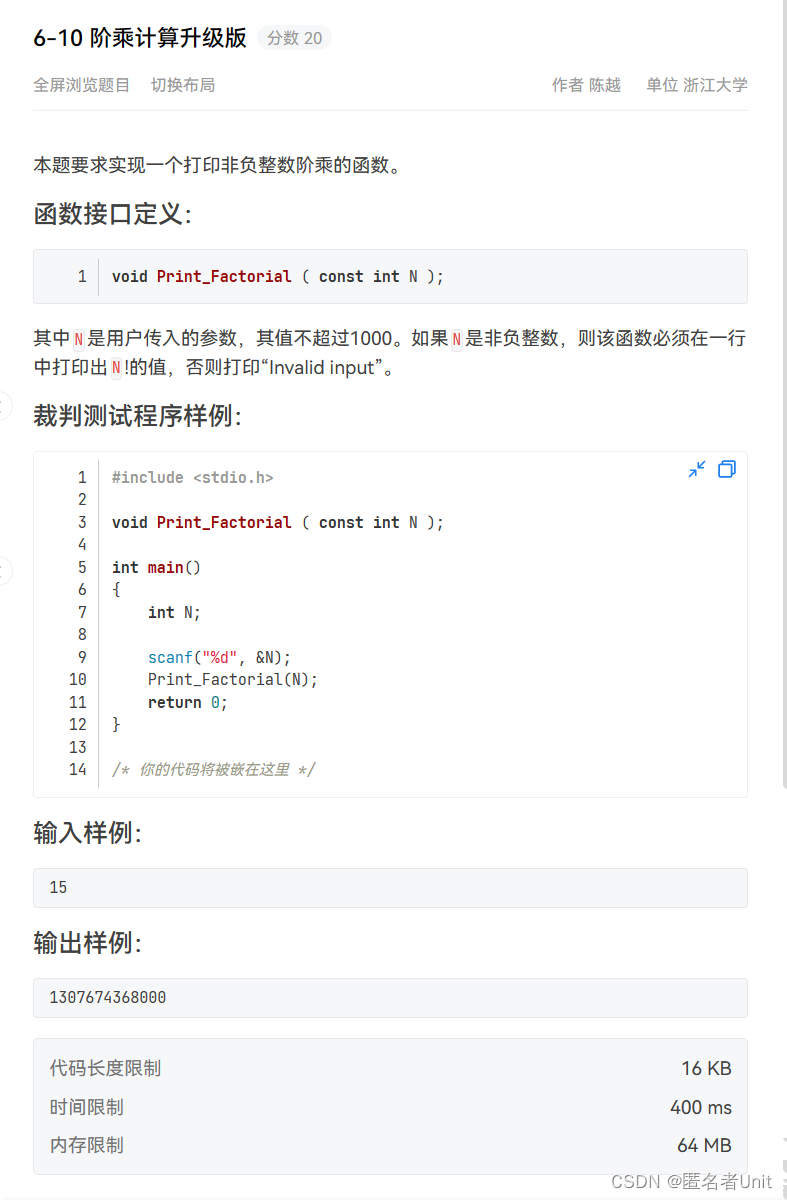
在这里插入图片描述
乍一看这题不就是求个阶乘吗？我就讲代码放上去：

void Print_Factorial ( const int N )
{
    if(N<0)
        printf("Invalid input");
    else
    {
        long long num=1;
        for(int i=1;i<=N;i++)
        {
            num*=i;
        }
        printf("%ld",num);
    }
}

结果发现当N取得比较大是，阶乘数就远超出了long long的数据范围。
这里我们就要了解一个新的算法思想————高精度算法，当我们遇到连最大范围的longlong都无法储存的情况下，需要通过特殊的方法计算出我们想要的答案。
那我们就通过此题初窥高精度算法。

转载：
原文链接
例如4的阶乘为24，则num[0]=4，num[1]=2
这种方法的原理就是将数字的每一位拆分出来存到数组，在求阶乘时，每一次乘法都分解为数组的每一位乘这个数，例如：
2的阶乘，num[0]=num[0]*2%10=2；
3的阶乘，num[0]=num[0]*3%10=6；
4的阶乘，num[0]=num[0]*4%10=4，而此时产生了进位，进位为2，所以num[1]=进位=2；
而5的阶乘，num[0]=num[0]*5%10=0，进位为2，num[1]=(num[1]*5+进位)%10=2，进位为1，num[2]=进位=1；得到5的阶乘为120。

代码如下：

void Print_Factorial(const int N) {
    if (N < 0)
        printf("Invalid input");
    else {
        int num[3000] = { 0 }, j, n = N;    //num记录各个位上的数字，全初始化为0
        num[0] = 1;                   //个位初始化为1
        int l = 0;                    //记录结果的位数
        int carry = 0;                //低位向高位的进位
        for (int i = 2; i <= n; i++) {
            for (j = 0; j <= l; j++) {
                int temp = num[j] * i + carry;
                num[j] = temp % 10;     //该位的数
                carry = temp / 10;      //进位的数
            }
            while (carry) {          //拓展结果的总位数记录进位的数，直到进位为0
                num[j++] = carry % 10;  //该位的数
                carry /= 10;          //进位的数
                l++;
            }
        }
        for (; l >= 0; l--)              //数组按照从地位到高位的方式存储结果，逆向输出结果
            printf("%d", num[l]);
    }
}

6-11 求自定类型元素序列的中位数

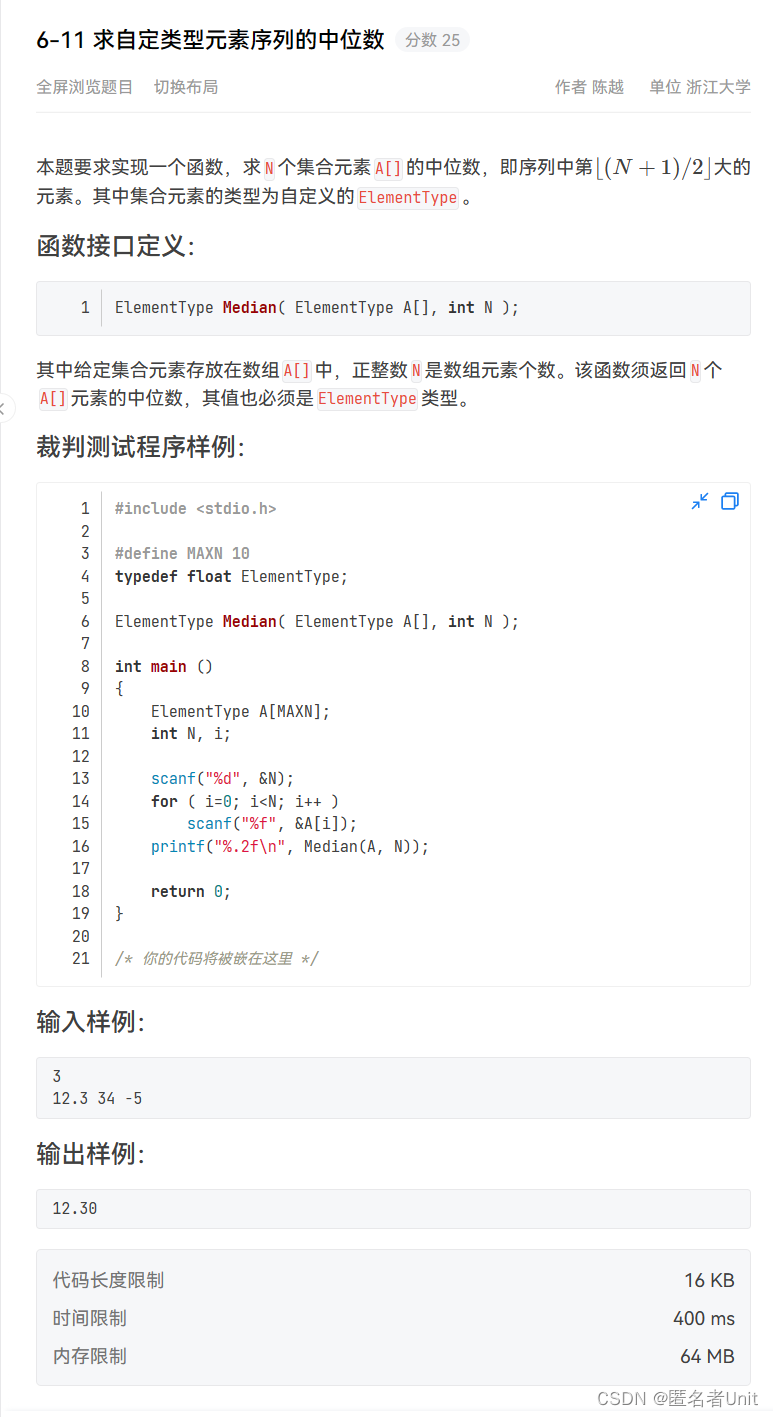
在这里插入图片描述
这题的思路就很清晰，先将传过来的数组排序，再返回中位数即可。有两点需要注意的当N为偶数时，中位数并不是中间两个数的平均数，而是较大的那个，这是题目与我们常识不同的地方。还有就是，排序方法的选择，如果你使用冒泡排序的话，会有一个测试点卡时，导致无法AC。而我使用了快排qsort函数，代码如下奉上，其实下面的代码还是有不足的地方，你能发现吗？评论或者私信教教我吧。

int cmp(const void* a, const void* b) //当然，可以直接写为int cmp ( const int\* a , const int\* b ) 
{
    return *(ElementType*)a - *(ElementType*)b;//回调函数
}


ElementType Median(ElementType A[], int N)
{
    qsort(A, N, sizeof(ElementType), cmp);//快排qsort 头文件<stdlib.h>
   /* for (int i = 0; i < N - 1; i++)
    {
        int j = 0;
        for (j = 0; j < N - i - 1; j++)
        {
            if (A[j] > A[j + 1])
            {
                ElementType tmp = A[j];
                A[j] = A[j + 1];
                A[j + 1] = tmp;
            }
        }
    }*/
    if (N % 2 == 0)
    {
        //ElementType sum = (A[N / 2 - 1] + A[(N + 2) / 2 - 1]) / 2;
        return (A[N / 2 - 1] > A[(N + 2) / 2 - 1] ? A[N / 2 - 1] : A[(N + 2) / 2 - 1]);
    }
    else
        return A[(N + 1) / 2 - 1];
}