简单DP+最长上升子序列

文章目录

简单DP+最长上升子序列
比较简单的DP
- [1027. 方格取数](https://www.acwing.com/problem/content/1029/)
- - 题解
- [275. 传纸条](https://www.acwing.com/problem/content/277/)
- - 题解
最长上升子序列
- [AcWing1014. 登山](https://www.acwing.com/problem/content/1016/)
- - 题解
- [AcWing1012. 友好城市](https://www.acwing.com/problem/content/1014/)
- - - 输入格式
    - 输出格式
    - 数据范围
    - 输入样例：
    - 输出样例：
  - 代码
- [1010. 拦截导弹](https://www.acwing.com/problem/content/description/1012/)
- [187. 导弹防御系统](https://www.acwing.com/problem/content/description/189/)
- - - 样例解释
  - 题解（DFS）
  - - DFS+剪枝
  - 题解（迭代加深）
- [272. 最长公共上升子序列](https://www.acwing.com/problem/content/description/274/)
- - - 输入格式
    - 输出格式
    - 数据范围
    - 输入样例：
    - 输出样例：
  - 题解
  - 最终代码

比较简单的DP

1027. 方格取数

设有 N×N 的方格图，我们在其中的某些方格中填入正整数，而其它的方格中则放入数字0。如下图所示：

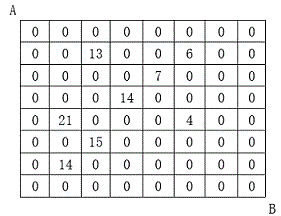
某人从图中的左上角 A 出发，可以向下行走，也可以向右行走，直到到达右下角的 B 点。

在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字0）。

此人从 A 点到 B 点共走了两次，试找出两条这样的路径，使得取得的数字和为最大。

输入格式

第一行为一个整数N，表示 N×N 的方格图。

接下来的每行有三个整数，第一个为行号数，第二个为列号数，第三个为在该行、该列上所放的数。

行和列编号从 1开始。

一行“0 0 0”表示结束。

输出格式

输出一个整数，表示两条路径上取得的最大的和。

数据范围

N≤10≤10

输入样例：

输出样例：

题解

不可以使用贪心（第一次选择最大的一条路径，然后把已经选择过的清空，再选择）

反例：

0  1  0
2  2  2
1  0  0

这里使用f[x1][y1][x2][y2]来进行描述。

但是发现存在状态冗余，所以取一个为横纵坐标之和

#include <bits/stdc++.h>
using namespace std;
#define N 15
int a[N][N];
int dp[N * 2][N][N];
int n;
int dx[4] = {0, 0, -1, -1};
int dy[4] = {-1, 0, -1, 0};
int solve()
{
    for(int k = 2;  k <= n * 2; k++)
    {
        for(int i = 1; i < k && i <= n; i++)
        {
            for(int j = 1; j < k && j <= n; j++)
            {
                int maxv = 0;
                for(int p = 0; p < 4; p++)
                {
                    int ni = i + dx[p];
                    int nj = j + dy[p];
                    maxv = max(maxv, dp[k - 1][ni][nj]);
                }
                if(i == j) dp[k][i][j] = maxv + a[i][k - i];
                else dp[k][i][j] = maxv + a[i][k - i] + a[j][k - j];
            }
        }
    }
    return dp[n * 2][n][n];
}
int main()
{
    scanf("%d", &n);
    int x, y, z;
    while(scanf("%d%d%d", &x, &y, &z), x || y || z)
    {
        a[x][y] = z;
    }
    cout << solve() << endl;
    return 0;
}

小渊和小轩是好朋友也是同班同学，他们在一起总有谈不完的话题
一次素质拓展活动中，班上同学安排坐成一个 m行n列的阵，而小渊和小轩被安排在知阵对角线的两端，因此，他们就无法直接交谈了
幸运的是，他们可以通过传纸条来进行交流
纸条要经由许多同学传到对方手里，小渊坐在矩阵的左上角，坐标(1,1)，小轩坐在矩阵的右下角，坐标(m,n)。
从小渊传到小轩的纸条只可以向下或者向右传递，从小轩传给小渊的纸条只可以向上或者向左传递。
在活动进行中，小渊希望给小轩传递一张纸条，同时希望小轩给他回复
班里每个同学都可以帮他们传递，但只会帮他们一次，也就是说如果此人在小渊递给小轩纸条的时候帮忙，那么在小轩递给小渊的时候就不会再帮忙，反之亦然。
还有一件事情需要注意，全班每个同学愿意帮忙的好感度有高有低注意:小渊和小轩的好心程度没有定义，输入时用0表示)，可以用一个0~100的自然数来表示，数越大表示越好心。
小渊和小轩希望尽可能找好心程度高的同学来帮忙传纸条，即找到来回两条传递路径，使得这两条路径上同学的好心程度之和最大。
现在，请你帮助小渊和小轩找到这样的两条路径

输入格式
第一行有2个用空格隔开的整数m和n，表示学生矩阵有m行n列接下来的m行是一个mxn的阵，知阵中第行列的整数表示坐在第行列的学生的好心程度，每行的n个整数之间用空格隔开。
输出格式
输出一个整数，表示来回两条路上参与传递纸条的学生的好心程度之和的最大值.
数据范围
1<=n,m <=50

输入样例：

输出样例：

题解

这一道题目可以直接使用上面的代码。

使用上面的代码求解出来的路径：

如果两条路径并没有相交，那么就是这一道题目的结果
如果方块取数的路径有相交的，那么我可以把相交处往外折叠，这样，折叠之后的结果一定优于或与未折叠的一样。而由于方块取数求的是最优解。所以折叠之后的结果等于未折叠的解
而折叠之后的解就是这一道题目的解。

我就算考虑可以相交的情况，最优解也不过如此，所以上述方法求出来的就是最优解。

使用上一道题目的代码

#include <bits/stdc++.h>
#include <cstdio>
using namespace std;
#define N 55
int a[N][N];
int dp[N * 2][N][N];
int n, m;
int dx[4] = {0, 0, -1, -1};
int dy[4] = {-1, 0, -1, 0};
int solve()
{
    for(int k = 2;  k <= n + m; k++)
    {
        for(int i = 1; i < k && i <= n; i++)
        {
            for(int j = 1; j < k && j <= n; j++)
            {
                int maxv = 0;
                for(int p = 0; p < 4; p++)
                {
                    int ni = i + dx[p];
                    int nj = j + dy[p];
                    maxv = max(maxv, dp[k - 1][ni][nj]);
                }
                if(i == j) dp[k][i][j] = maxv + a[i][k - i];
                else dp[k][i][j] = maxv + a[i][k - i] + a[j][k - j];
            }
        }
    }
    return dp[n+m][n][n];
}
int main()
{
    scanf("%d%d", &n, &m);
   for(int i = 1; i <= n; i++)
   {
       for(int j = 1; j <= m; j++)
            scanf("%d", &a[i][j]);
   }
    cout << solve() << endl;
    return 0;
}

把相交的情况设置为非法，然后进行求解。

#include <bits/stdc++.h>
#include <cstdio>
using namespace std;
#define N 55
int a[N][N];
int dp[N * 2][N][N];
int n, m;
int dx[4] = {0, 0, -1, -1};
int dy[4] = {-1, 0, -1, 0};
int solve()
{
    for(int k = 2;  k <= n + m; k++)
    {
        for(int i = 1; i < k && i <= n; i++)
        {
            for(int j = 1; j < k && j <= n; j++)
            {
                int maxv = 0;
                for(int p = 0; p < 4; p++)
                {
                    int ni = i + dx[p];
                    int nj = j + dy[p];
                    maxv = max(maxv, dp[k - 1][ni][nj]);
                }
                if(k == 2 && i == 1 && j == 1 || k == n + m && i == n && j == n) 
                    dp[k][i][j] = maxv;
                else if(i == j) dp[k][i][j] = -0x3f3f3f3f;
                else dp[k][i][j] = maxv + a[i][k - i] + a[j][k - j];
            }
        }
    }
    return dp[n+m][n][n];
}
int main()
{
    scanf("%d%d", &n, &m);
   for(int i = 1; i <= n; i++)
   {
       for(int j = 1; j <= m; j++)
            scanf("%d", &a[i][j]);
   }
    cout << solve() << endl;
    return 0;
}

最长上升子序列

AcWing1014. 登山

五一到了，ACM队组织大家去登山观光，队员们发现山上一共有N个景点，并且决定按照顺序来浏览这些景点，即每次所浏览景点的编号都要大于前一个浏览景点的编号。

同时队员们还有另一个登山习惯，就是不连续浏览海拔相同的两个景点，并且一旦开始下山，就不再向上走了。

队员们希望在满足上面条件的同时，尽可能多的浏览景点，你能帮他们找出最多可能浏览的景点数么？

输入格式

第一行包含整数N，表示景点数量。

第二行包含N个整数，表示每个景点的海拔。

输出格式

输出一个整数，表示最多能浏览的景点数。

数据范围

2≤N≤1000

输入样例：

8
186 186 150 200 160 130 197 220

输出样例：

题解

三大条件：

按照顺序来浏览这些景点（必须是子序列）
不连续浏览海拔相同的两个景点
一旦开始下山，就不再向上走了

单独看2不好操作，把2与3结合，得到：路线形状为^的左边严格单调递增，右边严格单调递减的路线。

可以枚举顶点的位置，从1到n

在顶点为某一个位置时，左右的最大值并没有关联，所以可以单独求得最大值然后相加。

如果令顶点在一个位置，求解一次，花费 $n^2$

求解多次花费貌似是 $n^3$ ，但是动态规划的过程量也已经求解，所以共需要 $n^2$ 可以求解本题。

#include <bits/stdc++.h>
using namespace std;
#define N 1020
int a[N];
int dp1[N];
int dp2[N];
int main()
{
    int n;
    cin >> n;
    for(int i = 1; i <= n; i++) scanf("%d", a+i);
    for(int i = 1; i <= n; i++){
        int t = 0;
        for(int j = 1; j < i; j++){
            if(a[j] < a[i]) t = max(dp1[j], t); 
        }
        dp1[i] = 1 + t;
    }
    // BUG 记录：我这里这一个是从左边开始，以f[i]为结尾的最长递减子序列
    // for(int i = 1; i <= n; i++){
    //     int t = 0;
    //     for(int j = 1; j < i; j++){
    //         if(a[j] > a[i]) t = max(t, dp2[j]);
    //     }
    //     dp2[i] = t + 1;
    // }
    for(int i = n; i >= 1; i--){
        int t = 0;
        for(int j = n; j > i; j--){
            if(a[i] > a[j]) t = max(t, dp2[j]);
        }
        dp2[i] = t + 1;
    }
    int ans = 0;
    for(int i = 1; i <= n; i++){
        ans = max(dp1[i] + dp2[i] - 1, ans);
    }
    printf("%d\n", ans);
    return 0;
}

AcWing1012. 友好城市

Palmia国有一条横贯东西的大河，河有笔直的南北两岸，岸上各有位置各不相同的N个城市。

北岸的每个城市有且仅有一个友好城市在南岸，而且不同城市的友好城市不相同。

每对友好城市都向政府申请在河上开辟一条直线航道连接两个城市，但是由于河上雾太大，政府决定避免任意两条航道交叉，以避免事故。

编程帮助政府做出一些批准和拒绝申请的决定，使得在保证任意两条航线不相交的情况下，被批准的申请尽量多。

输入格式

第1行，一个整数N，表示城市数。

第2行到第n+1行，每行两个整数，中间用1个空格隔开，分别表示南岸和北岸的一对友好城市的坐标。

输出格式

仅一行，输出一个整数，表示政府所能批准的最多申请数。

数据范围

1≤N≤5000
0≤xi≤10000

输入样例：

输出样例：

由于这一道题目给的是精确的数字，我们可以进行模糊化处理：

每一个城市的具体坐标并不影响是否交叉，所以我仅仅关心他们的相对左右有关新。

我们应该按照顺序进行寻找规律（下面的从小到大）

进行试探。选择了南北两个城市，那么我的其他选择只能是新选择的两个城市在已经选择城市的同一侧。

类似于最长上升子序列。

证明充分必要（容易证明）

这里的对应关系可以使用pair进行描述

代码

#include <bits/stdc++.h>
using namespace std;
#define N 5020
typedef pair<int, int> PII;
PII a[N];
int dp[N];
int n;
int main()
{
    scanf("%d", &n);
    for(int i = 1; i <= n; i++)
    {
        scanf("%d%d", &a[i].first, &a[i].second);
    }
    sort(a+1, a+1+n);
    for(int i = 1; i <= n; i++)
    {
        dp[i] = 1;
        for(int j = 1; j < i; j ++){
            if(a[j].second < a[i].second)
                dp[i] = max(dp[i], dp[j] + 1);
        }
    }   
    int ans = 0;
    for(int i = 1; i <= n; i++)
    {
        ans = max(ans, dp[i]);
    }
    printf("%d\n", ans);
    return 0;
}

1010. 拦截导弹

某国为了防御敌国的导弹袭击，发展出一种导弹拦截系统。

但是这种导弹拦截系统有一个缺陷：虽然它的第一发炮弹能够到达任意的高度，但是以后每一发炮弹都不能高于前一发的高度。

某天，雷达捕捉到敌国的导弹来袭。

由于该系统还在试用阶段，所以只有一套系统，因此有可能不能拦截所有的导弹。

输入导弹依次飞来的高度（雷达给出的高度数据是不大于30000的正整数，导弹数不超过1000），计算这套系统最多能拦截多少导弹，如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。

输入格式

共一行，输入导弹依次飞来的高度。

输出格式

第一行包含一个整数，表示最多能拦截的导弹数。

第二行包含一个整数，表示要拦截所有导弹最少要配备的系统数。

数据范围

雷达给出的高度数据是不大于 30000 的正整数，导弹数不超过 1000。

输入样例：

389 207 155 300 299 170 158 65

输出样例：

6
2

贪心法也可以使用过反证法：
假设贪心不是最优解，但是最后可以把贪心进行调整，使得等于最优解。故假设错误，贪心是最优解。

调整法的精髓：

在保证答案不发生变化的情况下，从最后一个不一样的地方一步一步调整，由于序列是有限的，所以最终可以得到最优解。

到最后的时候，这种贪心方法恰好是求解最长上升子序列的方法（贪心做法）。

所以等价于求解最长上升子序列。

187. 导弹防御系统

为了对抗附近恶意国家的威胁，R 国更新了他们的导弹防御系统。

一套防御系统的导弹拦截高度要么一直 严格单调 上升要么一直 严格单调 下降。

例如，一套系统先后拦截了高度为 3 和高度为 4 的两发导弹，那么接下来该系统就只能拦截高度大于 4 的导弹。

给定即将袭来的一系列导弹的高度，请你求出至少需要多少套防御系统，就可以将它们全部击落。

输入格式

输入包含多组测试用例。

对于每个测试用例，第一行包含整数 n，表示来袭导弹数量。

第二行包含 n个不同的整数，表示每个导弹的高度。

当输入测试用例 n=0 时，表示输入终止，且该用例无需处理。

输出格式

对于每个测试用例，输出一个占据一行的整数，表示所需的防御系统数量。

数据范围

1≤n≤50

输入样例：

5
3 5 2 4 1
0

输出样例：

样例解释

对于给出样例，最少需要两套防御系统。

一套击落高度为 3,4 的导弹，另一套击落高度为 5,2,1的导弹。

题解（DFS）

参考上一道题目的贪心策略，但是这里对于每一个点具有两种选择：要么上升，要么下降。所以在某一个地方就必须考虑两个情况，所以采用DFS。

时间复杂度：由于题目中的数字全部不一样，所以每一个系统至少可以干掉两个。所以最坏的是 $2^{25} = 33,554,432$ .在实际的情况下，ans肯定更小，这时候由于第一句的剪枝，所以时间复杂度是可以过去的。

DFS+剪枝

#include <bits/stdc++.h>
using namespace std;
#define N 55
int n;
int a[N], up[N], down[N];
int ans = 0;
void dfs(int u, int su, int sd)
{
    if(su + sd >= ans) return;// 剪枝
    if(u > n) {
        ans = min(ans, su+sd);
        return;
    }
    int k;
    int tmp;
    k = 1;
    while(k <= su && up[k] >= a[u]) k++;
    //k可能大于su，但是正好相当于后面加了一个
    tmp = up[k];
    up[k] = a[u];
    if(k > su) dfs(u + 1, su+1, sd);
    else dfs(u + 1, su, sd);
    up[k] = tmp;

    k = 1;
    while(k <= sd && down[k] <= a[u]) k++;
    tmp = down[k];
    down[k] = a[u];
    if(k > sd) dfs(u+1, su, sd+1);
    else dfs(u + 1, su, sd);
    down[k] = tmp;
}
int main()
{
    while(scanf("%d", &n), n){
        for(int i = 1; i <= n; i++) scanf("%d", a+i);
        ans = n;//其实是(n+1)/2级别的
        dfs(1, 0, 0);
        printf("%d\n", ans);
    }
  

    return 0;
}

题解（迭代加深）

对于深度优先，如果答案在很浅的部位，但是整个搜索树过于深，那么就会寄掉。

但是对于广度优先，本来挺好，但是在队列里面存储太多的元素，到时爆。同时，广度优先也不容易存储数据。同时还不容易剪枝

对于迭代加深，就是深度与广度的完美结合！

有着广搜的搜索浅层的时间复杂度
不会爆空间
容易利用系统所给的栈来进行存储
还可以剪枝

#include <bits/stdc++.h>
using namespace std;
#define N 55
int n;
int a[N];
int up[N];
int down[N];

bool dfs(int ans, int u, int su, int sd)
{
    if(su + sd > ans) return false;
    if(u > n) return true;
  
    int k, tmp;
    k = 1;
    while(k <= su && up[k] >= a[u]) k++;
    tmp = up[k];
    up[k] = a[u];
    /*
惊天动地大BUG：
如果这样：
if(k > su) if(dfs(ans, u+1, su+1, sd)) return true;
else if(dfs(ans, u+1, su, sd)) return true;
那么下面的else是与第一行的第二个if进行配对！！！
    */
    if(k > su) {if(dfs(ans, u+1, su+1, sd)) return true;}
    else if(dfs(ans, u+1, su, sd)) return true;
    up[k] = tmp;
  
    k = 1;
    while(k <= sd && down[k] <= a[u]) k++;
    tmp = down[k];
    down[k] = a[u];
    if(k > sd) {if(dfs(ans, u+1, su, sd+1)) return true;}
    else if(dfs(ans, u+1, su, sd))return true;
    down[k] = tmp;
    return false;
}

int main()
{
    while(scanf("%d", &n), n)
    {
        for(int i = 1; i <= n; i++){
            scanf("%d", a+i);
        }
        int ans = 1;
        while(1){
            if(dfs(ans, 1, 0, 0)){
                break;
            }
            else{
                ans ++;
            }
        }
        printf("%d\n", ans);
    }
    return 0;
}

272. 最长公共上升子序列

熊大妈的奶牛在小沐沐的熏陶下开始研究信息题目。

小沐沐先让奶牛研究了最长上升子序列，再让他们研究了最长公共子序列，现在又让他们研究最长公共上升子序列了。

小沐沐说，对于两个数列 A 和 B，如果它们都包含一段位置不一定连续的数，且数值是严格递增的，那么称这一段数是两个数列的公共上升子序列，而所有的公共上升子序列中最长的就是最长公共上升子序列了。

奶牛半懂不懂，小沐沐要你来告诉奶牛什么是最长公共上升子序列。

不过，只要告诉奶牛它的长度就可以了。

数列 A 和 B 的长度均不超过 3000。

输入格式

第一行包含一个整数 N，表示数列 A，B 的长度。

第二行包含 N 个整数，表示数列 A。

第三行包含 N 个整数，表示数列 B。

输出格式

输出一个整数，表示最长公共上升子序列的长度。

数据范围

1≤N≤3000,序列中的数字均不超过 $2^{31}-1$ 。

输入样例：

4
2 2 1 3
2 1 2 3

输出样例：

题解

是最长上升子序列以及最长公共子序列的完美结合。

状态表示

f[i][j]表示a序列中的前 i 项以及b序列中的前 j 项，并且以b[j]结尾（为了便于求解上升。但是并不需要a[i]结尾，这是因为是公共子序列，所以是相等）的所有公共上升子序列

状态属性

最大值

状态转移（对于f[i][j]）

当f[i][j]的子序列中并不包含a[i]，那么显然有：f[i][j] = f[i-1][j]
当f[i][j]的子序列中包含a[i]：
根据状态表示得知：f[i][j]的子序列中包含b[i].所以这一种情况的条件是a[i] == b[j]
然后枚举a[i-1][k]，如果可以，那么取最小值。

详细见代码：

for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= n; j++)
        {
            f[i][j] = f[i-1][j];
            if(a[i] == b[j])
            {
                f[i][j] = max(f[i][j], 1);
                for(int k = 1; k < j; k++)
                {
                    if(a[i] > b[k]) f[i][j] = max(f[i][j], f[i][k] + 1);
               }
            }
        }
    }

但是需要进行优化：求最大值的时候并没有必要每一次都扫一遍！

for(int i = 1; i <= n; i++)
    {
	int maxv = 0;
        for(int j = 1; j <= n; j++)
        {
            f[i][j] = f[i-1][j];
            if(a[i] == b[j])
            {
                f[i][j] = max(f[i][j], 1);
		f[i][j] = max(f[i][j], maxv+1);
		if(b[j] < a[i]) maxv = max(maxv, f[i][j]);
            }
        }
    }

最终代码

#include <bits/stdc++.h>
using namespace std;
#define N 3020
int a[N], b[N], f[N][N];
int n;
int main()
{
    scanf("%d", &n);
    for(int i = 1; i <= n; i++) scanf("%d", a+i);
    for(int i = 1; i <= n; i++) scanf("%d", b+i);

    for(int i = 1; i <= n; i++)
    {
	    int maxv = 0;
        for(int j = 1; j <= n; j++)
        {
            f[i][j] = f[i-1][j];
            if(a[i] == b[j])
            {
                f[i][j] = max(f[i][j], 1);
		        f[i][j] = max(f[i][j], maxv+1);
            }
	        if(b[j] < a[i]) maxv = max(maxv, f[i][j]);// 这个应该在if(a[i] == b[j])的外面
        }
    }

    int ans = 0;
    for(int i = 1; i <= n; i++){
        ans = max(f[n][i], ans);
    }
    printf("%d", ans);
    return 0;
}