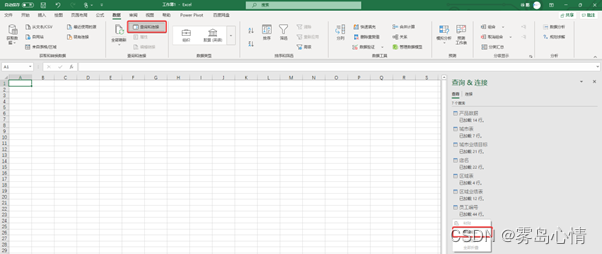
在实际的应用场景中，单一连接的场景非常少见。通常存在着两个或者两个以上的PowerQuery数据源。在这类场景下一个一个的复制数据源效率非常低下，是否存在更加有效率的数据源复制方式呢？接下来分享的连接组功能就是这样的概念。在PowerQuery中如果数据连接提供的分类比较多，例如有些数据来源于文件，有些数据来源于数据库。如果这些数据源混合在一起的话我们将无法实现非常清洗的分类和数据标记。PowerQuery的数据源分组功能提供了依据不同的目标和功能进行数据源分组，实现相对比较清晰功能标记。在Excel创建数据源分组非常简单，创建的分组里面可以没有数据源连接。图为创建数据源分组的方法。需要清楚的概念是，我们进行数据源连接复制复制过去的是连接字符串，并不意味着可以顺利的访问到数据源。

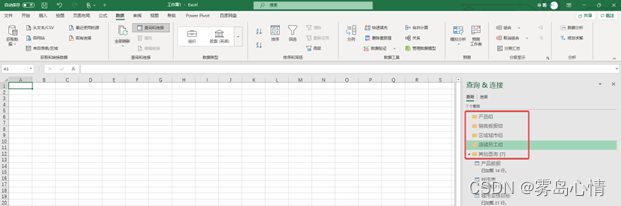
弹出的窗口中填入需要构建的连接组名称，图为完成后的数据连接组

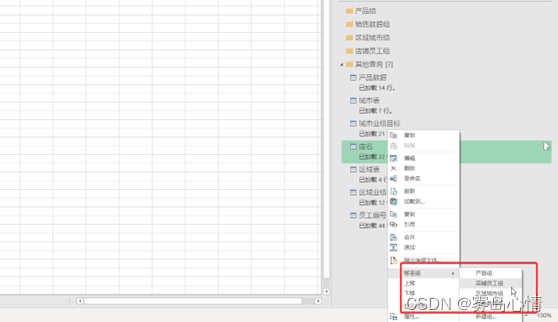
完成最终的数据连接组之后，接下来就需要将相应的数据连接放入相应的连接组中来实现数据连接的归类

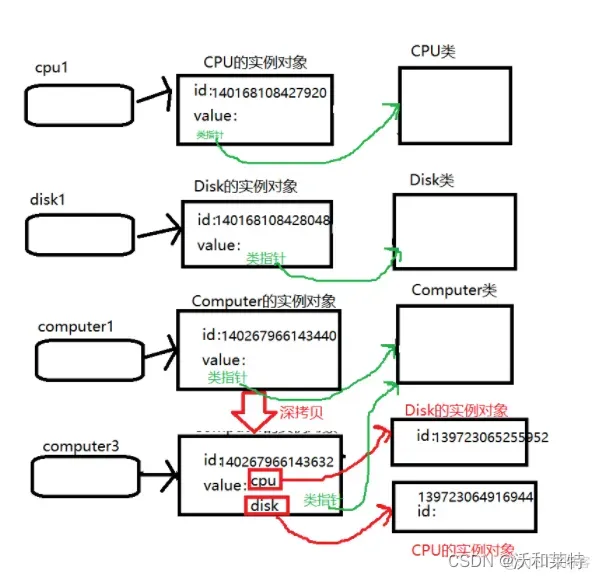
完成最终的数据源组建立和数据源移入到相应的数据源组之后，最终的数据源组和数据源之间的关系如图。

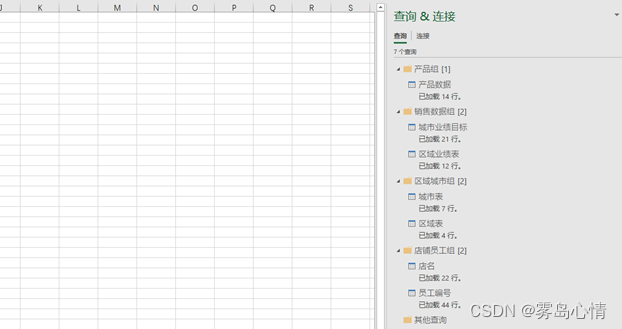
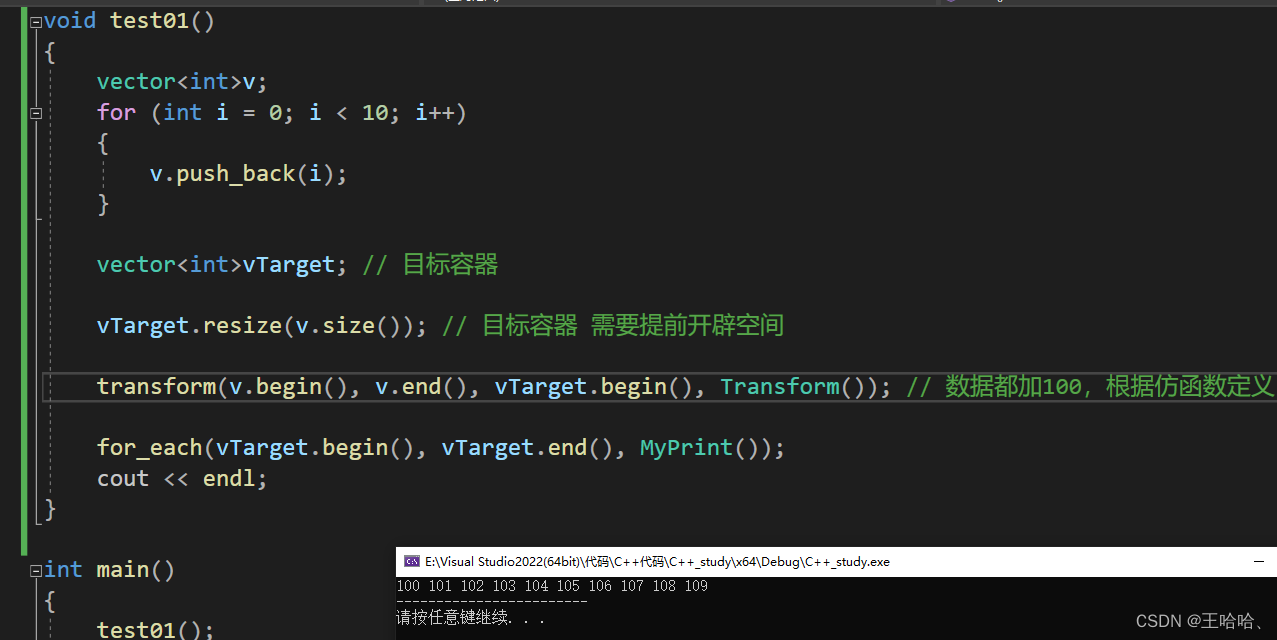
构建完成数据源组之后，我们可以将导入的数据源连接统一的进行复制，避免因为太多的数据源而产生的大量重复操作，图为基于数据源组的复制操作

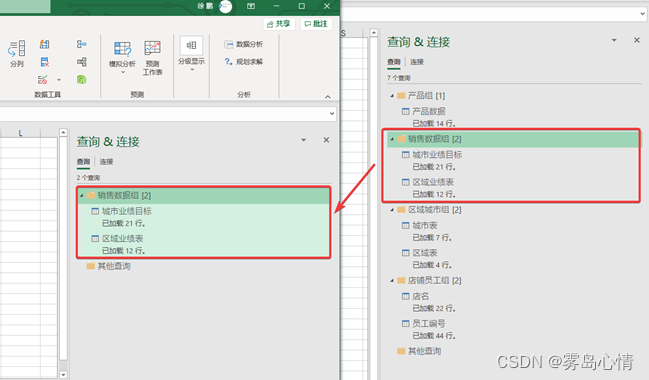
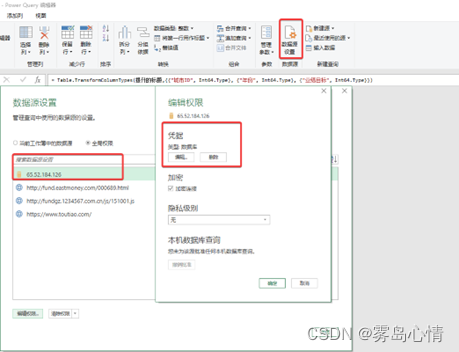
在进行数据源组复制过程中，有一类场景需要特别注意，如果这一类数据是带需要进行访问权限的。例如我们访问共享目录中的数据源，或者访问的是SQL Server或者MYSQL 这样的需要凭据进行验证的数据，我们需要在进行数据源获取数据之前构建相应的访问凭据。