个人博客

• 密码技术扫盲：对称加密
• 🎯 密码技术扫盲：非对称加密
• 密码技术扫盲：认证

在上一篇对称加密的介绍中，我们了解到对明文的加密需要使用到密钥，而解密时也必须用到同一把密钥，也就是说发送者和接收者都需要有这把密钥，都可以做加密、解密操作。

我们想要安全地传递信息，所以选择使用密钥对信息进行加密后再传送，这样即使在传递过程被窃听，也不会泄露具体内容。现在接收者收到的是密文，需要经过解密才能得到具体内容，解密需要密钥，问题来了，接收者怎么知道密钥？或者说，双方如何知道同一个密钥？密钥在发送者或接收者手上，那么必然有一个将密钥从一方转移到另一方的过程。到这里，问题就转化为如何安全地配送密钥 —— 称为密钥配送问题。

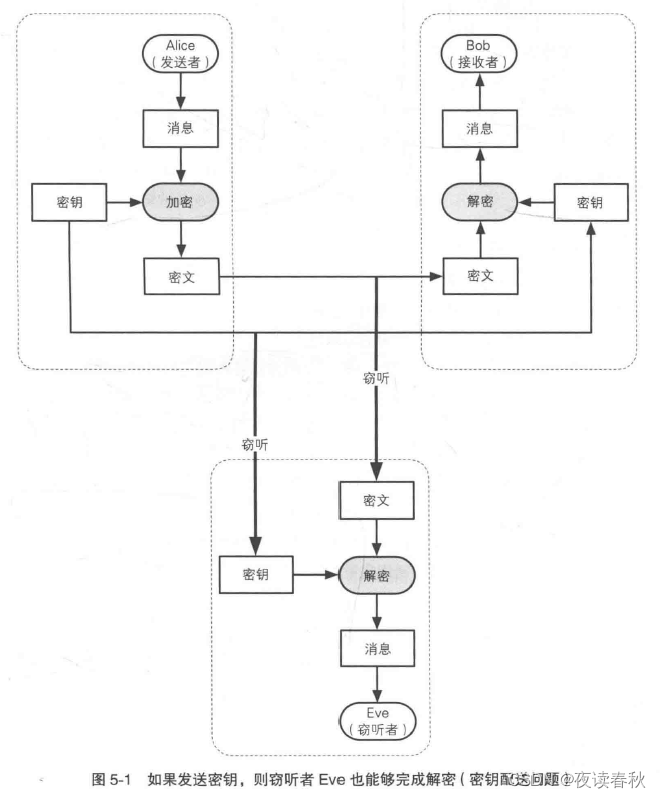
这里，两个问题是同质的，只是需要应对的问题规模不一样，问题规模的缩小带来了可操作空间。解决密钥配送问题一般有 4 种方案：

• 事先共享；
• 通过密钥配送中心交换；
• 通过 Diffie-Hellman 算法交换；
• 通过非对称加密算法交换。

非对称加密的解决方式非常巧妙——也是其名称的由来，非对称加密算法有两个唯一成对的密钥，一个是公钥，对外公开的，一个是私钥，对外保密的，在非对称加密中用一个密钥加密的信息只有对应的另一个密钥才能解密，也就是说，使用公钥加密的信息只有拥有私钥的一方可以解密。任何人拿到公钥，也无法解密被公钥加密的信息，如此就不用保障公钥配送的安全性了。唯一的问题是，如何确认公钥的合法性，确保不被中间人攻击。

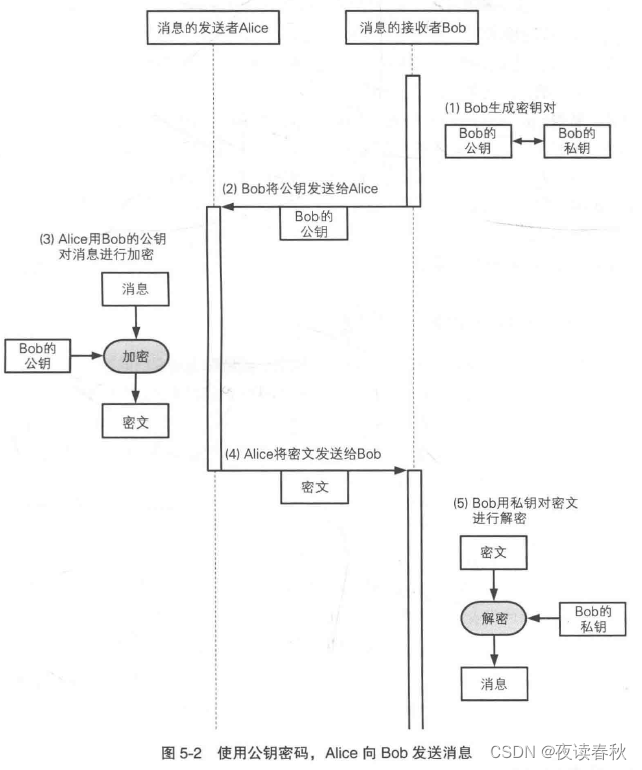
非对称加密算法的代表是 RSA，目前被广泛应用于各种场景，随着近年对个人隐私的关注度提高，聊天工具中又兴起采用非对称加密保障用户聊天内容机密的应用场景，称为 E2EE。和对称加密依赖于异或运算不同，RSA 的加解密机制主要依赖于取模运算（mod）—— 除法之后求余数。

• RSA 加密：密文 = 明文E mod N
• RSA 解密：明文 = 密文D mod N

以上两个就是 RSA 算法加解密的公式，其中明文、密文都是数字，公钥就是（E，N）组合，私钥就是（D，N）组合。

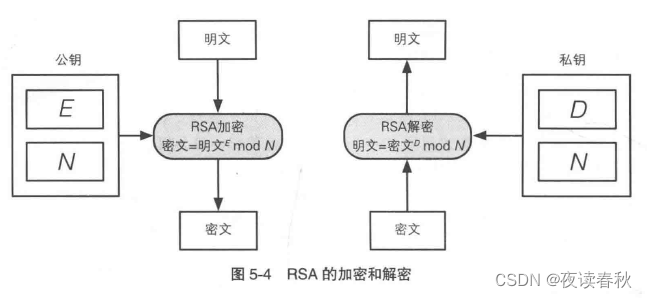
下面看看 E、D、N 是如何计算出来的：

• ① N = p * q， p、q 为两个挑选出的质数
• ② L = lcm (p-1, q-1)， lcm 表示求最小公倍数，求 E、D 时需要
• ③ gcd (E, L) = 1, 1 < E < L， gcd 表示求最大公约数
• ④ (E * D) mod L = 1, 1 < D < L

因为公钥就是（E，N），是公开的，只要求出 D，私钥就被破解了。计算 D 需要知道 L，计算 L 需要知道 p、q，N 是知道的，所以问题核心就是将 N 质因数分解得到 p、q。目前没有发现对大整数进行质因数分解的高效算法，也尚未证明质因数分解是否真是非常困难的问题，甚至不知道是否存在一种分解质因数的简单方法，在现实的时间里，无法对 N 进行质因数分解。RSA 的安全性就在这里。

非对称加密虽然非常优秀，但在采用同等机密性密钥条件下，非对称加解密效率只有对称加密的几百分之一，所以非对称加密算法并不能取代对称加密算法。所以在类似 TLS 这样的混合场景中，会采用非对称加密来传递对称密钥，使用对称加密来加密应用数据，同时兼顾安全性和效率。

在 TLS 中，传递密钥可以选择使用 RSA 进行加密传递，还有一种选择是 Diffie-Hellman 算法，Diffie-Hellman 也很巧妙，有必要写一下：

• ① 选择一个非常大的质数 P 及其生成元 G（G1-GP-1 mod P 要能映射出所有 1 到 P-1 这 P-1 个数字），P、G 公开
• ② 发送端生成一个随机数 A，不公开，1 < A < P-2
• ③ 接收端生成一个随机数 B，不公开，1 < B < P-2
• ④ 发送端计算 GA mod P 给接收端，接收端计算密钥 (GA mod P)B mod P
• ⑤ 接收端计算 GB mod P 给发送端，发送端计算密钥 (GB mod P)A mod P
• ⑥ 最后发送端和接收端都得到密钥 GA*B mod P

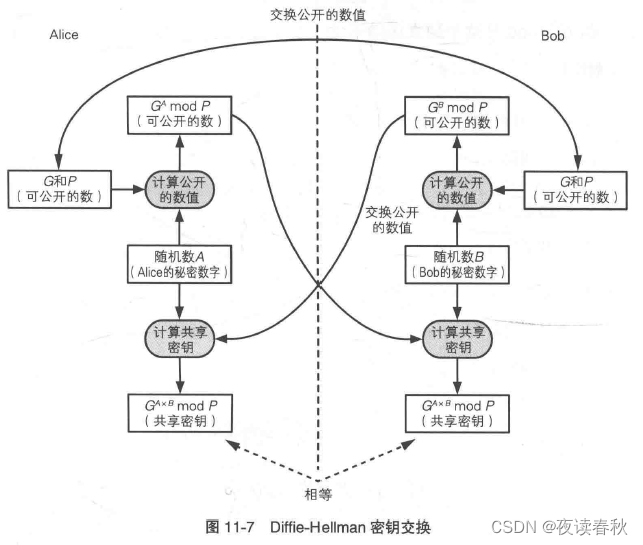
P、G、GA mod P、GB mod P 是公开的，只要能计算出 A 或者 B，算法就被破解了，但目前还没有找到方法 —— 称为有限域的离散对数问题，Diffie-Hellman 的安全性就在这里。这种交换思想值得借鉴，可以用于应用层在 tls 之外再单独和前端约定自己的数据加密密钥。

---

参考

• 《图解密码学》