常见损失函数

引言

无论在机器学习还是深度领域中,损失函数都是一个非常重要的知识点。损失函数（Loss Function）是用来估量模型的预测值 f(x) 与真实值 y 的不一致程度。我们的目标就是最小化损失函数，让 f(x) 与 y 尽量接近。通常可以使用梯度下降算法寻找函数最小值。

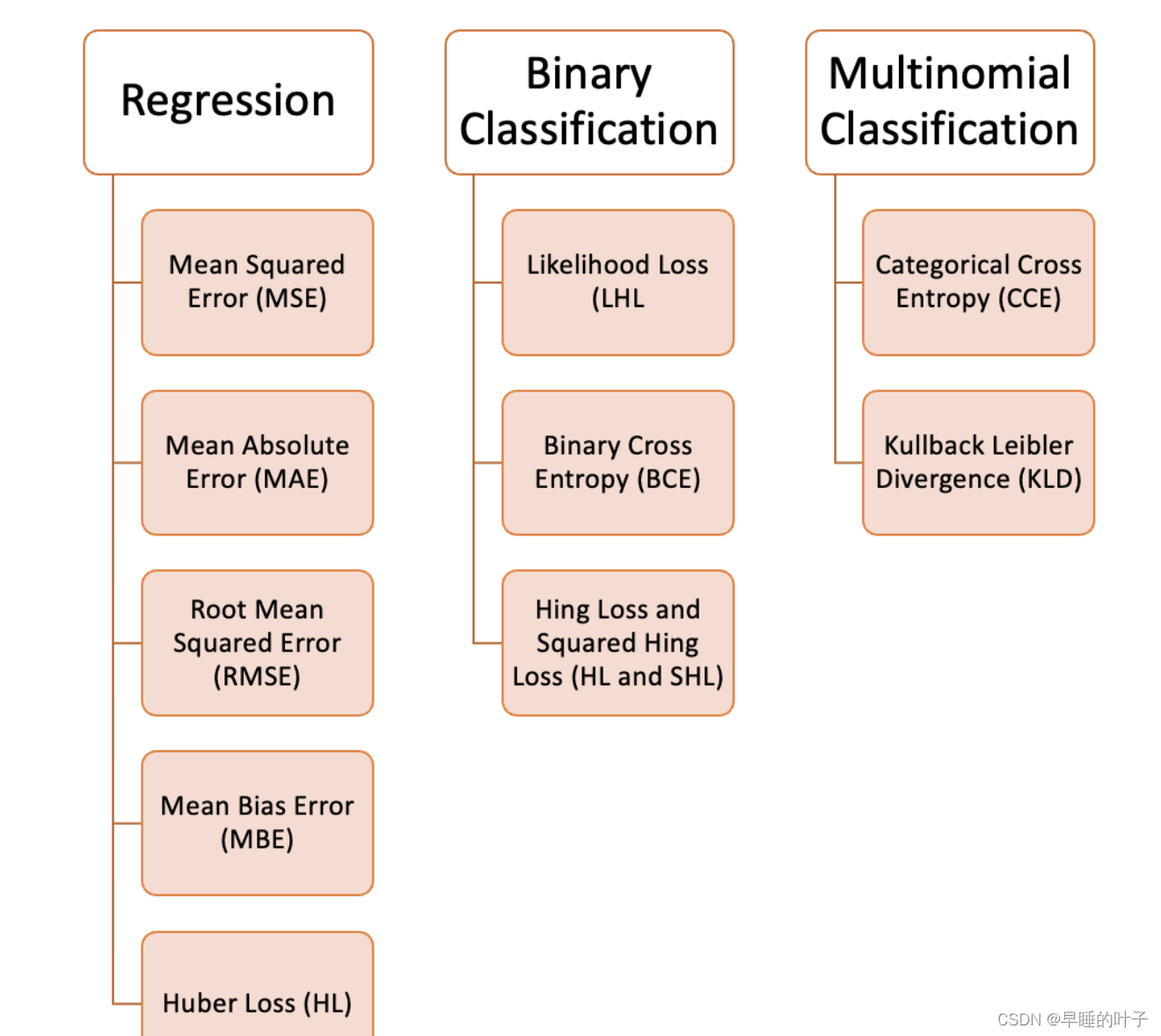
损失函数有许多不同的类型，没有哪种损失函数适合所有的问题，需根据具体模型和问题进行选择。一般来说，损失函数大致可以分成两类：回归（Regression）和分类（Classification）。

回归

回归模型中的三种损失函数包括：均方误差（Mean Square Error）、平均绝对误差（Mean Absolute Error，MAE）、Huber Loss。

1. 均方差

均方误差（Mean Square Error）是回归问题最常用的损失函数。回归问题解决的是对具体数值的
预测，比如房价预测、销量预测等。这些问题需要预测的不是一个事先定义好的类别，而是一个任意实
数。均方误差定义如下：

均方误差指的就是模型预测值 f(x) 与样本真实值 y 之间距离平方的平均值

def mse(p, y):
    return np.mean(np.square(p - y))

2.平均绝对误差(MAE)

与均方误差相似，平均绝对误差通常用于连续变量值的预测。

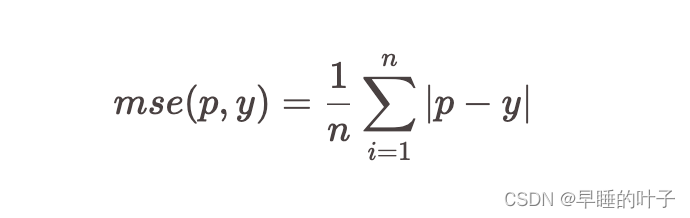
def mae(p, y):
    return np.mean(np.abs(p - y))

3. 均方根误差(RMSE)

平均偏差误差(MBE)
Huber损失

4. 交叉熵

交叉熵（Cross Entropy）表征两个概率分布之间的距离，交叉熵越小说明二者分布越接近，是分
类问题中使用较广泛的损失函数

分类

二分类

• 最大似然损失(Likelihood Loss/LHL)
• 二元交叉熵(BCE)
• Hinge Loss 和 Squared Hinge Loss (HL and SHL)

多分类

• 交叉熵（CE）
• Kullback-Leibler 散度 (KLD)

---

参考：

• AI基础：机器学习的损失函数
• https://www.51cto.com/article/716760.html
• 使用numpy实现各种损失函数