优化器

1. 引言

优化算法可以分成一阶优化和二阶优化算法，其中一阶优化就是指的梯度算法及其变种，而二阶优
化一般是用二阶导数（Hessian 矩阵）来计算，如牛顿法，由于需要计算Hessian阵和其逆矩阵，计算
量较大，因此没有流行开来。这里主要总结一阶优化的各种梯度下降方法。

深度学习优化算法经历了SGD -> SGDM -> NAG ->AdaGrad -> AdaDelta -> Adam -> Nadam
这样的发展历程。

class Adadelta: Optimizer that implements the Adadelta algorithm.

class Adagrad: Optimizer that implements the Adagrad algorithm.

class Adam: Optimizer that implements the Adam algorithm.

class Adamax: Optimizer that implements the Adamax algorithm.

class Ftrl: Optimizer that implements the FTRL algorithm.

class Nadam: Optimizer that implements the Nadam algorithm.

class Optimizer: Abstract optimizer base class.

class RMSprop: Optimizer that implements the RMSprop algorithm.

class SGD: Gradient descent (with momentum) optimizer.

1. SGD

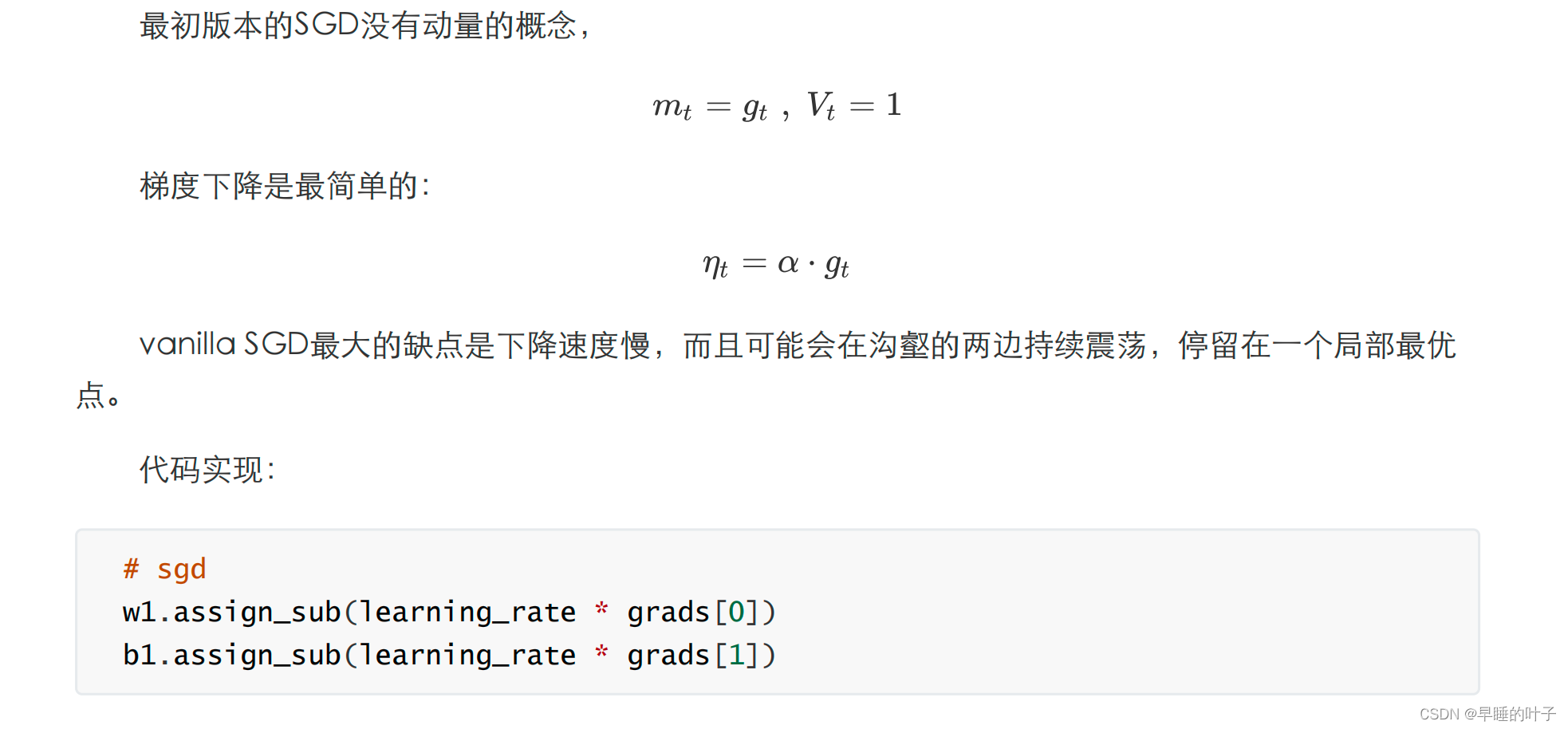
1.1 vanilla SGD

1.2 SGD with Momentum

1.3 SGD with Nesterov Acceleration

2. AdaGrad

TensorFlow API: tf.keras.optimizers.Adagrad

3. RMSProp

tf.keras.optimizers.RMSprop

4. AdaDelta

tf.keras.optimizers.Adadelta

5. Adam

TensorFlow API: tf.keras.optimizers.Adam

优化器选择

很难说某一个优化器在所有情况下都表现很好，我们需要根据具体任务选取优化器。一些优化器在
计算机视觉任务表现很好，另一些在涉及RNN网络时表现很好，甚至在稀疏数据情况下表现更出色。
总结上述，基于原始SGD增加动量和Nesterov动量，RMSProp是针对AdaGrad学习率衰减过快
的改进，它与AdaDelta非常相似，不同的一点在于AdaDelta采用参数更新的均方根（RMS）作为分
子。Adam在RMSProp的基础上增加动量和偏差修正。如果数据是稀疏的，建议用自适用方法，即
Adagrad, RMSprop, Adadelta, Adam。RMSprop, Adadelta, Adam 在很多情况下的效果是相似
的。随着梯度变的稀疏，Adam 比 RMSprop 效果会好。总的来说，Adam整体上是最好的选择。
然而很多论文仅使用不带动量的vanilla SGD和简单的学习率衰减策略。SGD通常能够达到最小
点，但是相对于其他优化器可能要采用更长的时间。采取合适的初始化方法和学习率策略，SGD更加可
靠，但也有可能陷于鞍点和极小值点。因此，当在训练大型的、复杂的深度神经网络时，我们想要快速
收敛，应采用自适应学习率策略的优化器。
如果是刚入门，优先考虑Adam或者SGD+Nesterov Momentum。
算法没有好坏，最适合数据的才是最好的，永远记住：No free lunch theorem。

出处

SGD（1952）：https://projecteuclid.org/euclid.aoms/1177729392
SGD with Momentum（1999）：https://www.sciencedirect.com/science/article/abs/pii/ S0893608098001166 SGD with Nesterov Acceleration（1983）：由Yurii Nesterov提出
AdaGrad（2011）: http://www.jmlr.org/papers/volume12/duchi11a/duchi11a.pdf
RMSProp（2012）: http://www.cs.toronto.edu/~tijmen/csc321/slides/lecture_slides_lec6. pdf
AdaDelta（2012）: https://arxiv.org/abs/1212.5701
Adam:（2014） https://arxiv.org/abs/1412.6980
（对上述算法非常好的可视化：https://imgur.com/a/Hqolp）