介绍

递归(DFS)是一个劲的往某一个方向搜索，而回溯算法建立在 DFS 基础之上的，但不同的是在搜索过程中，达到结束条件后，恢复状态，回溯上一层，再次搜索。因此回溯算法与 DFS 的区别就是有无状态重置。

伪代码

    List<List<T>> res = new ArrayList<>(); //记录答案
    List<T> path = new ArrayList<>();  //记录路径
    public void backtracking(参数列表){
        //  可以有，也可不写，毕竟我们for循环也是有
        if(终止条件){
            //收集结果
            //res.add();
            return;
        }
        
        for(元素集){
            // 处理结点
            
            // 递归
            
            // 回溯操作 ——> 撤销处理结点的情况
            // 所以我们是否存在回溯，都取决于我们是否多次处理了结点，他们两个要匹配
            
        }
    }

例题：

给你一个无重复元素的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的所有不同组合，并以列表形式返回。你可以按任意顺序返回这些组合。

candidates 中的同一个数字可以无限制重复被选取。如果至少一个数字的被选数量不同，则两种组合是不同的。

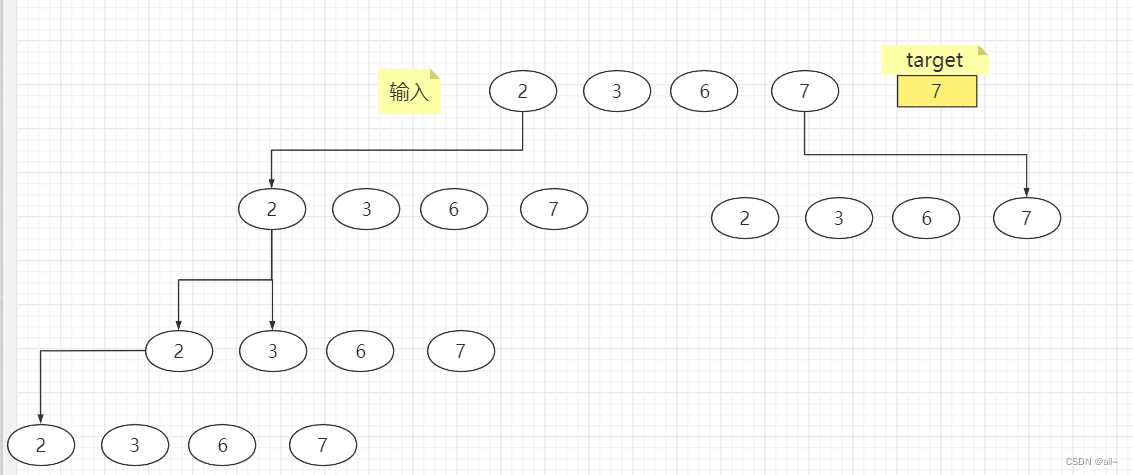
请添加图片描述

解释：

简单来说，就是递归，回溯是一个暴力手段，找得到就存，找不到的时候一旦到达叶子底部就回退路径，换一条路，其核心就是他的模板内容

	List<List<Integer>> result = new ArrayList(); // 保存结果
	/*
	 保存路径 ->但是保存的时候要按着这个path重新new一个，引用对象，我们不改变对象
	 地址也就不变，但是改变这个对象的值，并不会影响对象地址，事实上我们时刻在改变
	 这个path集合元素，所以当元素条件符合时我们new一个出来让他保存这个结果，放到result中
	 让path继续运动
	*/
	List<Integer> path = new ArrayList();		
	public void backtracking(int[] temp,int target,int sum,int start ){
		// 结束条件
        if(sum == target){
            res.add(new ArrayList(path));
            return;
        }
        
        for(int i = 0 ; i < temp.length ; i++){
            int tt = temp[i] + sum ; 
            if(tt < target){
                // 处理结点
                path.add(temp[i]);
                //递归
                backtracking(temp.target,tt,i);
                // 回溯操作 ——> 撤销处理结点的情况
                path.remove(path.size()-1);
            }else break;
        }
    }
	public List<List<Integer>> combinationSum(int[] candidates, int target) {
        Arrays.sort(candidates);
        backtracking(candidates,0,target,0);
        return res;
    }

回溯算法中的优化

去重

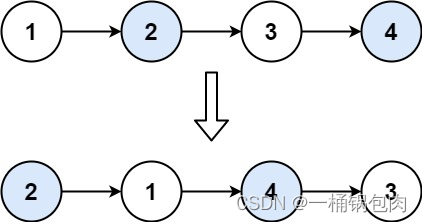
我们一般取得数据都是取得叶子结点上的值，所以只要我们每次保证，在有序的集合中，相同层级下取出的数据和上一次回溯的结果不同即可。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-aHunEUW9-1671289185260)(算法总结/image-20220902210359548.png)]

以这个为例，我们第一次可以直接取到地，但是这个时候我们也获取的第一次回溯的结点：2，我们下次就不能再去取他，这样 1、1、x，x只能取2,3,4这样就保证在1、1开头的组合没有重复的组合，同理当层取完回溯之后我们1、1开头的数据就取完了，第二个结点就不能再去取1了同理，其它层也是如此理解。

伪代码

public static List<List<Integer>> res = new ArrayList<>(); // 所有的叶子结点数据
public static List<Integer> path = new ArrayList<>(); // 当前路径的值，其实是一个临时变量

public /* 你要返回的数据类型 */ solution(int[] nums){
    Arrays.sort(nums);//在去重之前我们要保证有序
    dsf(nums,0);
    
}

public void dsf(int[] nums ,int start ){
    
    if(/*满足要求，或者到达界限开始判断存储*/){
        // 自定义判断
        
        res.add(new ArrayList(path));
        return;
    }
    
    int temp = Integer.MAX_VALUE; // 用来记录回溯数据
    for (int i = start; i < nums.length; i++) {
        if (nums[i] == temp) { // 同级去下一个元素之前，不可以重复去取已经判断过的点了
            continue;
        }
        path.add(nums[i]);

        dsf(nums,i+1);

        temp = path.remove(path.size() - 1);
    }
}

剪枝

其实剪枝就是提前退出循环、或者递归，这里要自己按照题目要求增加 if语句，比如在一个有序集合中我们要的数据必须小于0，但是我们在下一个数据就取到了5，而且所以之后的数据也就不用在进行递归遍历了，没有意义。

大概就是这意思，剪枝一定要注意。他确实是一个优化的大手段。但是也要注意不要过分剪枝，导致数据缺失，这里就要求我们的 if语句判断必须严格，符合题意。

常见题型

求子集
全排列
…

子集例题

Leetcode78题

	/** 
	* 最终结果的保存
    */
	private static List<List<Integer>> result = new ArrayList<>();
	/** 解题思路
    我们常在进行数据添加的时机都会选择在，我们的终止条件，也就是最开始的 if () ... 中
    但是这样会导致我们，在回溯的时候少了一些点，例如 1 3 4 在 1 3 4 选择之后 我们下一个结果是 1 4
    因为我们在 1 3 4 确定之后 别忘了我们其实是在3的基础上判断，所以 i+1处理之后我们就回溯，自然就将3删除了
    显然我们忽略了 1 3 这个数据。
     所以我们现在不拖到最后，在我们纵深的同时，也添加数据。这样我们不会漏掉一个数据，
     */
    public static void dsf(int[] nums, int start,List<Integer> path) {
        // result.add(new ArrayList<>(path));
        // if (!path.isEmpty()) result.add(new ArrayList<>(path)); //如果需要的是非空子集
        if (!path.isEmpty() && path.size() != nums.length) result.add(new ArrayList<>(path)); //如果需要的是非空真子集}
        for (int i = start; i < nums.length; ++i) {
            path.add(nums[i]);
            dsf(nums, i + 1, path);
            path.remove(path.size() - 1);
        }
    }
     public List<List<Integer>> subsets(int[] nums) {
			dsf(nums,0,new ArrayList());
			  return result;
    }
 
    /** 解题思路
    同上，我们要是还是想着直接纵深，临时保存就行，直到我们当前状态无法选择，再将我们得到的路径保存下来
    问题我们也说过了，我们通用的模板有一个问题就是漏数据了，我们在结束点的数据会直接回退两次，会让我们少数据
    所以我们只需要补偿这时候的数据即可
    
     缺点：无法直接获取全部的子集，因为空集我们不能直接获取
     */
    public void dfs(int cur, int[] nums,List<Integer> path) {
        if (cur == nums.length) {
            result.add(new ArrayList<Integer>(path));
            return;
        }
        path.add(nums[cur]);
        dfs(cur + 1, nums, path);
        path.remove(path.size() - 1);
        dfs(cur + 1, nums, path); // 补偿回退过程中即将缺少的数据
         /** 解释
         例如 原本集合 {1 3 4}
         我们已经到了 1 3 4，到第一次回溯完成，我们得到了他的第一个子集，同时我们去除了 4
         如果我们直接结束 我们 path={1,3} 状态下的3也会被删除，直接进入{1,4}，
         因为我们是在{1,3}状态下，进入的下一状态，即 dsf ，我们处理完成，必然要回溯删除状态3
         所以我们在我们删除状态 4 的时候再次dsf,其实是我们对 3的补偿。
         */
    }

全排列例题

伪代码

	/** 解题思路
    前提: 不考虑去重问题
    全排列问题就是 我们每个结点都可能在当前位置，所以我们每次都需要重头遍历，
    但是当前元素有且仅有一次出现，我们不能重复取这个元素，这样导致元素全部重复

    所以相对于取集合问题，我们需要知道我们下一个的位置，这里我们则需要知道那些元素取过了即可.
    如果后期遇到重复元素我们，我们也有专门去重的技巧，我们只需要记录上一次回溯的元素，在下一次
    添加操作缓存的时候进行一下判断即可。具体翻一下上面去重的内容
     */
    public static void dsf(int[] nums, boolean[] map, List<Integer> path) {
        if (path.size() == nums.length) {
            result.add(new ArrayList<>(path));
            return;
        }
        for (int i = 0; i < nums.length; ++i) {
            if (!map[i]) {
                path.add(nums[i]);
                map[i] = true;
                dsf(nums,  map, path);

                map[i] = false;
                path.remove(path.size() - 1);
            }
        }
    }