CPOFDM-16QAM性能仿真,输出接收端的星座图

news2025/1/11 8:14:07

目录

1.算法描述

2.仿真效果预览

3.MATLAB核心程序

4.完整MATLAB

1.算法描述

        CP-OFDM（Cyclic Prefix Orthogonal Frequency Division Multiplexing，循环前缀正交频分复用）通信系统采用多个正交子载波（Orthogonalsub-Carrier）并行传输数据，可以高效传输数据并且有效对抗频率选择性衰落信道带来的影响。但是在数据传输过程中，对子载波的正交性有严苛的要求，所以CP-OFDM系统对载波及采样时钟的频率偏差（即频偏）非常敏感，必须通过频偏估计与纠正技术，使得频率偏差处于接收机可容忍范围内，从而保证数据的正确传输。
       CP-OFDM 技术利用多个平行窄带子载波来传输信息，而不使用单个宽带载波。该技术定义充分，已在 4G LTE 下行链路和Wi-Fi通信标准成功实施，因此也适合用于 5G NR 设计。

       不过，5G NR 上行链路还提供了一种不同的波形格式，这种波形格式类似 4G LTE 上行链路使用的波形模式⸺离散傅立叶变换扩频正交频分复用（DFT-S-OFDM）波形。DFT-S-OFDM 波形是一种 4G 采用的波形，结合了循环前缀正交频分复用和低峰均比（PAPR）的优点。DFTS-OFDM 波形对上行链路有帮助，对于高功率的 2 级功率应用或者当用户设备位于基站蜂窝的边缘位置，远离信号塔时，DFT-S-OFDM 可能是首选波形。

       在灵活性上，5G NR 提供的子载波间隔方案还超越了 LET 提供的固定 15 kHz 子载波间隔。5G NR 提供的子载波间隔包括 FR2，最大间隔达到 240 kHz。灵活的载波间隔可用于适当支持 5G NR 所需的多元化频带、频谱类型及部署模式。

        DFT-S-OFDM 非常类似于 LTE 上行链路使用的单频分复用接入（SCFDMA），CP-OFDM 非常类似于 LTE 下行链路使用的正交频分复用接入（OFDMA）。3GPP 之所以选择 CP-OFDM，原因如下：

CP-OFDM 能够面向复杂程度较低的接收器延展。

在一些最重要的 5G 性能指标上（例如：与多天线技术的兼容性），CP-OFDM 排名最高。

CP-OFDM 的时域控制良好，这一点对于低延时关键应用和时分双工（TDD）部署具有重要意义。``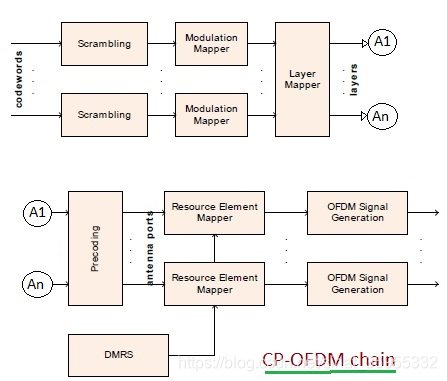图1 CP-OFDM链路

2.仿真效果预览

matlab2022a仿真结果如下：

 

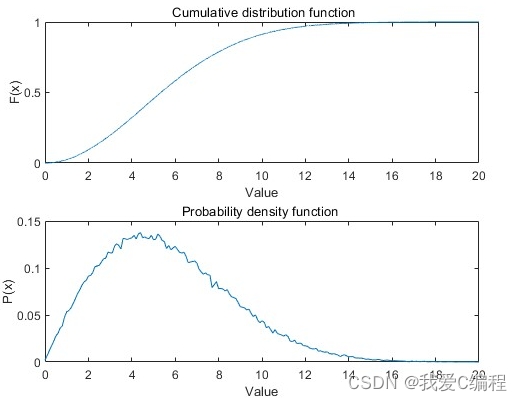
3.MATLAB核心程序

clc;
clear;
close all;
warning off;
addpath(genpath(pwd));
 
 
v1 = 1;
v2 = 3;
nBit = 1024*2;
lSymbol = 4;
nChannel = 4;
baseFreq = 100; % 1Hz
tSymbol = nChannel/baseFreq; % time for one symbol
nSymbol = nBit/(nChannel*lSymbol);
bitSequence = bit_generate(nBit);
 
mapQAM = mapping_16QAM(v1,v2);
 
for k = 1:nBit/lSymbol
    rInd = fix((k-1)/nChannel) +1;
    cInd = k-(rInd-1)*nChannel;
    fr = (k-1)*lSymbol +1;
    bSymbol(rInd,cInd).bit = bitSequence(fr:fr+lSymbol-1);  
end
 
fBase = 100; %100Hz for base frequence
fFirst = 200; %500Hz for first channel
Fs = 1024;
rTg = 1/8; %Ratio of guard 
Tsym = 1/fBase;
Tg = Tsym*rTg;
Tsig = nSymbol*(Tsym+Tg);
 
bSymbol = generateSymbolWave(bSymbol,mapQAM,fBase,fFirst,rTg,Fs);
 
sOFDM = [];
for k=1:nSymbol
    tmpSignal = 0;
    for j= 1:nChannel
        tmpSignal = tmpSignal + bSymbol(k,j).symbol;
    end
    sOFDM = [sOFDM tmpSignal];
end
 
%sOFDM is the signal CP-OFDM
% figure(1);
% dt = 1/(fBase*Fs);
% t=(0:length(sOFDM)-1)*dt;
% plot(t,sOFDM);
% title('Signal CP-OFDM');
% xlabel('Time [s]');
% ylabel('Amplitude');
 
 
fftOFDM = fft(sOFDM);
fftOFDM = fftshift(fftOFDM);
freq = (-length(sOFDM)/2:length(sOFDM)/2-1)*fBase;
 
 
 
% figure(2);
% plot(freq, 2*abs(fftOFDM)/Fs);
% title('Spectrum of sine');
% xlabel('Frequency [Hz]');
% ylabel('Amplitude');
%  
 
% figure(3);
  pOFDM = sOFDM.^2;
% plot(t, 10*log10(pOFDM));
% title('Power of CP-OFDM signal');
% xlabel('Time [s]');
% ylabel('Power [dB]');
 
 
powerOFDM = 0;
for k= 1: length(pOFDM)
    powerOFDM = powerOFDM + pOFDM(k);
    
end
powerOFDM = powerOFDM/length(pOFDM);
snr_lin = 10^(5/10);    % 5dB
var = powerOFDM/snr_lin;
%var =2000;
noise = (var/sqrt(2))*(randn(1,length(sOFDM)) +i*randn(1,length(sOFDM)));
sOFDM_fft = fft(sOFDM) + noise*Fs/2;
%sOFDM = sOFDM + abs(noise);
sOFDM = ifft(sOFDM_fft);                  %add noise into signal
 
% figure(4);
% 
% plot(t,noise);
% title('Signal CP-OFDM with Gaussian noise');
% xlabel('Time [s]');
% ylabel('Amplitude');
 
 
sorted_noise = sort(abs(noise));
dx = 0:0.001:20;
count =1;
Fx = zeros(1,length(dx));
 
k=1;
while ( k<= length(sorted_noise))
    if count <length(dx)
        if sorted_noise(k)<=dx(count)
        Fx(count)= Fx(count) +1; 
        k = k+1;
        else 
            count = count +1;
            Fx(count) = Fx(count-1);
        end
    else
        Fx(count)= Fx(count) +1; 
        k=k+1;
    end
    
    
end
Fx = Fx./length(sorted_noise);
 
dx1 = 0:0.1:20;
Px = zeros(1,length(dx1));
Px(1) = Fx(100)/(dx(100));
for k = 2:length(dx1)-2
    Px(k) =(Fx(k*100)-Fx((k-1)*100))/(dx(k*100)-dx((k-1)*100));
end
 
 
figure(5);
subplot(2,1,1);
plot(dx,Fx);
title(' Cumulative distribution function');
xlabel('Value');
ylabel('F(x)');
 
subplot(2,1,2);
plot(dx1,Px);
title('Probability density function ');
xlabel('Value');
ylabel('P(x)');
 
 
 
%Send Signal
% fileID = fopen('OFDM_signal.txt','w');
% fprintf(fileID,'%d\n',fBase);
% fprintf(fileID,'%d\n',fFirst);
% fprintf(fileID,'%d\n',nChannel);
% fprintf(fileID,'%f\n',Tsig);
% 
% fprintf(fileID,'%f\n',sOFDM);
% fclose(fileID); 
 
 
 
 
 
signal = sOFDM;
sigSymbol = length(signal)/nSymbol;
lTg = sigSymbol-sigSymbol/(1+rTg);
 
 
 
 
for j = 1:nSymbol
   k = (j-1)*sigSymbol+1;
   sigOFDM(j).symbol=signal(k:k+sigSymbol-1); 
end
 
 
%cutting CP part
bitseq =[];
for k = 1:nSymbol
   sigOFDM(k).initSymbol=sigOFDM(k).symbol(lTg+1:length(sigOFDM(k).symbol));
   sigOFDM(k).fft = fft(sigOFDM(k).initSymbol).*2/Fs;
   for j=1:nChannel
       tBit(k,j).data = sigOFDM(k).fft(fFirst/fBase+j);
       tBit(k,j).bit =decoding16QAM(tBit(k,j).data,mapQAM);
       bitseq = [bitseq tBit(k,j).bit];
    end
end
 
 
figure(1);
plot16QAM(mapQAM);
hold on;
for k = 1:nSymbol
   for j=1:nChannel
   rBit = real(tBit(k,j).data);
   iBit = -imag(tBit(k,j).data);
   plot(iBit,rBit,'r*');
   hold on;
   end
end
 A125

4.完整MATLAB

V

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/97547.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

非科班出身零基础能学好编程吗

非科班出身零基础能学好编程吗

近几年IT行业越来越火热&#xff0c;有很多人想转行跨界进入这个行业&#xff0c;那么作为初学者的你&#xff0c;是不是也很困惑&#xff0c;0基础非科班出身能学好编程吗&#xff1f; 编程是一个技术活&#xff0c;没有专业知识想进入这个行业是行不通的&#xff0c;这也决定…
阅读更多...
Go工程化项目布局

Go工程化项目布局

如果你尝试学习Go&#xff0c;或者你正在为自己建立一个Poc或者一个玩具项目&#xff0c;这个项目布局是没有啥必要的&#xff0c;从一些简单的事情开始&#xff08;一个main文件绰绰有余&#xff09;。当有更多的人参与这个项目的时候&#xff0c;你讲需要更多的结构&#xff…
阅读更多...
基于springboot超市进销存管理系统（Java毕业设计，包含部署文档）

基于springboot超市进销存管理系统（Java毕业设计，包含部署文档）

大家好✌&#xff01;我是CZ淡陌。一名专注以理论为基础实战为主的技术博主&#xff0c;将再这里为大家分享优质的实战项目&#xff0c;本人在Java毕业设计领域有多年的经验&#xff0c;陆续会更新更多优质的Java实战项目&#xff0c;希望你能有所收获&#xff0c;少走一些弯路…
阅读更多...
神经网络种类及应用领域,常用的神经网络有哪些

神经网络种类及应用领域,常用的神经网络有哪些

1、神经网络算法的三大类分别是&#xff1f; 神经网络算法的三大类分别是&#xff1a; 1、前馈神经网络&#xff1a; 这是实际应用中最常见的神经网络类型。第一层是输入&#xff0c;最后一层是输出。如果有多个隐藏层&#xff0c;我们称之为“深度”神经网络。他们计算出一…
阅读更多...
[附源码]Python计算机毕业设计Django网上鲜花购物系统

[附源码]Python计算机毕业设计Django网上鲜花购物系统

项目运行 环境配置&#xff1a; Pychram社区版 python3.7.7 Mysql5.7 HBuilderXlist pipNavicat11Djangonodejs。 项目技术&#xff1a; django python Vue 等等组成&#xff0c;B/S模式 pychram管理等等。 环境需要 1.运行环境&#xff1a;最好是python3.7.7&#xff0c;…
阅读更多...
一篇文章带你轻松手撕AVL树的构建

一篇文章带你轻松手撕AVL树的构建

1.AVL树介绍 我们知道一般情况下二叉搜索树的查找效率是很高的&#xff0c;但是遇到极端情况下时间复杂度就会来到O(N) 那么为了消除这种极端情况的影响&#xff0c;我们就需要调节这个二叉树通过一些操作转成一颗二叉平衡树&#xff0c;调节完毕就会得到一颗AVL树。 2.AVL树模…
阅读更多...
【Linux】第二部分 保姆级手把手教你如何安装Linux

【Linux】第二部分 保姆级手把手教你如何安装Linux

【Linux】第二部分 保姆级手把手教你如何安装Linux 文章目录【Linux】第二部分 保姆级手把手教你如何安装Linux2.保姆级手把手教你如何安装Linux首先下载vmware接下来下载centOS**接着开启虚拟机,对操作系统进行配置**总结2.保姆级手把手教你如何安装Linux 首先下载vmware vm…
阅读更多...
阿里云服务器安装oracle11g

阿里云服务器安装oracle11g

1.服务器配置 //linux版本 CentOS-7-x86_64 //oracle版本 linux.x64_11gR2 //查看服务器的CPU个数 cat /proc/cpuinfo | grep physical | sort -n | uniq | wc -l //查看服务器的型号 dmidecode -s system-product-name //查看服务器的cpu型号…
阅读更多...
LeetCode题解 14 (3,98) 无重复字符的最长子串,验证二叉搜索树

LeetCode题解 14 (3,98) 无重复字符的最长子串,验证二叉搜索树

文章目录无重复字符的最长子串(3)代码解答&#xff1a;验证二叉搜索树(98)代码解答&#xff1a;无重复字符的最长子串(3) 从题目中可以得知我们要找到该字符串中没有重复元素的最长字串,这道题可以采用滑动窗口的方法来解决,今天在这里我们采用新的方法来解决。 首先我们先将该…
阅读更多...
转行学Python开发 怎么快速入门

转行学Python开发 怎么快速入门

对于很多转行的新手而言&#xff0c;直接参加培训班是最省时省力的事情&#xff0c;参加培训班既不用担心自己学不会&#xff0c;也不用担心遇到不懂的问题时没有人解答&#xff0c;更重要的是培训班理论实践的教学更贴合实际市场需求。 Python目前是IT行业需求量最大的语言&a…
阅读更多...
能够让你装逼的10个Python小技巧

能够让你装逼的10个Python小技巧

列表推导式 你有一个list&#xff1a; bag [1, 2, 3, 4, 5] 现在你想让所有元素翻倍&#xff0c;让它看起来是这个样子&#xff1a; [2, 4, 6, 8, 10] 大多初学者&#xff0c;根据之前语言的经验会大概这样来做 bag [1, 2, 3, 4, 5] for i in range(len(bag)): bag[i] ba…
阅读更多...
GitHub要求所有用户在2023年底前启用双因素身份验证

GitHub要求所有用户在2023年底前启用双因素身份验证

©网络研究院 GitHub 将要求所有在平台上贡献代码的用户在 2023 年底之前启用双因素身份验证 (2FA) 作为对其帐户的额外保护措施。 双因素身份验证通过在需要输入一次性代码的登录过程中引入额外步骤来提高帐户的安全性。 对于 GitHub 用户来说&#xff0c;账户接管可能…
阅读更多...
猿如意中的【Wireshark】网络包分析工具详情介绍

猿如意中的【Wireshark】网络包分析工具详情介绍

一、工具名称 Wireshark-win64-3.6.5 二、下载安装渠道 Wireshark-win64-3.6.5 通过CSDN官方开发的【猿如意】客户端进行下载安装。 对&#xff0c;你没有看错&#xff0c;就是来自CSDN官方&#xff0c;这次&#xff0c;CSDN果然没有辜负广大技术人的期望&#xff0c;现在…
阅读更多...
Redis详解

Redis详解

Redis详解1. 概述1.1 互联网架构的演变历程1.2 Redis入门介绍1.3 Redis/Memcache/MongoDB对比1.3.1 Redis和Memcache1.3.2 Redis和MongoDB1.4 分布式数据库CAP原理1.4.1 CAP简介1.4.2 CAP理论1.4.3 CAP总结2. 下载与安装2.1 下载2.2 安装2.3 安装后的操作2.3.1 后台运行方式2.3…
阅读更多...
高级网络应用复习——三层生成树速端口实验（带命令，保姆级）

高级网络应用复习——三层生成树速端口实验（带命令，保姆级）

作者简介&#xff1a;一名在校云计算网络运维学生、每天分享网络运维的学习经验、和学习笔记。 座右铭&#xff1a;低头赶路&#xff0c;敬事如仪 个人主页&#xff1a;网络豆的主页​​​​​​ 目录 前言 一.知识点总结 1.生成树STP 2.生成树的算法 3.人为配置的作用…
阅读更多...
罗德里格旋转公式 (Rodrigues’ Rotation Formula)

罗德里格旋转公式 (Rodrigues’ Rotation Formula)

关于三维空间中的旋转&#xff0c;我们以前提到过基于欧拉角的旋转表达矩阵&#xff0c;它们分别描述了围绕 x 轴、y 轴、z 轴旋转后坐标应当如何变化。事实上&#xff0c;我们可以更进一步&#xff0c;推导出一个通用的、围绕过原点的任意轴旋转的公式。 题设 这一节我们来描…
阅读更多...
linux-网络-nc命令

linux-网络-nc命令

目录 概述 nc命令常用参数 nc命令示例 实现TCP/UDP侦听 作为client端发起TCP/UDP连接 服务器之间传输文件 网络测速 概述 在centos中&#xff0c;nc命令是ncat的软链接。 ncat是一个功能丰富的网络实用程序&#xff0c;是为nmap项目编写的&#xff08;Network Mapper&…
阅读更多...
12个python超强学习网站！

12个python超强学习网站！

一、python学习网站 1 CSDN 特点&#xff1a;从免费视频到入门项目&#xff0c;从入门到进阶&#xff0c;学习视频应有尽有&#xff0c;还有Python学习社区&#xff0c;良好的学习和沟通氛围&#xff01; 2 Python123 地址&#xff1a;python123 特点&#xff1a;北京理工…
阅读更多...
适合零基础人群学习的Python入门教程，快来学习吧

适合零基础人群学习的Python入门教程，快来学习吧

适合零基础人群学习的Python入门教程学什么&#xff1f;小编为大家准备的Python学习教程&#xff0c;课程主要讲解&#xff1a;Python核心编程、Linux基础、前端开发、Web开发、爬虫开发、人工智能等内容。 对于初学者想更轻松的学好Python开发&#xff0c;爬虫技术&#xff0c…
阅读更多...
个人博客 HTML个人介绍网页 学生个人网页设计作品 学生个人网页模板 简单个人主页成品 个人网页制作 HTML学生个人网站作业设计

个人博客 HTML个人介绍网页 学生个人网页设计作品 学生个人网页模板 简单个人主页成品 个人网页制作 HTML学生个人网站作业设计

&#x1f389;精彩专栏推荐 &#x1f4ad;文末获取联系 ✍️ 作者简介: 一个热爱把逻辑思维转变为代码的技术博主 &#x1f482; 作者主页: 【主页——&#x1f680;获取更多优质源码】 &#x1f393; web前端期末大作业&#xff1a; 【&#x1f4da;毕设项目精品实战案例 (10…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023