关于三维空间中的旋转,我们以前提到过基于欧拉角的旋转表达矩阵,它们分别描述了围绕 x 轴、y 轴、z 轴旋转后坐标应当如何变化。事实上,我们可以更进一步,推导出一个通用的、围绕过原点的任意轴旋转的公式。
题设
这一节我们来描述我们已知的条件和待求的目标:
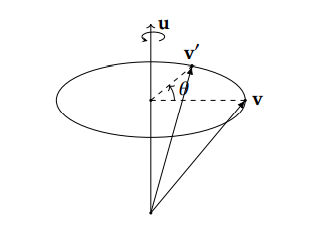
给定一个方向向量 u ⃗ \vec{u} u作为旋转轴, v ⃗ \vec{v} v为待旋转的向量,我们希望得到 v ⃗ \vec{v} v围绕着 u ⃗ \vec{u} u逆时针旋转 θ \theta θ角度之后的向量 v ′ ⃗ \vec{v'} v′。注意, v ′ ⃗ \vec{v'} v′的表达式必须用已知条件 u ⃗ \vec{u} u、 v ⃗ \vec{v} v和 θ \theta θ来表达。
思路
旋转前后向量的长度不会变化,反而是如何计算旋转后向量的方向成为了一个难题。我们采用分解向量的思路来解决向量旋转的问题——把 v ⃗ \vec{v} v分解为平行于 u ⃗ \vec{u} u的向量 v / / ⃗ \vec{v_{//}} v//和垂直于 u ⃗ \vec{u} u的向量 v ⊥ ⃗ \vec{v_\bot} v⊥,分解的示意图如下:
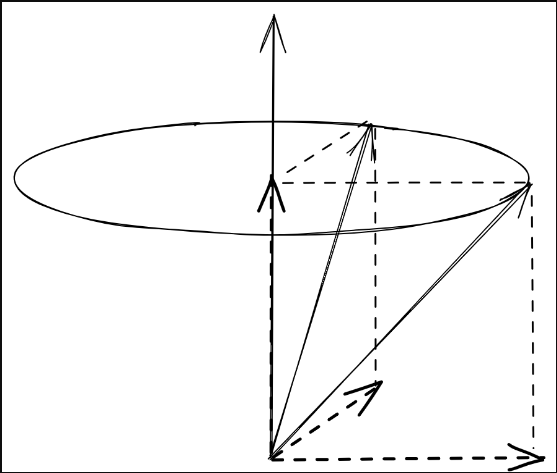
这样定义向量的分解方式是有好处的,我们可以发现,旋转前后 v / / ⃗ \vec{v_{//}} v//没有变化,而旋转前的 v ⊥ ⃗ \vec{v_\bot} v⊥、旋转后的 v ⊥ ′ ⃗ \vec{v'_\bot} v⊥′都在一个平面内,同一个平面内的旋转比起三维旋转要好解决的多。
公式推导
v
/
/
⃗
\vec{v_{//}}
v//实际上是
v
⃗
\vec{v}
v在
u
⃗
\vec{u}
u上的正交投影,因此我们可以得出:
KaTeX parse error: Expected 'EOF', got '&' at position 14: \vec{v_{//}}&̲=|\vec{v}|\frac…
然后,我们运用向量减法给出
v
⊥
⃗
\vec{v_{\bot}}
v⊥的表达式:
v
⊥
⃗
=
v
⃗
−
v
/
/
⃗
\vec{v_{\bot}}=\vec{v}-\vec{v_{//}}
v⊥=v−v//
接下来,我们需要给出
v
⊥
′
⃗
\vec{v'_\bot}
v⊥′的表达式。给出一个直观的旋转俯视图:
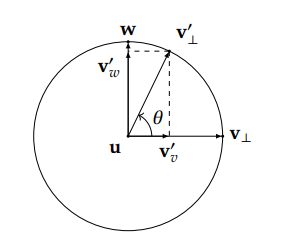
先定义 w ⃗ \vec{w} w。引入这个向量是为了正交分解 v ⊥ ′ ⃗ \vec{v'_\bot} v⊥′,因此它必须垂直于 v ⊥ ⃗ \vec{v_{\bot}} v⊥。如果你对叉乘很熟悉的话,很快就能想到我们可以用 u ⃗ × v ⃗ \vec{u}\times\vec{v} u×v来得到具有这样的性质的向量。注意叉乘的顺序,根据旋转示意图和右手定则, u ⃗ × v ⊥ ⃗ \vec{u}\times\vec{v_{\bot}} u×v⊥的向量方向才是俯视图中的 w ⃗ \vec{w} w方向。
然后,我们把
v
⊥
′
⃗
\vec{v'_\bot}
v⊥′正交分解成平行于
v
⊥
⃗
\vec{v_{\bot}}
v⊥的
v
v
′
⃗
\vec{v'_{v}}
vv′和平行于
w
⃗
\vec{w}
w的
v
w
′
⃗
\vec{v'_w}
vw′,并给出
v
⊥
′
⃗
\vec{v'_\bot}
v⊥′的表达式。
v
⊥
′
⃗
=
v
v
′
⃗
+
v
w
′
⃗
v
v
′
⃗
=
∣
v
⊥
⃗
∣
cos
θ
⋅
v
⊥
⃗
∣
v
⊥
⃗
∣
=
v
⊥
⃗
cos
θ
v
w
′
⃗
=
∣
v
⊥
⃗
∣
sin
θ
⋅
u
⃗
×
v
⊥
⃗
∣
u
⃗
×
v
⊥
⃗
∣
∣
u
⃗
×
v
⊥
⃗
∣
=
∣
u
⃗
∣
∣
v
⊥
⃗
∣
sin
(
π
/
2
)
=
∣
v
⊥
⃗
∣
v
w
′
⃗
=
(
u
⃗
×
v
⊥
⃗
)
sin
θ
v
⊥
′
⃗
=
v
⊥
⃗
cos
θ
+
(
u
⃗
×
v
⊥
⃗
)
sin
θ
\vec{v'_\bot}=\vec{v'_{v}}+\vec{v'_w}\\ \vec{v'_{v}}=|\vec{v_\bot}|\cos\theta\cdot\frac{\vec{v_\bot}}{|\vec{v_\bot}|}=\vec{v_\bot}\cos\theta\\ \vec{v'_w}=|\vec{v_\bot}|\sin\theta\cdot\frac{\vec{u}\times\vec{v_{\bot}}}{|\vec{u}\times\vec{v_{\bot}}|}\\ |\vec{u}\times\vec{v_{\bot}}|=|\vec{u}||\vec{v_{\bot}}|\sin(\pi/2)=|\vec{v_{\bot}}|\\ \vec{v'_w}=(\vec{u}\times\vec{v_{\bot}})\sin\theta\\ \vec{v'_\bot}=\vec{v_\bot}\cos\theta+(\vec{u}\times\vec{v_{\bot}})\sin\theta
v⊥′=vv′+vw′vv′=∣v⊥∣cosθ⋅∣v⊥∣v⊥=v⊥cosθvw′=∣v⊥∣sinθ⋅∣u×v⊥∣u×v⊥∣u×v⊥∣=∣u∣∣v⊥∣sin(π/2)=∣v⊥∣vw′=(u×v⊥)sinθv⊥′=v⊥cosθ+(u×v⊥)sinθ
上面的式子可以进一步被化简,我们代入
v
⊥
⃗
\vec{v_{\bot}}
v⊥的表达式,并运用叉乘的分配律:
v
⊥
′
⃗
=
(
v
⃗
−
v
/
/
⃗
)
cos
θ
+
(
u
⃗
×
(
v
⃗
−
v
/
/
⃗
)
)
sin
θ
使用分配律,
(
u
⃗
×
(
v
⃗
−
v
/
/
⃗
)
)
=
u
⃗
×
v
⃗
−
u
⃗
×
v
/
/
⃗
因为共线,
u
⃗
×
v
/
/
⃗
=
0
v
⊥
′
⃗
=
v
⃗
cos
θ
−
v
/
/
⃗
cos
θ
+
(
u
⃗
×
v
⃗
)
sin
θ
\vec{v'_\bot}=(\vec{v}-\vec{v_{//}})\cos\theta+(\vec{u}\times(\vec{v}-\vec{v_{//}}))\sin\theta\\ 使用分配律,(\vec{u}\times(\vec{v}-\vec{v_{//}}))=\vec{u}\times\vec{v}-\vec{u}\times\vec{v_{//}}\\ 因为共线,\vec{u}\times\vec{v_{//}}=0\\ \vec{v'_\bot}=\vec{v}\cos\theta-\vec{v_{//}}\cos\theta+(\vec{u}\times\vec{v})\sin\theta
v⊥′=(v−v//)cosθ+(u×(v−v//))sinθ使用分配律,(u×(v−v//))=u×v−u×v//因为共线,u×v//=0v⊥′=vcosθ−v//cosθ+(u×v)sinθ
最后,我们终于可以给出
v
′
⃗
\vec{v'}
v′的表达式:
v
′
⃗
=
v
/
/
⃗
+
v
⊥
′
⃗
v
′
⃗
=
v
/
/
⃗
+
v
⃗
cos
θ
−
v
/
/
⃗
cos
θ
+
(
u
⃗
×
v
⃗
)
sin
θ
=
v
⃗
cos
θ
+
(
1
−
cos
θ
)
v
/
/
⃗
+
(
u
⃗
×
v
⃗
)
sin
θ
v
′
⃗
=
v
⃗
cos
θ
+
(
1
−
cos
θ
)
(
u
⃗
⋅
v
⃗
)
u
⃗
+
(
u
⃗
×
v
⃗
)
sin
θ
\vec{v'}=\vec{v_{//}}+\vec{v'_{\bot}}\\ \vec{v'}=\vec{v_{//}}+\vec{v}\cos\theta-\vec{v_{//}}\cos\theta+(\vec{u}\times\vec{v})\sin\theta=\vec{v}\cos\theta+(1-\cos\theta)\vec{v_{//}}+(\vec{u}\times\vec{v})\sin\theta\\ \vec{v'}=\vec{v}\cos\theta+(1-\cos\theta)(\vec{u}\cdot{\vec{v}})\vec{u}+(\vec{u}\times\vec{v})\sin\theta
v′=v//+v⊥′v′=v//+vcosθ−v//cosθ+(u×v)sinθ=vcosθ+(1−cosθ)v//+(u×v)sinθv′=vcosθ+(1−cosθ)(u⋅v)u+(u×v)sinθ
上式的结果即是作为标题而提及的 Rodrigues’ Rotation Formula。
化简为矩阵
我们需要进一步化简公式,得到其等价的矩阵表达形式,才方便代码的实现。
首先,我们需要知道向量三重积公式:
a
⃗
×
(
b
⃗
×
c
⃗
)
=
(
a
⃗
⋅
c
⃗
)
⋅
b
⃗
−
(
a
⃗
⋅
b
⃗
)
⋅
c
⃗
\vec{a}\times(\vec{b}\times\vec{c})=(\vec{a}\cdot\vec{c})\cdot\vec{b}-(\vec{a}\cdot\vec{b})\cdot\vec{c}
a×(b×c)=(a⋅c)⋅b−(a⋅b)⋅c
然后,我们还需要知道,向量的叉乘与矩阵之间的联系:
a
⃗
×
b
⃗
=
(
y
a
z
b
−
z
a
y
b
z
a
x
b
−
x
a
z
b
x
a
y
b
−
y
a
x
b
)
=
A
⋅
b
=
(
0
−
z
a
y
a
z
a
0
−
x
a
−
y
a
x
a
0
)
(
x
b
y
b
z
b
)
\vec{a}\times\vec{b}=\begin{pmatrix}y_az_b-z_ay_b\\z_ax_b-x_az_b\\x_ay_b-y_ax_b\end{pmatrix}=A\cdot b= \begin{pmatrix} 0 & -z_a & y_a\\ z_a& 0 & -x_a\\ -y_a& x_a & 0 \end{pmatrix}\begin{pmatrix}x_b\\y_b\\z_b\end{pmatrix}
a×b=
yazb−zaybzaxb−xazbxayb−yaxb
=A⋅b=
0za−ya−za0xaya−xa0
xbybzb
向量的叉乘可以化为矩阵与向量的乘积,而且需要注意的是,矩阵只与左边的向量有关。
我们化简的目标是得到下述形式的表达式,其中M是矩阵。
v
′
⃗
=
M
⋅
v
⃗
\vec{v'}=M\cdot\vec{v}
v′=M⋅v
再次观察公式:
v
′
⃗
=
v
⃗
cos
θ
+
(
1
−
cos
θ
)
(
u
⃗
⋅
v
⃗
)
u
⃗
+
(
u
⃗
×
v
⃗
)
sin
θ
\vec{v'}=\vec{v}\cos\theta+(1-\cos\theta)(\vec{u}\cdot{\vec{v}})\vec{u}+(\vec{u}\times\vec{v})\sin\theta
v′=vcosθ+(1−cosθ)(u⋅v)u+(u×v)sinθ
第一项和第三项都可以快速给出等价的矩阵形式,其中,
v
⃗
cos
θ
\vec{v}\cos\theta
vcosθ可以化为:
v
⃗
cos
θ
=
(
cos
θ
0
0
0
cos
θ
0
0
0
cos
θ
)
⋅
v
⃗
\vec{v}\cos\theta=\begin{pmatrix} \cos\theta & 0 & 0\\ 0 & \cos\theta & 0\\ 0 & 0 & \cos\theta \end{pmatrix}\cdot\vec{v}
vcosθ=
cosθ000cosθ000cosθ
⋅v
正如前文所说,
(
u
⃗
×
v
⃗
)
sin
θ
(\vec{u}\times\vec{v})\sin\theta
(u×v)sinθ也可以化成矩阵乘向量的形式,这里记向量
u
⃗
\vec{u}
u形成的矩阵为
R
u
R_u
Ru,可以得到
(
u
⃗
×
v
⃗
)
sin
θ
=
R
u
sin
θ
⋅
v
⃗
(\vec{u}\times\vec{v})\sin\theta=R_u\sin\theta\cdot\vec{v}
(u×v)sinθ=Rusinθ⋅v
比较难以化简的是第二项,处于外部的是向量
u
⃗
\vec{u}
u而不是
v
⃗
\vec{v}
v,这给我们带来了一些麻烦。观察
(
u
⃗
⋅
v
⃗
)
u
⃗
(\vec{u}\cdot{\vec{v}})\vec{u}
(u⋅v)u这一项和已知的三重积公式,或许可以想办法配凑另外一项,从而把点乘变为叉乘,再运用叉乘的性质化作矩阵。有好几种可能的叉乘式,最终我们选择配凑出这样的叉乘:
u
⃗
×
(
u
⃗
×
v
⃗
)
\vec{u}\times(\vec{u}\times\vec{v})
u×(u×v)。其中一个理由是
u
⃗
\vec{u}
u都在左边,我们可以复用前面提到的矩阵
R
u
R_u
Ru;另一个理由是缺失的那一项很好配凑:
u
⃗
×
(
u
⃗
×
v
⃗
)
=
(
u
⃗
⋅
v
⃗
)
u
⃗
−
(
u
⃗
⋅
u
⃗
)
v
⃗
=
(
u
⃗
⋅
v
⃗
)
u
⃗
−
v
⃗
\vec{u}\times(\vec{u}\times\vec{v})=(\vec{u}\cdot\vec{v})\vec{u}-(\vec{u}\cdot\vec{u})\vec{v}=(\vec{u}\cdot\vec{v})\vec{u}-\vec{v}
u×(u×v)=(u⋅v)u−(u⋅u)v=(u⋅v)u−v
明确了目标之后,开始化简:
v
⃗
cos
θ
+
(
1
−
cos
θ
)
(
u
⃗
⋅
v
⃗
)
u
⃗
=
v
⃗
cos
θ
+
v
⃗
−
v
⃗
=
v
⃗
−
(
1
−
cos
θ
)
v
⃗
+
(
1
−
cos
θ
)
(
u
⃗
⋅
v
⃗
)
u
⃗
=
v
⃗
+
(
1
−
cos
θ
)
(
(
u
⃗
⋅
v
⃗
)
u
⃗
−
v
⃗
)
=
v
⃗
+
(
1
−
cos
θ
)
(
u
⃗
×
(
u
⃗
×
v
⃗
)
)
\vec{v}\cos\theta+(1-\cos\theta)(\vec{u}\cdot{\vec{v}})\vec{u}=\vec{v}\cos\theta+\vec{v}-\vec{v}=\vec{v}-(1-\cos\theta)\vec{v}+(1-\cos\theta)(\vec{u}\cdot{\vec{v}})\vec{u}\\ =\vec{v}+(1-\cos\theta)((\vec{u}\cdot{\vec{v}})\vec{u}-\vec{v})\\ =\vec{v}+(1-\cos\theta)(\vec{u}\times(\vec{u}\times\vec{v}))
vcosθ+(1−cosθ)(u⋅v)u=vcosθ+v−v=v−(1−cosθ)v+(1−cosθ)(u⋅v)u=v+(1−cosθ)((u⋅v)u−v)=v+(1−cosθ)(u×(u×v))
我们再次利用叉乘转换为矩阵的性质,可以得到:
u
⃗
×
(
u
⃗
×
v
⃗
)
=
u
⃗
×
(
R
u
⋅
v
⃗
)
=
R
u
2
⋅
v
⃗
\vec{u}\times(\vec{u}\times\vec{v})=\vec{u}\times(R_u\cdot\vec{v})=R_u^2\cdot\vec{v}
u×(u×v)=u×(Ru⋅v)=Ru2⋅v
最后我们得到了一个比较复杂的矩阵:
v
′
⃗
=
v
⃗
+
(
1
−
cos
θ
)
⋅
R
u
2
⋅
v
⃗
+
R
u
sin
θ
⋅
v
⃗
记
I
为单位矩阵
v
′
⃗
=
(
I
+
(
1
−
cos
θ
)
⋅
R
u
2
+
R
u
sin
θ
)
⋅
v
⃗
M
=
I
+
(
1
−
cos
θ
)
⋅
R
u
2
+
R
u
sin
θ
\vec{v'}=\vec{v}+(1-\cos\theta)\cdot R_u^2\cdot\vec{v}+R_u\sin\theta\cdot\vec{v}\\ 记I为单位矩阵\\ \vec{v'}=(I+(1-\cos\theta)\cdot R_u^2+R_u\sin\theta)\cdot\vec{v}\\ M=I+(1-\cos\theta)\cdot R_u^2+R_u\sin\theta
v′=v+(1−cosθ)⋅Ru2⋅v+Rusinθ⋅v记I为单位矩阵v′=(I+(1−cosθ)⋅Ru2+Rusinθ)⋅vM=I+(1−cosθ)⋅Ru2+Rusinθ
M即为我们所求的矩阵。
Refer
罗德里格旋转公式(Rodrigues’ rotation formula)
四元数与三维旋转










![kali 安装AWVS [赠附件]](https://img-blog.csdnimg.cn/img_convert/295aba7090e9806b6b5e1fc61daf4e58.png)