无重复字符的最长子串(3)

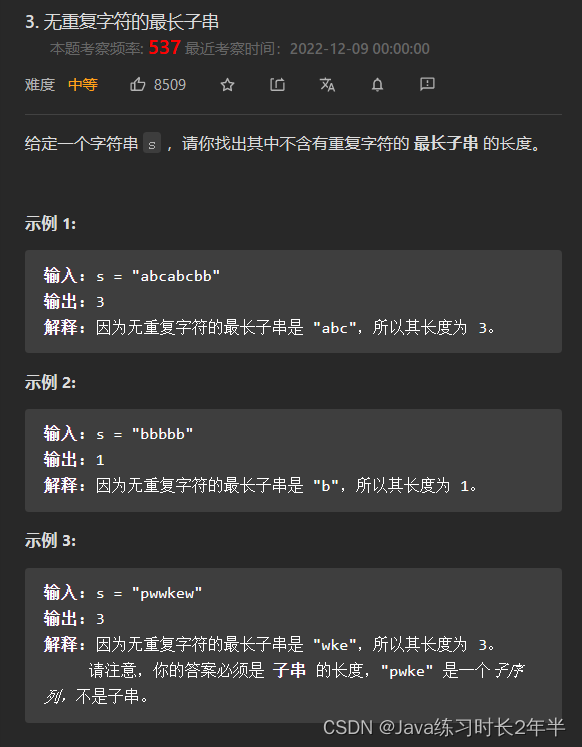
从题目中可以得知我们要找到该字符串中没有重复元素的最长字串,这道题可以采用滑动窗口的方法来解决,今天在这里我们采用新的方法来解决。

首先我们先将该字符串转变为字符数组,同时创建1个HashSet,(因为HashSet是不允许存放相同元素的)定义1个新的指针index来准备遍历

        HashSet<Character> characters = new HashSet<>();
        char[] chars = s.toCharArray();
        int index = 0;

我们还要定义1个字符串最大的长度max,和一个start开始值（当一个重复元素加不进去时,我们就需要从头开始进行删除元素,直到能加入元素位置）

   int start = 0;
   int max = 0;

这时我们就开始进行遍历数组,往Hashet里面加入元素,如果可以加入,我们就更新max的值,不可以加入我们就用到start来从头开始删除元素,直到该元素可以加入为止。

         while(index < chars.length){
            //先往里面加元素
            char aChar = chars[index];
            //如果能加进去就直接添加
            if(characters.add(aChar)){
                max = Math.max(max,characters.size());
                index++;
            }else{
                //如果不能加进去,就从头部开始移除元素,直到能加进去为止
                characters.remove(chars[start]);
                start++;
            }
        }

代码解答：

class Solution {
    public int lengthOfLongestSubstring(String s) {
         //先定义1个HashSet
        HashSet<Character> characters = new HashSet<>();
        char[] chars = s.toCharArray();
        int index = 0;
        int start = 0;
        int max = 0;
        while(index < chars.length){
            //先往里面加元素
            char aChar = chars[index];
            //如果能加进去就直接添加
            if(characters.add(aChar)){
                max = Math.max(max,characters.size());
                index++;
            }else{
                //如果不能加进去,就从头部开始移除元素,直到能加进去为止
                characters.remove(chars[start]);
                start++;
            }
        }
        return max;
    }
}

验证二叉搜索树(98)

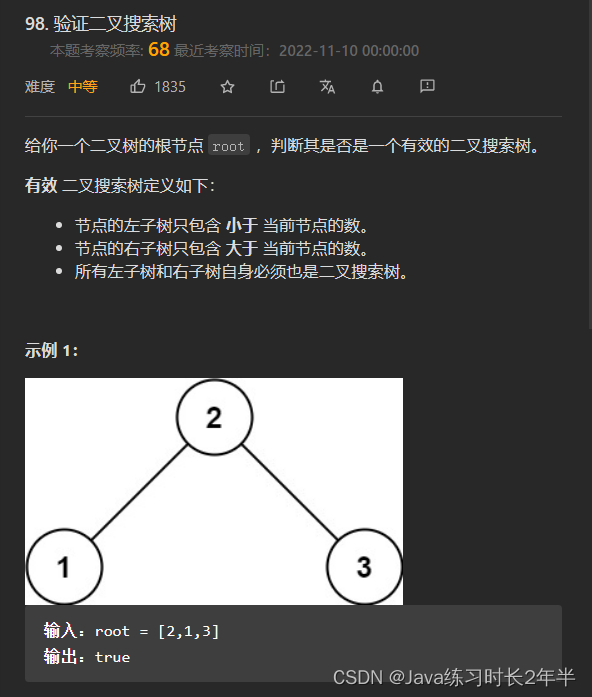
做这道题之前我们需要先知道什么是二叉搜索树,

二叉搜索树是根节点的数值要大于他的左子树的数值,同时也要小于右子树的数值,总结就是根节点的数值要比他的左子树的数值都要大,同时比右子树的数值都要小。

知道什么是二叉搜索树了,我们在这里就根据二叉搜索的特性来解决。
前面我们学习了二叉树的前序，中序，后序遍历,(学习二叉树的遍历)

这里我们将这个树进行一下中序遍历可以得到(1 2 3),可以看出是个升序数组,因此我们利用这一性质来进行做题

1.我们将该树进行中序遍历

//中序遍历
    public void infixOrder(TreeNode root){
        if(root == null){
            return;
        }
        infixOrder(root.left);
        list.add(root.val);
        infixOrder(root.right);
    }

这时我们就检查该数组是不是升序的，如果是升序的这个树就是二叉搜索树,如果不是就不是二叉搜索树,

        //判断该数组是不是升序的
        int min = list.get(0);
        for(int i = 1;i<list.size();i++){
            if(min < list.get(i)){
                //将min进行重置
                min = list.get(i);
            }else{
                return false;
            }
        }

代码解答：

class Solution {
    List<Integer> list = new ArrayList<>();
    public boolean isValidBST(TreeNode root) {
        //先将此树进行中序遍历
        infixOrder(root);
        //判断该数组是不是升序的
        int min = list.get(0);
        for(int i = 1;i<list.size();i++){
            if(min < list.get(i)){
                //将min进行重置
                min = list.get(i);
            }else{
                return false;
            }
        }
        return true;
    }
    //中序遍历
    public void infixOrder(TreeNode root){
        if(root == null){
            return;
        }
        infixOrder(root.left);
        list.add(root.val);
        infixOrder(root.right);
    }
}