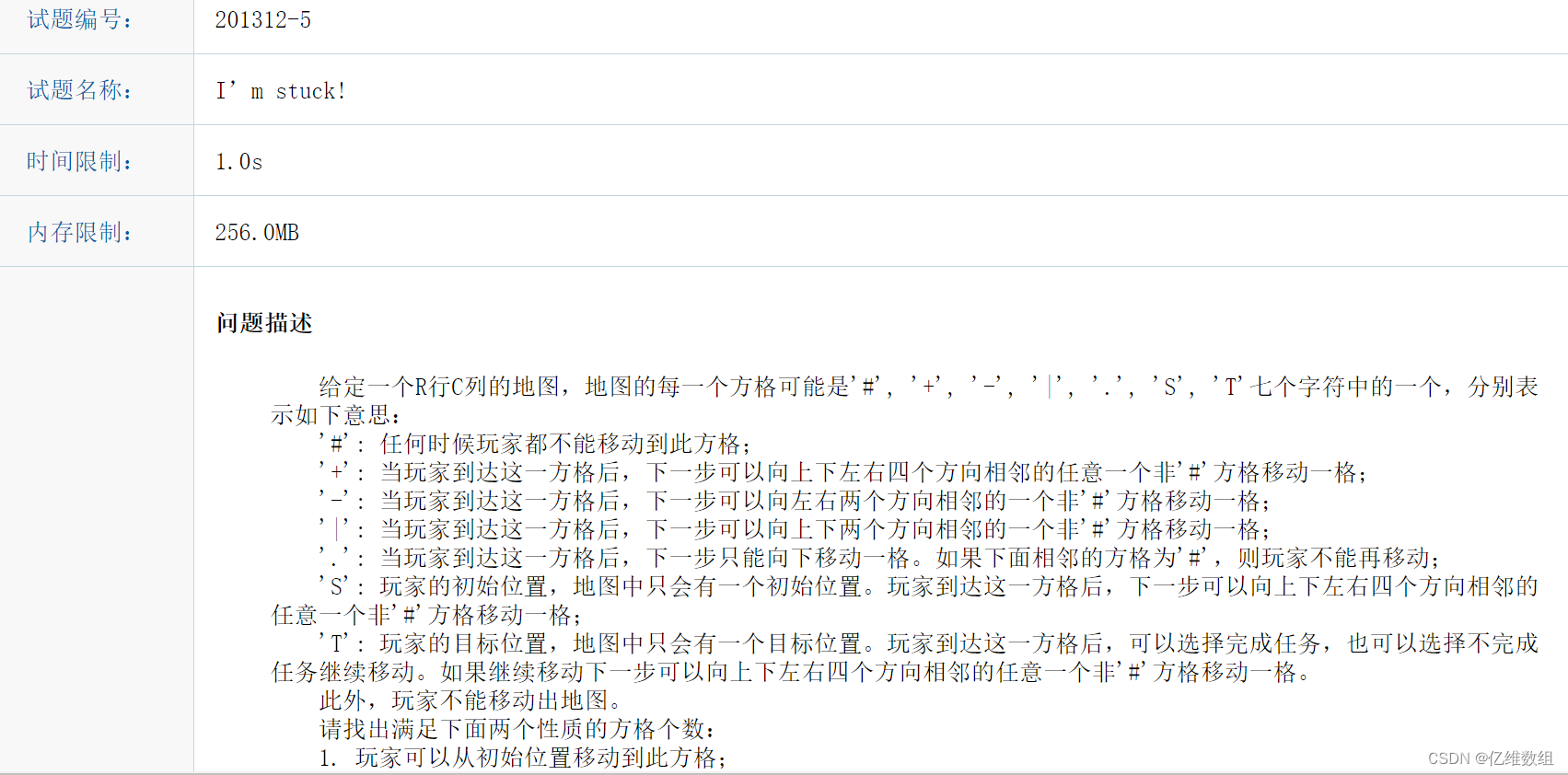
题目描述


思路讲解
总体步骤
第一步:从起点正向搜索,能到达的地方(x,y),给st1[x][y]标记为true
第二步:从终点反向搜索,能到达的地方(x,y),给st2[x][y]标记为true
第三步:设终点位置为(tx,ty),若st1[tx][ty]为false,输出“I'm stuck!”,否则,转第四步
第四步:统计所有满足st1[x][y]&&!st2[x][y]的点(x,y),其数量即为满足条件的点数
反向搜索与实现方式
从终点出发进行反向搜索的时候,如何判断可以不可以让某一个点的st2数组标记为true?
如下图所示:
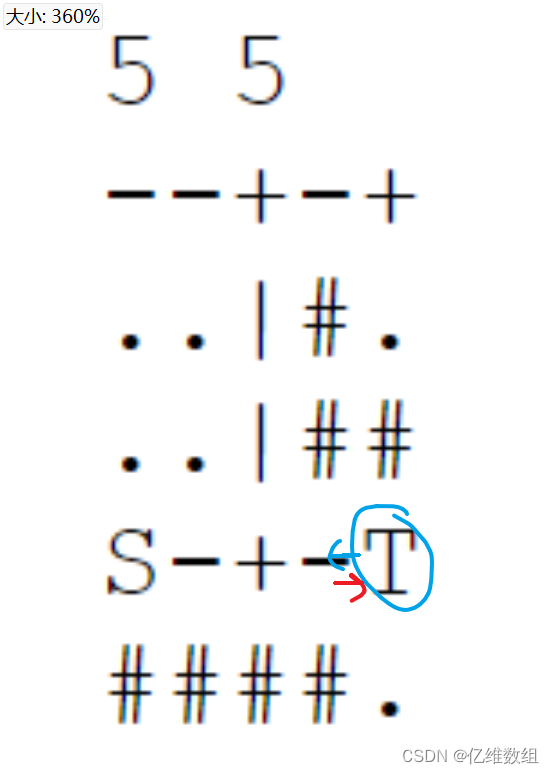
从终点查看反向是否能够到达左边的位置,其本质是看左边位置的点,能否顺着相反的方向到达终点!
那么如何表示这种相反的方向呢?
首先,利用我们常用的技巧,在开始设置方向数组dx和dy:
![]()
我们可以知道,下标为0代表上,下标为1代表右,下标为2代表下,下标为3代表左
所以当反向向左搜索时,我们要把代表左的“3”转换为代表右的“1”
同理当反向向右搜索时,我们要把代表右的“1”转换为代表左的“3”
同理当反向向上搜索时,我们要把代表上的“0”转换为代表下的“2”
同理当反向向下搜索时,我们要把代表下的“2”转换为代表上的“0”
如何实现这个转换?答案是:与2异或,即:
3^2=1 1^2=3 0^2=2 2^2=0
那么就可以得到反向搜索的dfs代码了:
 check函数的实现
check函数的实现
check函数用于判断从某一个点(a,b)出发,是否能沿方向k走一步,与上面相同,k=0代表向上,以此类推...
由题意,实现如下,非常容易理解

满分代码
#include<iostream>
using namespace std;
const int N=55;
char g[N][N];
bool st1[N][N],st2[N][N];
int dx[4]={-1,0,1,0},dy[4]={0,1,0,-1};
int n,m;
bool check(int a,int b,int k)
{
if(g[a][b]=='+'||g[a][b]=='S'||g[a][b]=='T')return true;
if(g[a][b]=='-'&&k%2==1)return true;
if(g[a][b]=='|'&&k%2==0)return true;
if(g[a][b]=='.'&&k==2)return true;
return false;
}
void dfs1(int x,int y)//从起点向其它点遍历
{
st1[x][y]=true;
for(int i=0;i<4;i++)
{
int ax=x+dx[i],ay=y+dy[i];
if(ax<0||ax>=n||ay<0||ay>=m||g[ax][ay]=='#'||st1[ax][ay])continue;
if(check(x,y,i))dfs1(ax,ay);
}
}
void dfs2(int x,int y)//从终点反向遍历至其它点
{
st2[x][y]=true;
for(int i=0;i<4;i++)
{
int ax=x+dx[i],ay=y+dy[i];
if(ax<0||ax>=n||ay<0||ay>=m||g[ax][ay]=='#'||st2[ax][ay])continue;
if(check(ax,ay,i^2))dfs2(ax,ay);
}
}
int main()
{
cin>>n>>m;
int tx,ty;
for(int i=0;i<n;i++)cin>>g[i];
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
{
if(g[i][j]=='S')dfs1(i,j);
else if(g[i][j]=='T')
{
tx=i,ty=j;
dfs2(tx,ty);
}
}
if(!st1[tx][ty])puts("I'm stuck!");
else
{
int res=0;
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
if(st1[i][j]&&!st2[i][j])res++;
cout<<res;
}
return 0;
}







![The WebSocket session [x] has been closed and no method (apart from close())](https://img-blog.csdnimg.cn/1f53af5b1f214d7c87b8ffa236d75483.png)