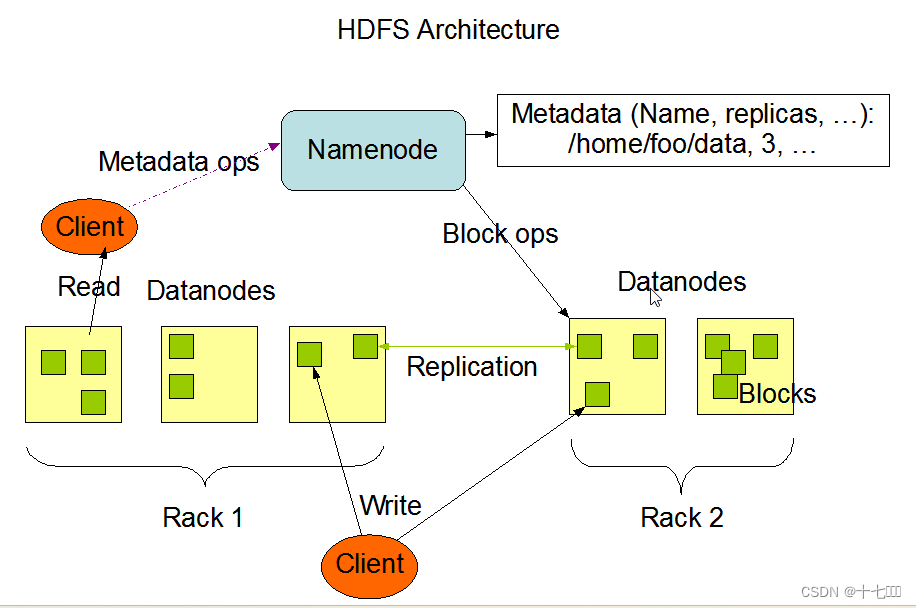
目录
一、插入排序
1、直接插入排序
1.1、排序方法
1.2、图解分析
1.3、代码实现
2、希尔排序
2.1、排序方法
2.2、图解分析
2.3、代码实现
二、选择排序
1、直接选择排序
1.1、排序方法
1.2、图解分析
1.3、代码实现
2、堆排序
2.1、排序方法
2.2、图解分析
2.3、代码实现
三、交换排序
1、冒泡排序
1.1、排序方法
1.2、图解分析
1.3、代码实现
2、快速排序
2.1、hoare排序
2.1.1、图解分析
2.1.2、代码实现
2.2、挖坑法
2.2.1、图解分析
2.2.2、代码实现
2.3、前后指针法
2.3.1、图解分析
2.3.2、代码实现
四、归并排序
1、排序方法
2、图解分析
3、代码实现
一、插入排序
基本思想:把待排序的数据按其关键码值的大小追个插入到一个有序序列中,得到一个新的有序序列。
1、直接插入排序
1.1、排序方法
当插入第i个元素时,数组的前i-1个元素已经有序,将第i个元素与前i-1个元素的关键码值进行比较,找到合适的位置插入,并将该位置之后的所有元素顺序后移即可。
1.2、图解分析
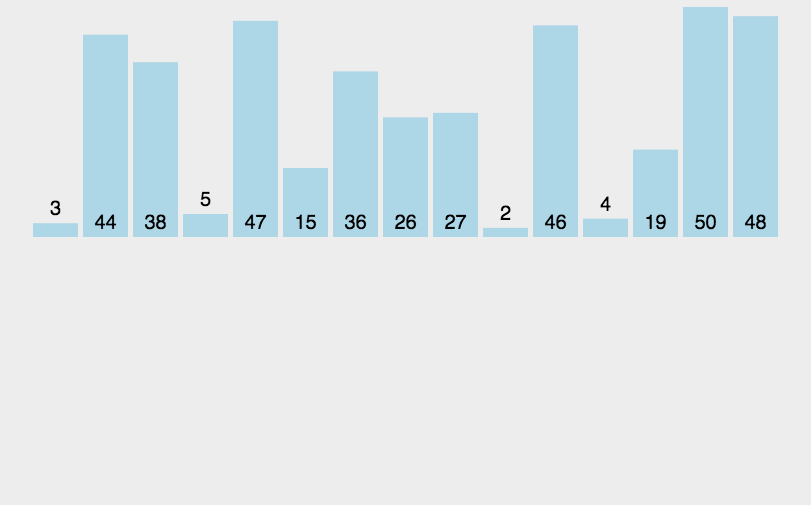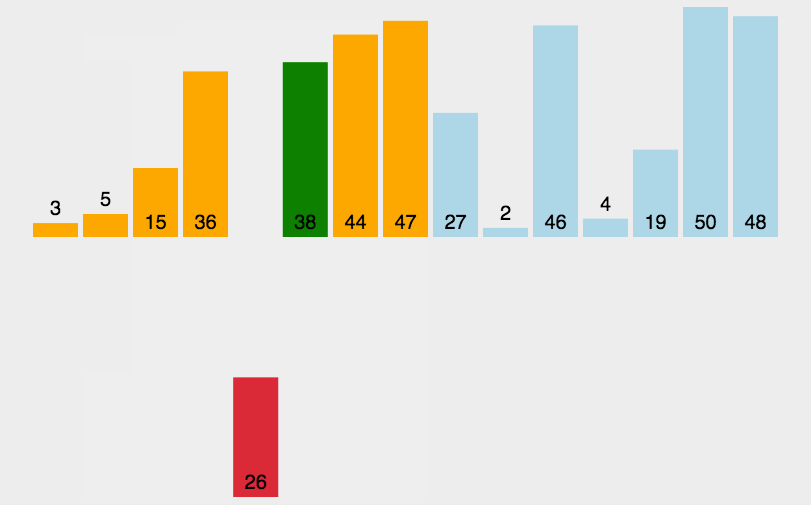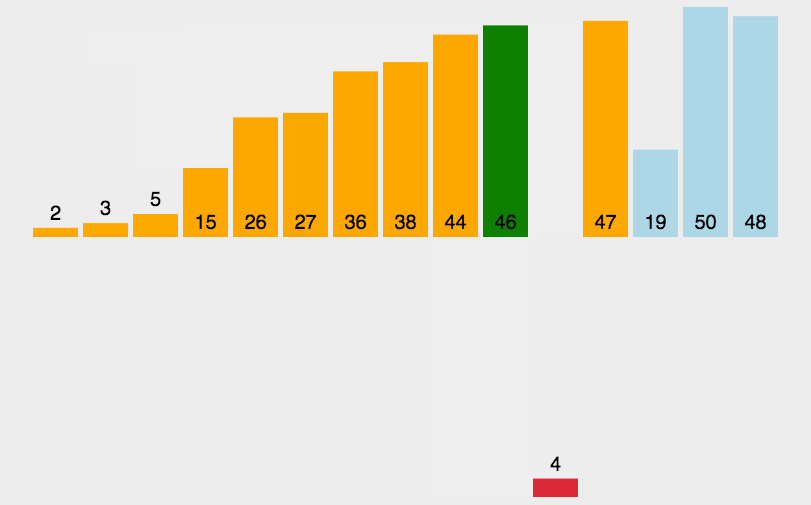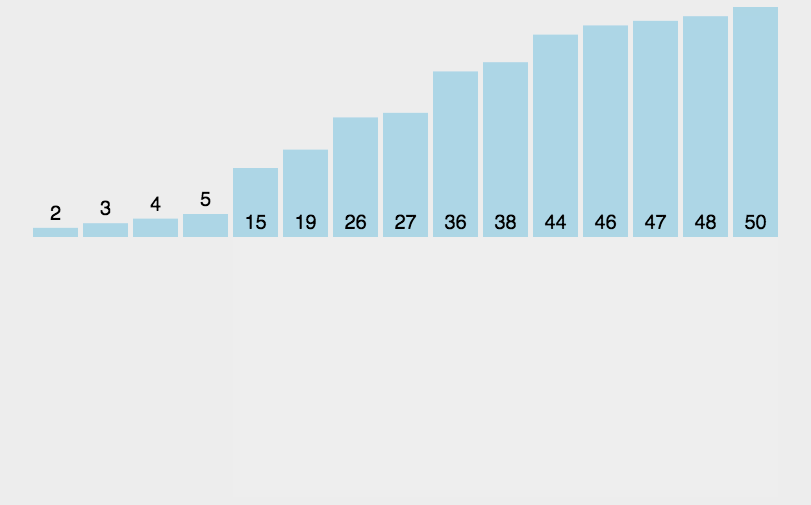
1.3、代码实现
// 直接插入排序
void InsertSort(int* a, int n)
{
for (int i = 0; i < n; i++)
{
int tmp = a[i];
int end = i-1;
while (end >= 0)
{
if (tmp < a[end])
{
a[end + 1] = a[end];
end--;
}
else
{
break;
}
}
a[end + 1] = tmp;;
}
}2、希尔排序
2.1、排序方法
希尔排序是对直接插入排序的优化。希尔排序的基本思想是:先选定一个合理的增量gap,把待排序文件中的数据分成gap个组,每一组中的相邻元素位置相差gap的距离,对每组元素各自进行直接插入排序。然后适当缩小gap,重复上述操作。直到gap等于1时,所有元素在同一组内最后一次直接插入排序。
2.2、图解分析
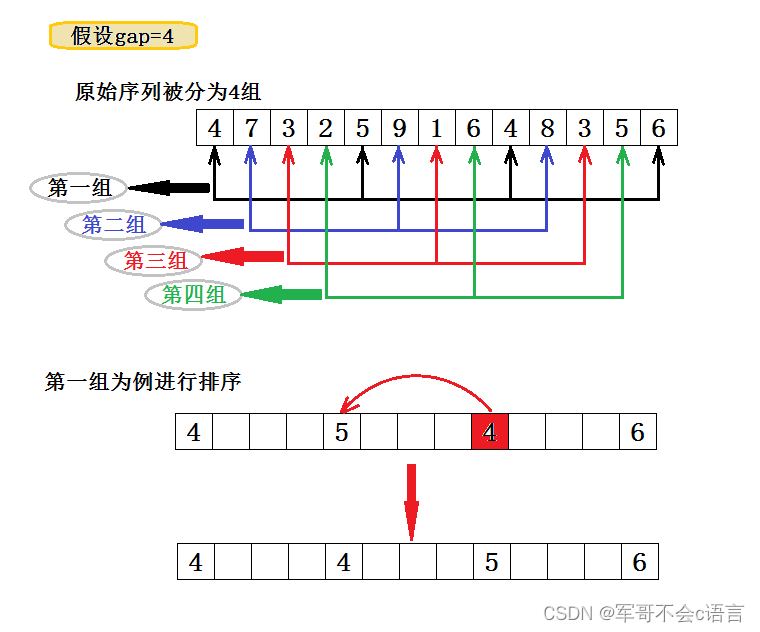
2.3、代码实现
// 希尔排序
void ShellSort(int* a, int n)
{
int gap = n;
while (gap > 1)
{
bool change = false;
gap = gap / 3 + 1;
for (int i = 0; i < n - gap; i++)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end-=gap;
change = true;
}
else
{
break;
}
}
a[end + gap] = tmp;;
}
if (change == false)
{
break;
}
}
}二、选择排序
基本思想:每次从待排序元素中选出最大(或最小)的一个元素将其存放在已有序序列的后一个位置,重复操作直到所有元素存放结束得到一个有序的新序列。
1、直接选择排序
1.1、排序方法
在元素集合arr[i]~arr[n-1]中选出关键码值最大(小)的元素,若该元素不是第一个(或最后一个),则将其与这组元素中的第一个(或最后一个)元素进行交换,对剩余未排序元素重复上述操作直到结束。
1.2、图解分析
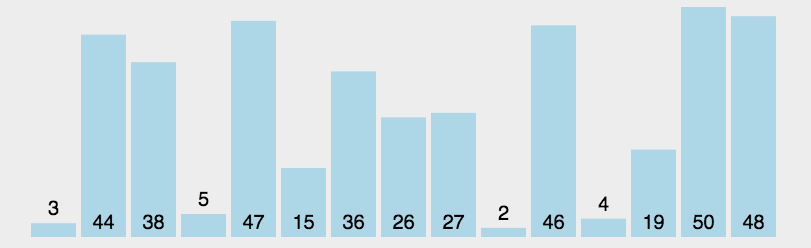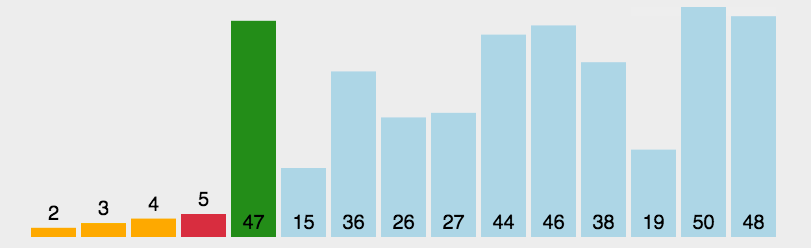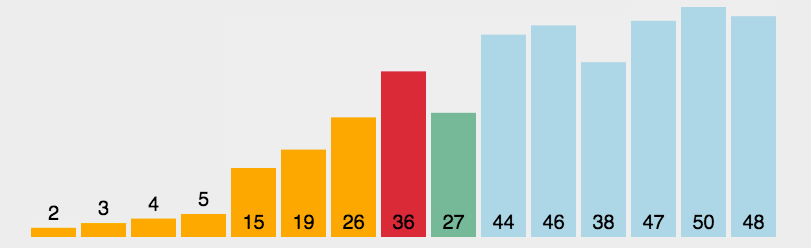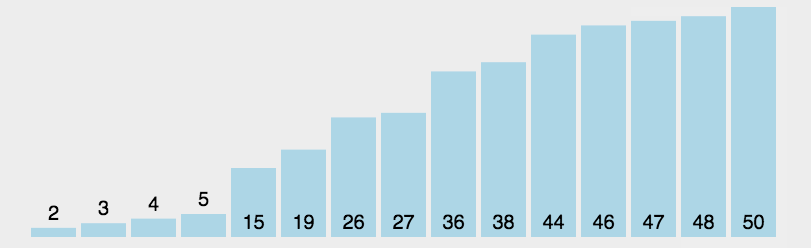
1.3、代码实现
// 选择排序
void SelectSort(int* a, int n)
{
int begin_i = 0;
int end_i = n-1;
while (begin_i < end_i)
{
int max_i = end_i;
int min_i = begin_i;
for (int i = begin_i; i <= end_i; i++)
{
if (a[i] < a[min_i])
{
Swap(&a[i], &a[min_i]);
}
if (a[i] > a[max_i])
{
Swap(&a[i], &a[max_i]);
}
}
begin_i++;
end_i--;
}
}2、堆排序
2.1、排序方法
堆排序的操作对象是堆,排序会调整部分节点在堆中的相对位置,为了不破坏堆的性质,我们将堆顶节点与堆的最后一个节点交换,再将除最后一个节点之外的其他节点通过向下调整算法调整成为一个新的堆。重复操作直到只剩下一个节点为止。
2.2、图解分析
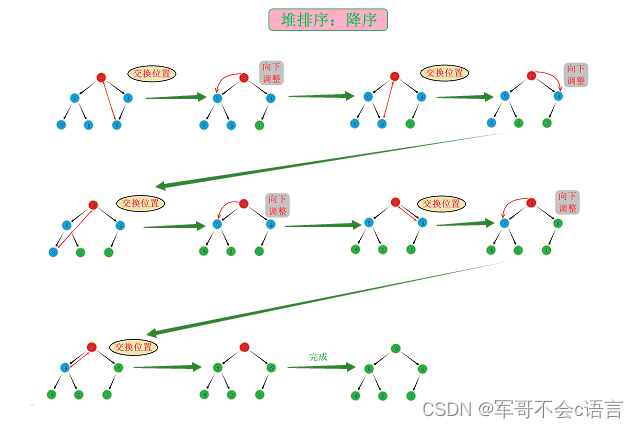
2.3、代码实现
//堆排序
typedef struct Heap
{
int* a;
int size;
int capacity;
}Heap;
//向下调整算法
void AdjustDwon(int* a, int n, Heap* hp)
{
for (int parent = (n - 2) / 2; parent >= 0; parent--)
{
int child = parent * 2 + 1;
while (child < n)
{
bool change = false;
if (child + 1 < n)
{
child = hp->a[child] > hp->a[child + 1] ? child : child + 1;
}
if (hp->a[child] > hp->a[parent])
{
int tmp = hp->a[parent];
hp->a[parent] = hp->a[child];
hp->a[child] = tmp;
change = true;
parent = child;
child = parent * 2 + 1;
}
if (change == false)
{
break;
}
}
}
}
//初始化堆
void InitialHeap(Heap* hp,int n)
{
if (!hp)
{
return;
}
int* tmp = (int*)malloc(sizeof(int) * n);
if (!tmp)
{
perror("InitialHeap::malloc:");
return;
}
hp->a = tmp;
hp->size = 0;
hp->capacity = n;
}
//创建堆
void HeapBuild(Heap* hp, int* a, int n)
{
assert(hp);
for (int i = 0; i < n; i++)
{
hp->a[i] = a[i];
}
AdjustDwon(a, n, hp);
}
//排序
void Sort(Heap* hp, int* a, int n)
{
int end = n - 1;
while (end > 0)
{
int tmp = hp->a[0];
hp->a[0] = hp->a[end];
hp->a[end] = tmp;
a[end] = hp->a[end];
end--;
AdjustDwon(a, end, hp);
}
a[0] = hp->a[0];
}三、交换排序
基本思想:根据序列中两个元素的关键码值的大小来判断是否需要交换他们在序列中的位置,默认将关键码值较大的元素向序列的尾部移动,关键码值较小的元素向序列的首部移动。
1、冒泡排序
1.1、排序方法
冒泡排序是将待排序元素的关键码值最大(小)的元素通过从前往后依次两两比较交换到最后面的位置。每操作一次可以确定一个元素在有序序列中的的位置。
1.2、图解分析
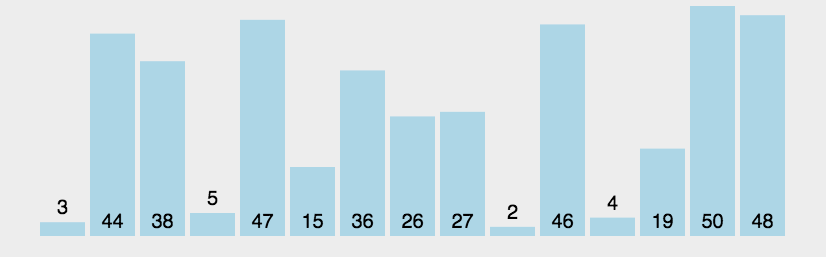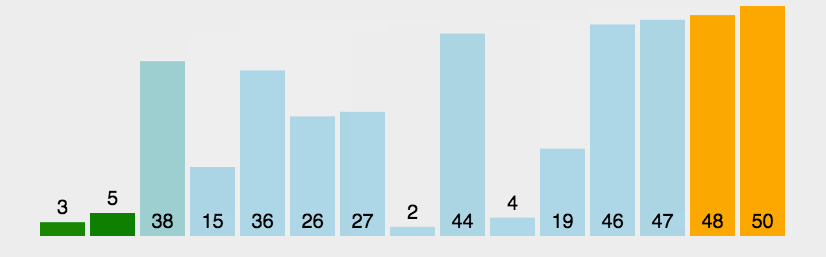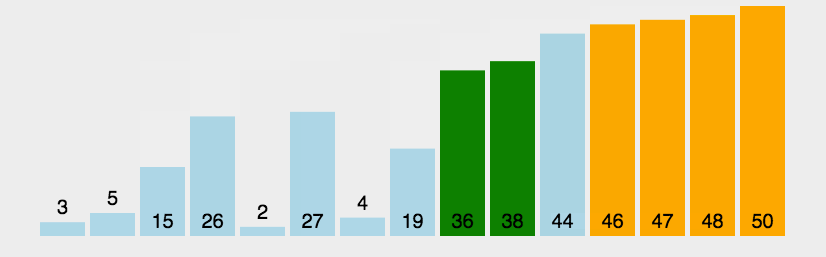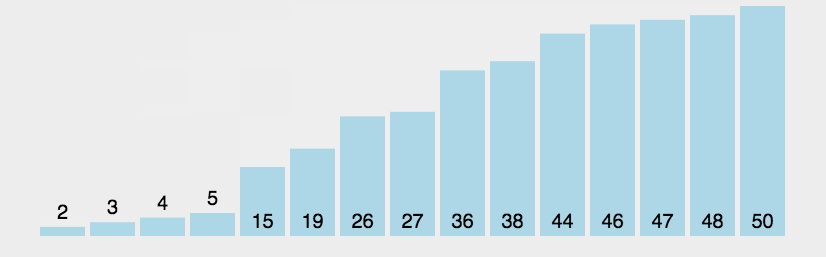
1.3、代码实现
// 冒泡排序
void BubbleSort(int* a, int n)
{
for (int j = 1; j < n; j++)
{
for (int i = 0; i < n - j; i++)
{
if (a[i] > a[i + 1])
{
int tmp = a[i];
a[i] = a[i + 1];
a[i + 1] = tmp;
}
}
}
}2、快速排序
基本思想:快速排序是任取待排序元素序列中的某元素的关键码值作为基准值,按照该基准值将待排序集合分割成左右两个子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,再对左右子序列重复该过程直到结束。
2.1、hoare排序
2.1.1、图解分析
key选左边,从右边出发。保证了相遇位置的值比key位置的值小;
key选右边,从左边出发。保证了相遇位置的值比key位置的值大;
(注意:key指的是下标)
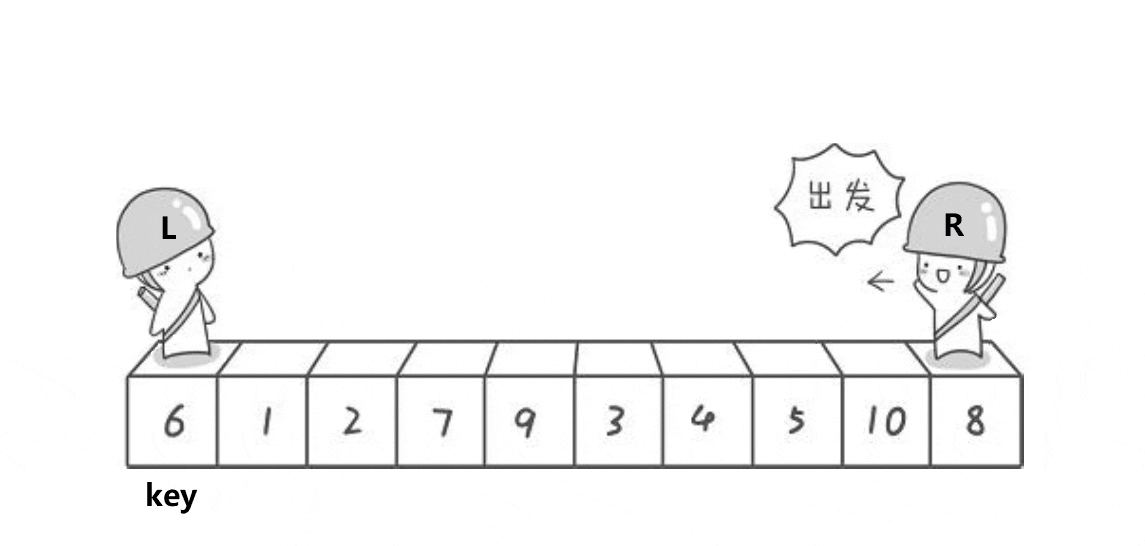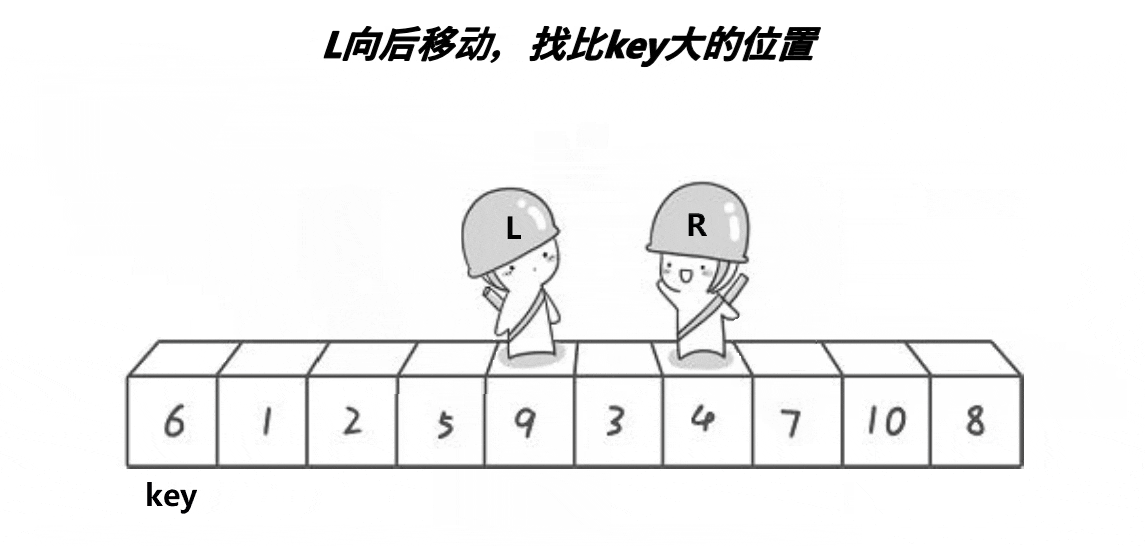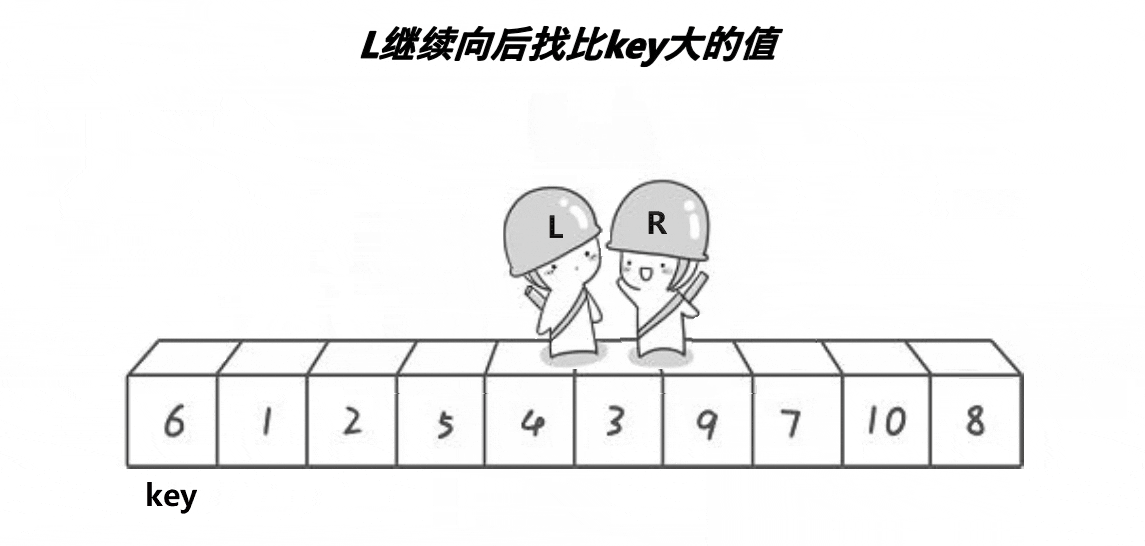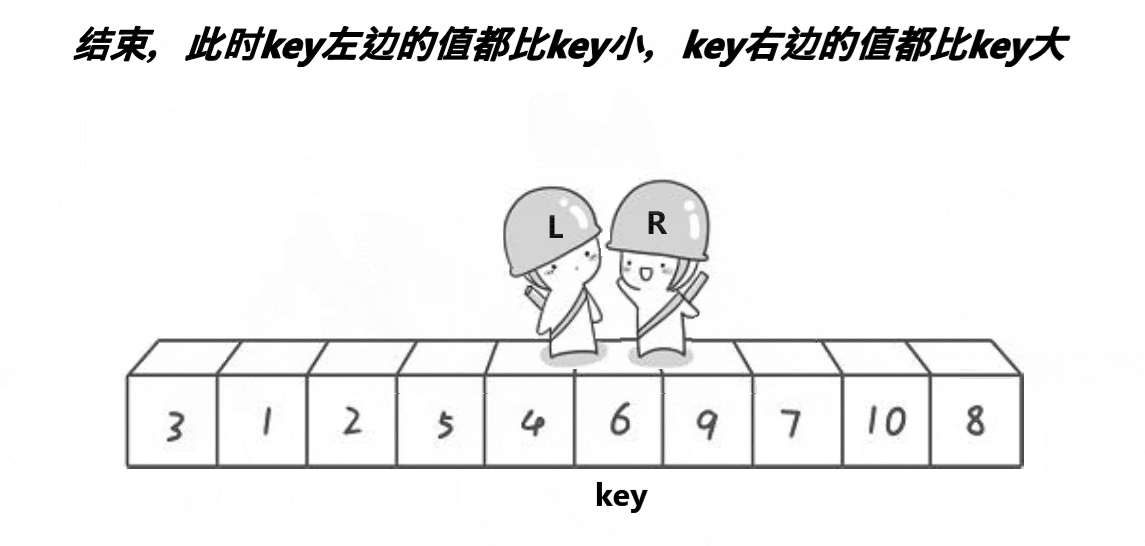
2.1.2、代码实现
// 快速排序hoare版本
int PartSort1(int* a, int left, int right)
{
int key = left;
while (left < right)
{
while (left < right && a[right] >= a[key])
{
right--;
}
while (left<right && a[left]<=a[key])
{
left++;
}
int tmp = a[right];
a[right] = a[left];
a[left] = tmp;
}
int tmp = a[key];
a[key] = a[left];
a[left] = tmp;
return left;
}2.2、挖坑法
2.2.1、图解分析
( 注意: 这里的key是一个变量,不是下标)
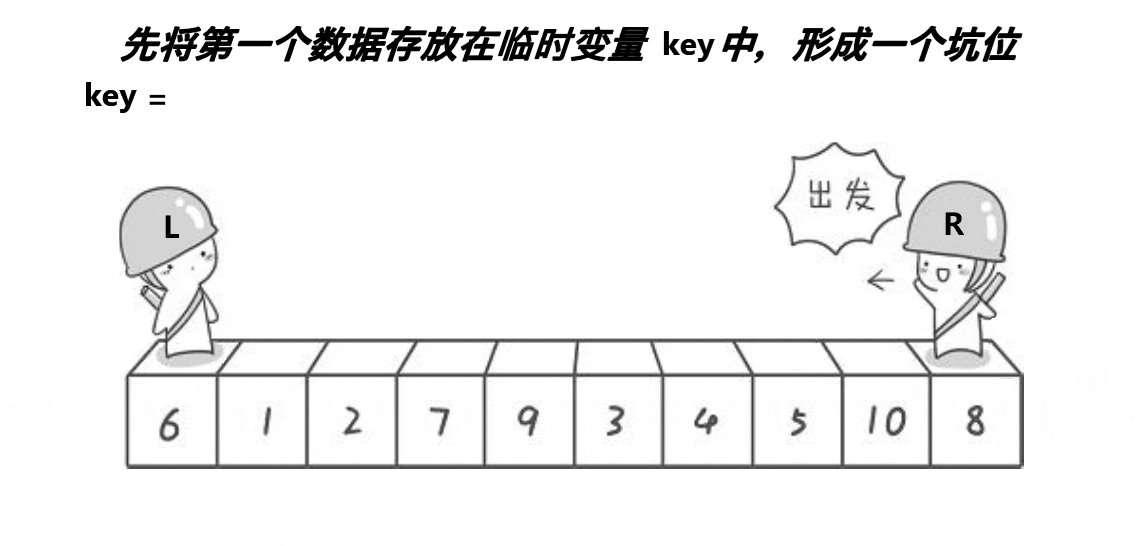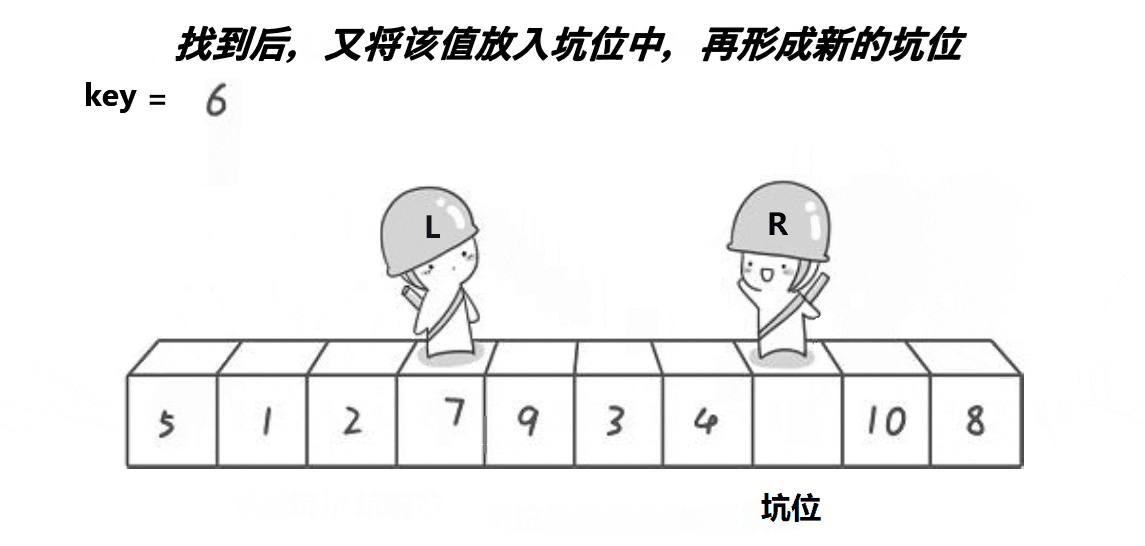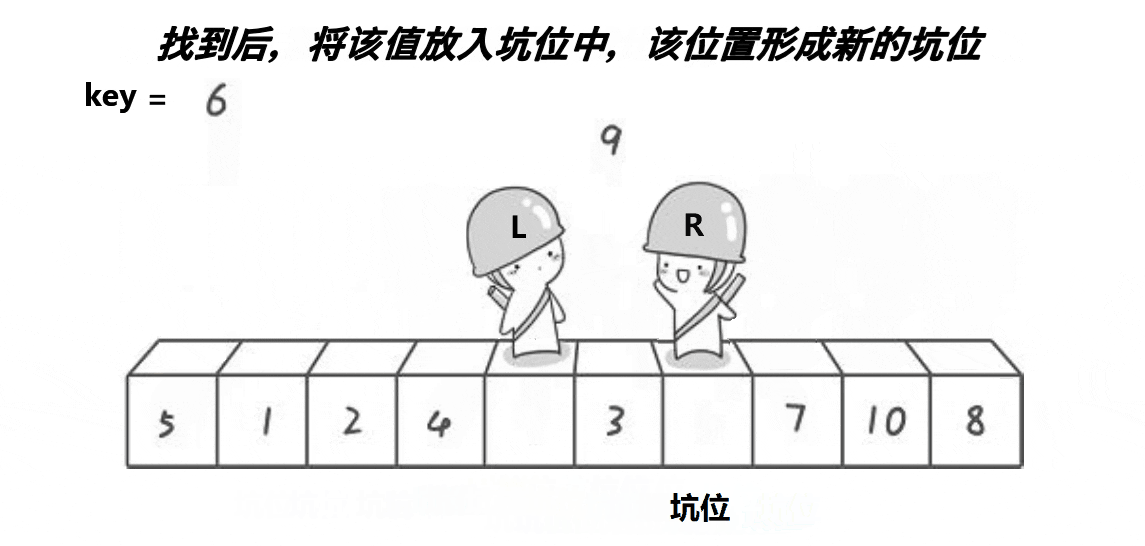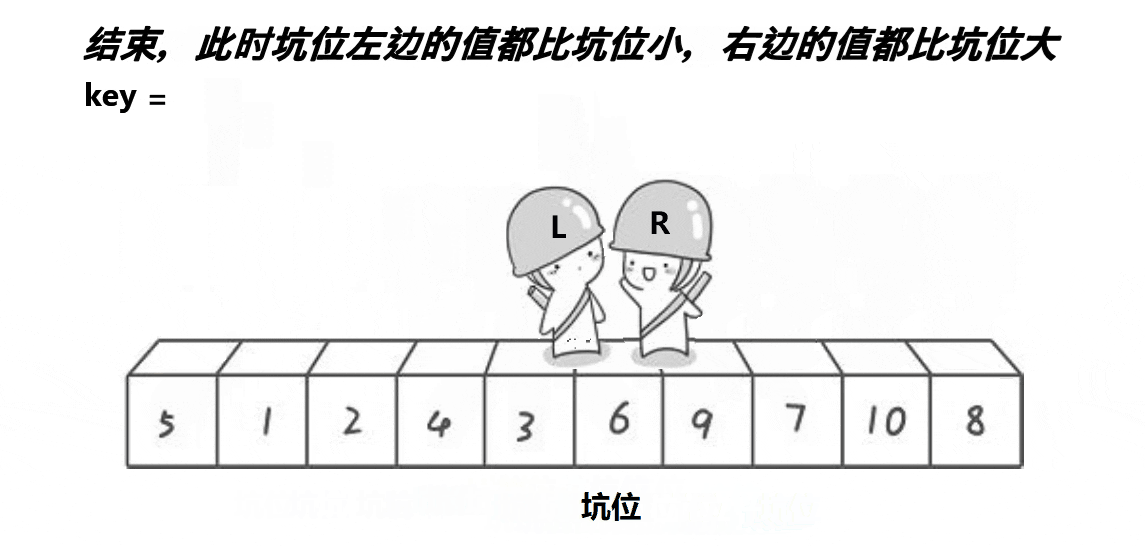
2.2.2、代码实现
// 快速排序挖坑法
int PartSort2(int* a, int left, int right)
{
int key = a[left];
int hole = left;
while (left < right)
{
while (hole < right)
{
if (a[right] < key)
{
a[hole] = a[right];
hole = right;
break;
}
right--;
}
while (hole > left)
{
if (a[left] > key)
{
a[hole] = a[left];
hole = left;
break;
}
left++;
}
}
a[hole] = key;
return hole;
}2.3、前后指针法
2.3.1、图解分析
(这里的key同样是一个变量,不是下标)

2.3.2、代码实现
// 快速排序前后指针法
int PartSort3(int* a, int left, int right)
{
int prev = left;
int cur = prev + 1;
int key = a[left];
while (cur <= right)
{
if (a[cur] < key)
{
prev++;
int tmp = a[prev];
a[prev] = a[cur];
a[cur] = tmp;
}
cur++;
}
a[left] = a[prev];
a[prev] = key;
return prev;
}四、归并排序
1、排序方法
归并排序是建立在归并操作上的一种排序算法。归并排序是将已有序的子序列合并,得到完全有序的序列;即先使每个字序列有序,再使子序列段间有序。归并排序的核心思想是先分解后合并。
2、图解分析
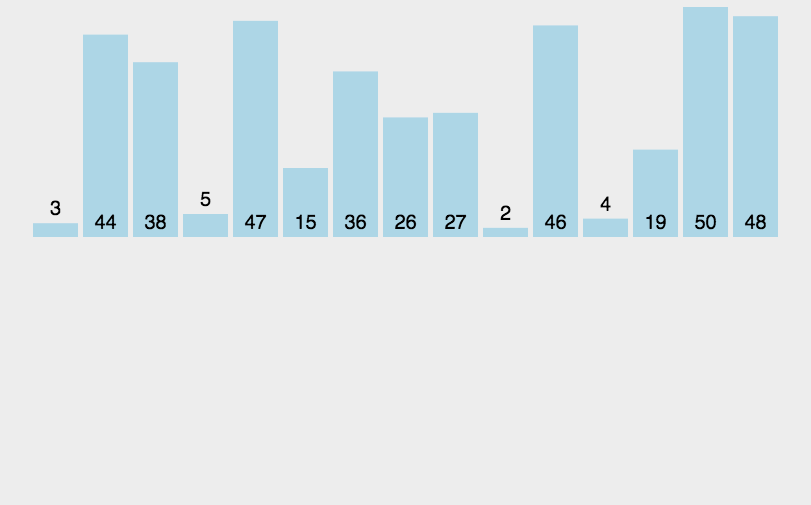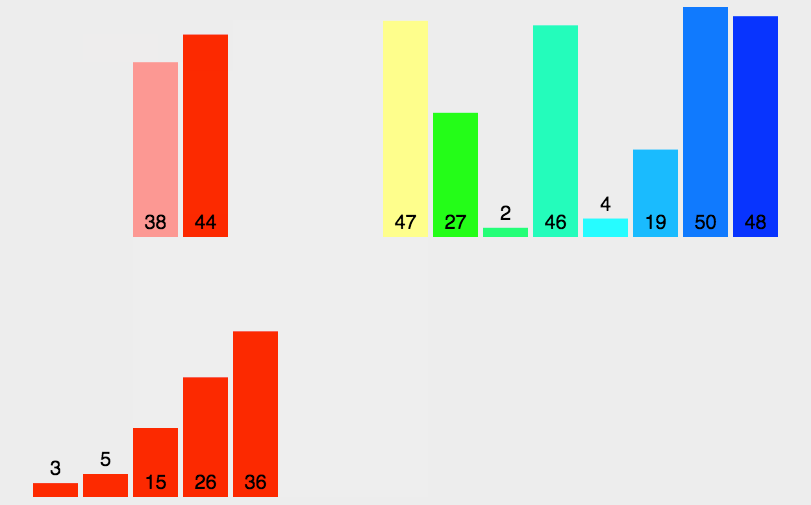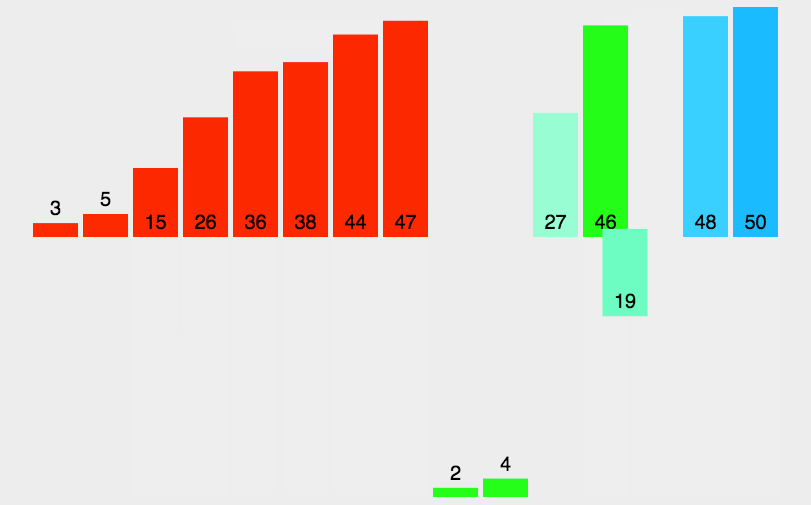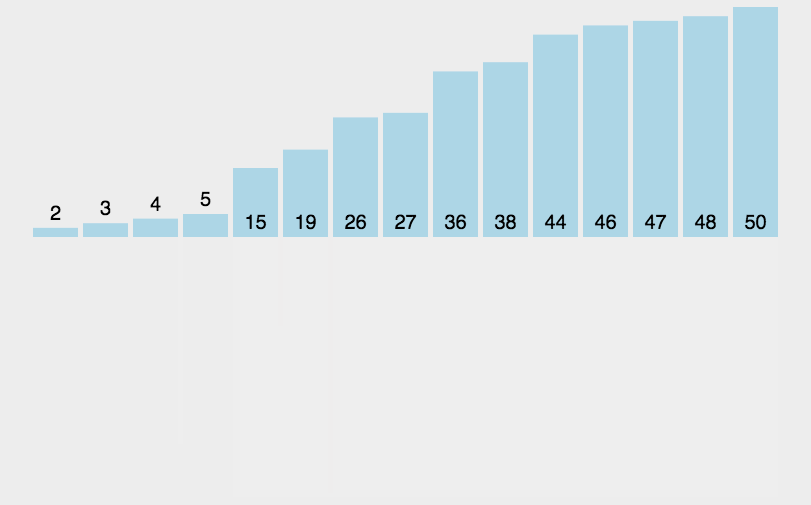
3、代码实现
// 归并排序递归实现
void _MergeSort(int* a, int begin, int end, int* tmp)
{
if (begin >= end)
{
return;
}
int mid = (begin + end) / 2;
_MergeSort(a, begin, mid, tmp);
_MergeSort(a, mid + 1, end, tmp);
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
int i = begin;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("MergeSort-->malloc:");
return;
}
_MergeSort(a, 0, n - 1, tmp);
free(tmp);
tmp = NULL;
}