目录

1 概述

2 系统模型 

2.1 单价模型

2.2 效用模型和 能源消费者（EC） 的目标

2.3 成本模型和 中央电站（CPS） 的目标

2.4 优化问题

3 优化的能源管理模型

4 模型的特性

4.1 均衡的存在

4.2 决策过程

5 算法

6 数值的仿真实现

---

1 概述

本文提出了一种智能电网中用户对电网系统的能源管理技术。为了鼓励消费者在能源短缺的情况下自愿参与与中央电站（CPS）的能源交易，将消费者的利益作为首要考虑。我们提出了一个新的系统模型，在社会最优的目标下激励能源交易。提出了一种以社会最优为目标的激励能源交易的新系统模型。然后研究了单领导跟随者 Stackelberg 博弈，以模拟 CPS 和多个能源消费者 (EC) 之间的交互，并基于系统模型找到优化问题的最优分布式解决方案。 CPS 被认为是寻求最小化其从 EC 购买能源的总成本的领导者，而 EC 是决定他们将向 CPS 出售多少能源以最大化其效用的追随者。结果表明，可以分布式实施的博弈具有社会最优解，其中所有消费者的收益总和最大化，而 CPS 的总成本最小化。数值分析证实了方法的有效性。

智能电网实施的关键因素是通过鼓励消费者为主电网提供辅助服务，使他们能够参与其中。基于消费者的积极参与，开发新的能源管理应用和服务，可以帮助利用智能电网的技术和能力升级。在一个受限的能源市场中，消费者参与能源管理可以大大增强电网的可靠性，并显著提高整个系统的社会效益。例如，一家公司的一项研究表明，在美国范围内，所有客户积极参加能源管理项目，每年可以实现100-150亿美元的效益。

智能电网背景下的能源管理最近受到了相当大的关注。然而，智能电网中成功的能源管理的关键挑战之一是激励消费者积极和自愿地参与这种管理计划。如果消费者对积极参与能源管理不感兴趣，智能电网的好处将不会被充分实现。因此，为了使消费者成为任何能源管理计划的组成部分，该计划的设计需要以消费者为中心，即智能电网利益的主要接受者是能源消费者，他们既是能源网的买方，又是能源网的卖方。

在本文中，针对消费者到电网系统提出了一种以消费者为中心的能源管理方案，该方案为积极参与智能电网的消费者带来了显着的利益。以消费者为中心的智能电网 (CCSG) 的概念最初是在2000年提出。此外，在对智能电网的客户域分析以及该域中出现的任务进行了研究。在本文中的能源管理方案通过提出歧视性定价策略来鼓励尽可能多的能源消费者（EC）参与与中央单位的能源交易，从而补充了 CCSG 的现有工作。在提议的定价机制中，剩余能源较少的 EC 可能期望更高的单位销售价格，并且价格与参与 EC 的数量及其出售的能源相适应。同时，我们的方案还旨在最大限度地降低中央电站（CPS）的总采购成本。本文介绍的工作显着扩展了之前的工作。它提供了改进和通用的系统模型，基于模型的解决方案的详细性能分析，以及更全面的仿真结果。

本文的主要工作：

1) 提出了一个通用系统模型，以促进以消费者为中心的能源管理。提出了新的效用和成本模型来实现歧视性定价机制。这些模型在反映实际需求和提供数学易处理性方面取得了很好的平衡；

2) 提出了一种单领导多追随者 Stackelberg 博弈，通过 CPS 和 EC 之间的有限交互实现分散决策，从而解决上述能源管理问题；

3）证明了基于Stackelberg博弈的算法的最优性和收敛性；

4) 通过分析和数值结果获得系统模型中参数选择的见解。 

本文的其余部分组织如下。第二节介绍了系统模型和优化问题。第三节描述了进行这种优化的能源管理模型的建议。第四节讨论了该模型的特性。第五节描述了一种实现社会最优的算法，第六节给出了数值仿真结果。最后，在第七节中提出了一些结论和对未来的展望。

2 系统模型 

2.1 单价模型

2.2 效用模型和 能源消费者（EC） 的目标

2.3 成本模型和 中央电站（CPS） 的目标

2.4 优化问题

---

3 优化的能源管理模型

4 模型的特性

4.1 均衡的存在

4.2 决策过程

---

5 算法

6 数值的仿真实现

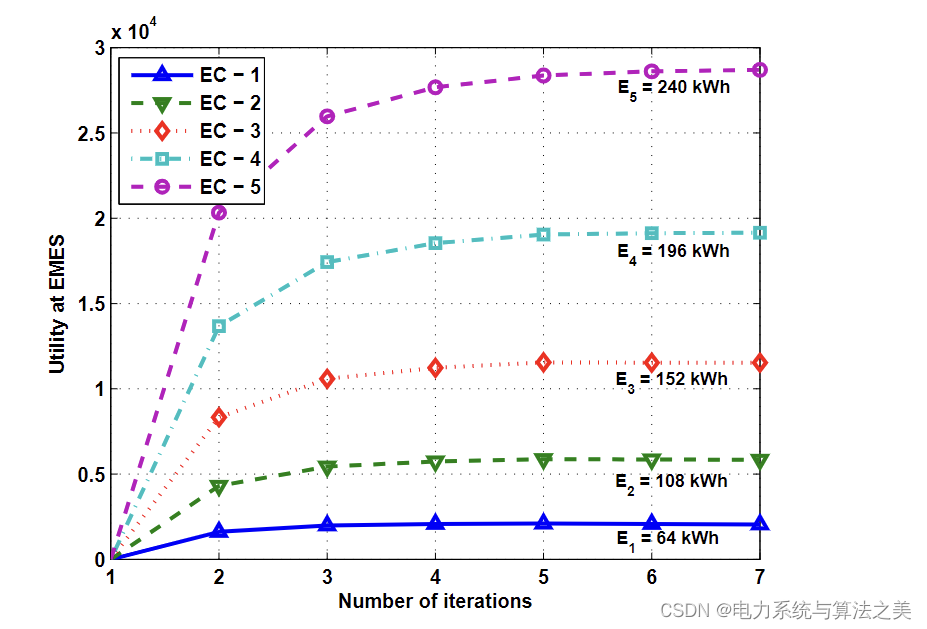
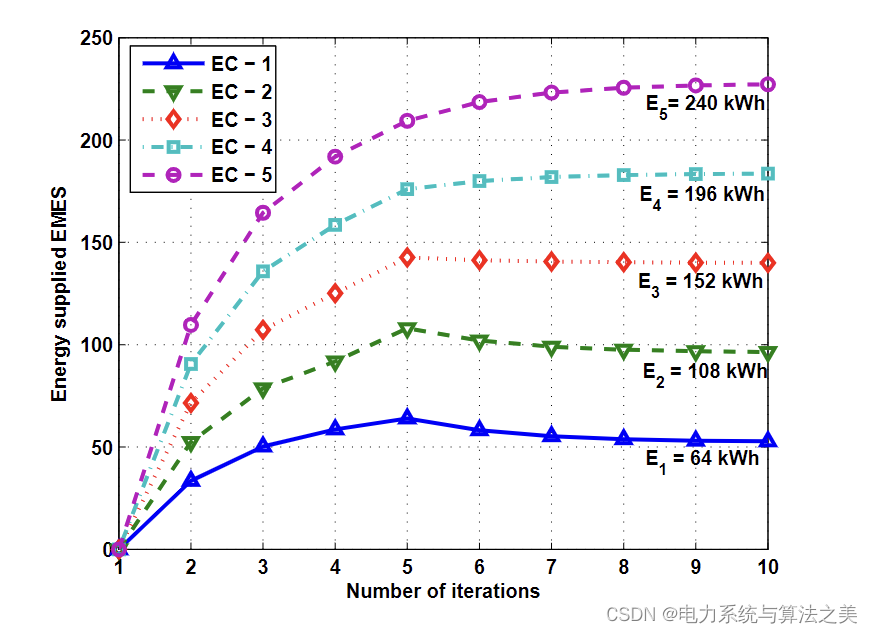
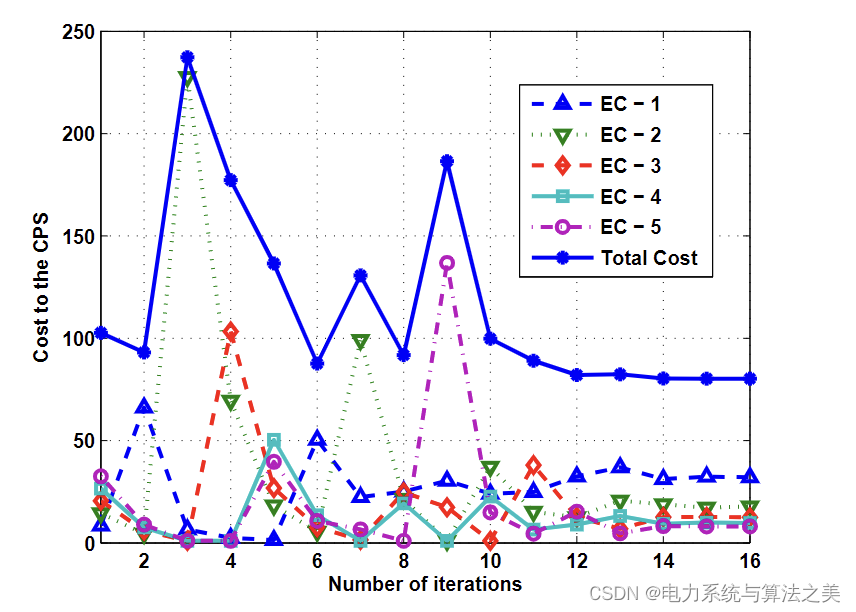
给出一个算例，其中许多 EC 参与与 CPS 的能源交易，其在几个特定的时间段内能源不足。假设任何 EC 的可用能量是 [64, 240] kWh 范围内的均匀分布随机变量。其他参数选择为 Edef = 700 kWh，P = 185 美分/KWh，r = 2，cn = 0.5，pmax = P，pmin = 8.45 [23] 和 an = 1，bn = 1 对于所有 n，除非另有说明。请注意，总采购成本中的其他成本，例如与能源采购不足相关的成本，在模拟中不予考虑。如果考虑到这些成本，则需要仔细确定与它们相关的 P。使用 1000 次独立模拟运行，所有结果均在 EC 容量的所有可能随机值上进行平均分配，并且在任何迭代中均未观察到异常情况，例如未能出现解决方案。

图 1 展示了在随机模拟中每个 EC 实现的效用、每个 EC 出售的能源量以及 CPS 在能源交易过程中产生的成本的收敛。在本例中，能量不足为 Edef = 700 kWh，考虑 5 个 EC，可用能量的随机生成值在图中描绘为 E1 到 E5。从图 1(a) 和图 1(b) 可以看出，每个 EC 的效用和提供的能量都随着迭代的增加而线性增加，效用和提供的能量以类似的方式向平衡增加。具有更多可用能源的 EC 销售更多并实现更高的效用。在大约 6 次迭代后，提供的能量和实现的效用都收敛到 EMES。图 1(c) 显示了交易过程中由 CPS 确定的单位能源价格的变化。与在迭代中几乎单调增加的能量和效用曲线不同，单位能量价格波动很大，直到达到 EMES。图 1(c) 还清楚地表明，在 EMES 上实现了可区分的单位能源价格，验证了拟议方案的目标之一。 EC 出售的能源较少，提供较高的单位能源价格，以激励他们参与能源交易。