算法概述

所谓算法，即特定计算模型下，旨在解决特定问题的指令序列
输入 待处理的信息（问题）
输出 经处理的信息（答案）
正确性 的确可以解决指定的问题
确定性 任一算法都可以描述为一个由基本操作组成的序列
可行性 每一基本操作都可实现，且在常数时间内完成
有穷性 对于任何输入，经有穷次基本操作，都可以得到输出
…
程序未必是算法，例如发生死循环或者栈溢出时。

算法在满足基本要求时，最重要的是：速度尽可能快，存储空间尽可能少（效率）。

计算模型

两个主要方面：
1.正确性：算法功能与问题要求一致？
2.成本：运行时间 + 存储空间

计算成本： T ( n ) = max ⁡ { T ( P )   ∣   ∣ P ∣ = n } T(n)=\max \{T(P) \space \boldsymbol | \space |P| = n \} T(n)=max{T(P) ∣ ∣P∣=n} 遵守最坏情况分析原则。

特定问题，不同算法下，需要抽象出一种理想的平台或模型，不再依赖于种种具体因素，从而直接准确地描述、测量并评价算法。

渐进复杂度

随着问题规模地增长，运算成本增大
$T(n)=\mathcal{O}(f(n))\text{if }\exists c>0,n\gg 2,T(n)<c\cdot f(n)$

与 $T(n)$ 相比，$f(n)$更为简洁，但依然反应前者地增长趋势：

常系数可忽略：$\mathcal{O}(f(n))=(c\times f(n))$
低次项可忽略：$\mathcal{O}(n^a+n^b)=\mathcal{O}(n^a)，a>b>0$

1.常数复杂度为：$\mathcal{O}(1)$
算法不含转向（循环、调用、递归等），必顺序执行即复杂度为 $\mathcal{O}(1)$

2.对数复杂度为：$\mathcal{O}(\log n)$
$\forall c>0,log(n)=\mathcal{O}(n^c)$，因此对数复杂度无限接近于常数

3.多项式复杂度：$\mathcal{O}(n^c)$

4.指数复杂度：$\mathcal{O}(a^n)$
计算成本增长极快，通常认为不可以接受

复杂度增长速度

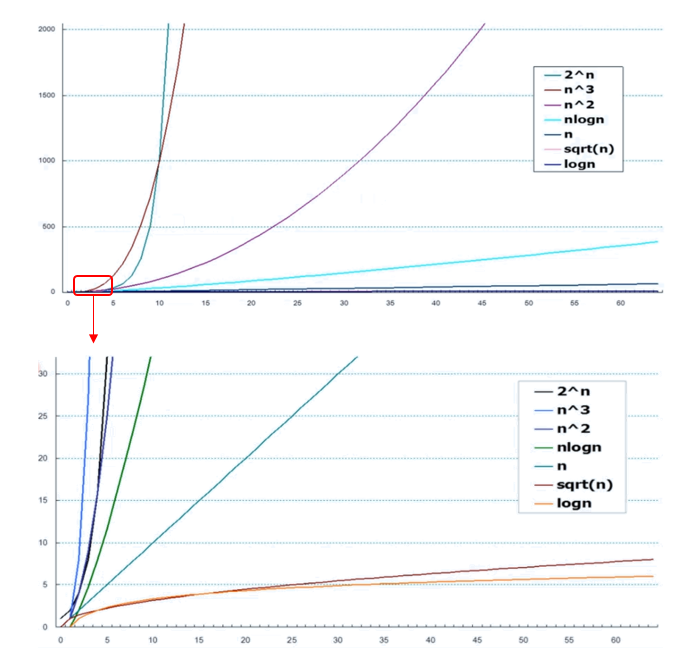
复杂度分析

算法分析的两个主要任务 = 正确性（不变性×单调性） + 复杂度

C++ 等高级语言的基本指令，均等效于常数条 RAM 的基本指令；在渐进意义下，两者相当。

复杂度分析的主要方法：
1.迭代：级数求和；
2.递归：递归追踪 + 递推方程；

实例：冒泡排序

问题：给定 n 个整数，将它们按（非降）序排列
观察：有序/无序序列中，任意/总有一对相邻元素顺序/逆序
思路：（扫描交换）依次比较每一个相邻元素，如果必要，交换之，若整躺扫描都没有进行交换，则排序完成；否则，再做一趟扫描交换。

void bubblesort(int A[],int n){
	for(bool sorted = false; sorted = !sorted; n--){	// 逐躺扫描交换，直至完全有序
		for(int i = 1; i< n; i++){	// 自左向右，逐对检查A[0,n)内各相邻元素
			if(A[i-1]>A[i]){	// 若逆序，则
				swap(A[i-1], A[i]);	//令其互换，同时
				sorted = false; //清楚（全局）有序标志	
			}
		}
	}
}

不变性：经过 k 轮扫描交换后，最大的 k 个元素必然就位；
单调性：经过 k 轮扫描交换后，问题规模缩减至 n-k；
正确性：经过最多 n 躺扫描后，算法必然终止，且能正确解答。

迭代与递归

递归跟踪分析：检查每个递归实例，累计所需时间（调用语句本身，计入对应的子实例），其总和即算法执行时间。

实例：数组求和（二分递归）

int sum(int A[], int lo, int hi){	//区间范围A[lo, hi]
	if(lo == hi) return A[lo];	//base case
	int mi = (lo + hi) >> 1;	//右移一位，相当于除以2 只有正数适用，而负数不适用
	return sum(A, lo, mi) + sum(A, mi+1, hi);
}	//入口形式为 sum(A,0,n-1)

master theorem

动态规划

实例：Fibonacci 序列

$$F(1)=1，F(2)=1,F(n)=F(n-1)+F(n-2)(n>=3，n\in N\ast )$$

计算Fibonacci数列的第n项（迭代版）：O(n)

__int64 fibI ( int n ) { 
   __int64 f = 1, g = 0; //初始化：fib(-1)、fib(0)
   while ( 0 < n-- ) { g += f; f = g - f; } //依据原始定义，通过n次加法和减法计算fib(n)
   return g; //返回
}

计算Fibonacci数列的第n项（二分递归版）：O(2^n)

__int64 fib ( int n ) { 
   return ( 2 > n ) ?
          ( __int64 ) n //若到达递归基，直接取值
          : fib ( n - 1 ) + fib ( n - 2 ); //否则，递归计算前两项，其和即为正解
}

计算Fibonacci数列第n项（线性递归版）：O(n)

__int64 fib ( int n, __int64& prev ) { //入口形式fib(n, prev)
   if ( 0 == n ) //若到达递归基，则
      { prev = 1; return 0; } //直接取值：fib(-1) = 1, fib(0) = 0
   else { //否则
      __int64 prevPrev; prev = fib ( n - 1, prevPrev ); //递归计算前两项
      return prevPrev + prev; //其和即为正解
   }
} //用辅助变量记录前一项，返回数列的当前项，O(n)

//Fib.h
using Rank = unsigned int;

class Fib { //Fibonacci数列类
private:
   Rank f, g; //f = fib(k - 1), g = fib(k)。均为int型，很快就会数值溢出
public:
   Fib ( Rank n ) //初始化为不小于n的最小Fibonacci项
   { f = 1; g = 0; while ( g < n ) next(); } //fib(-1), fib(0)，O(log_phi(n))时间
   Rank get()  { return g; } //获取当前Fibonacci项，O(1)时间
   Rank next() { g += f; f = g - f; return g; } //转至下一Fibonacci项，O(1)时间
   Rank prev() { f = g - f; g -= f; return g; } //转至上一Fibonacci项，O(1)时间
};

//main.c
#include<ctime>
#include<iostream>
using namespace std;

#include "Fib.h"

__int64  fibI ( int n ); //迭代版
__int64  fib ( int n ); //二分递归版
__int64  fib ( int n, __int64& f ); //线性递归版

int main ( int argc, char* argv[] ) { //测试FIB
// 检查参数
   if ( 2 > argc ) { fprintf ( stderr, "Usage: %s <Rank>\n", argv[0] ); return 1; }
   int n = atoi ( argv[1] );
// 依次计算Fibonacci数列各项
   printf ( "\n------------- class Fib -------------\n" );
   Fib f ( 0 );
   for ( int i = 0; i < n; i++, f.next() )
      printf ( "fib(%2d) = %d\n", i, f.get() );
   for ( int i = 0; i <= n; i++, f.prev() )
      printf ( "fib(%2d) = %d\n", n - i, f.get() );
   printf ( "\n------------- Iteration -------------\n" );
   for ( int i = 0; i < n; i++ )
      printf ( "fib(%2d) = %22I64d\n", i, fibI ( i ) );
   printf ( "\n------------- Linear Recursion -------------\n" );
   for ( int i = 0; i < n; i++ ) {
      __int64 f;
      printf ( "fib(%2d) = %22I64d\n", i, fib ( i, f ) );
   }
   printf ( "\n------------- Binary Recursion -------------\n" );
   for ( int i = 0; i < n; i++ )
      printf ( "fib(%2d) = %22I64d\n", i, fib ( i ) );
   return 0;
}

实例：LCS：最长公共子序列

两个字符串中找到最长的子序列，这里明确两个含义：
1.子串：表示连续的一串字符 。
2.子序列：表示不连续的一串字符。

1.两个字符串具有相同尾序，那么同时去掉两者的尾序，不影响它们的距离
2.如果 A 和 B 是不同的符号 ($A\ne B$)，则 $LCS(X^A,Y^B)$ 是以下两者的最大者：$LCS(X^A,Y),LCS(X,Y^B)$ ，适用于所有字符串 $X、Y$

给定两个字符串S1和S2，我们需要找到一个最长的子序列，该子序列同时出现在S1和S2中。这个子序列不要求在原字符串中是连续的，但在原字符串中的相对顺序必须与原字符串中的顺序相同。

举例说明：

假设有两个字符串：
S1 = “ABCBDAB”
S2 = “BDCAB”

它们的一个最长公共子序列是"BCAB"，它在两个字符串中都出现，而且是最长的。

LCS问题的目标是找到这个最长的公共子序列的长度以及可能的子序列之一。在动态规划中，可以使用一个二维表格来解决这个问题，表格中的值表示两个字符串在不同位置的字符之间的LCS长度。

通过解决LCS问题，我们可以解决许多实际应用，如文本比对、版本控制、DNA序列比对等。这个问题在算法设计和字符串处理中具有重要性。

#include <iostream>
#include <vector>
#include <string>

using namespace std;

string longestCommonSubsequence(string s1, string s2) {
    int m = s1.length();
    int n = s2.length();
    
    // 创建DP表，初始化为0
    vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
    
    // 填充DP表
    for (int i = 1; i <= m; ++i) {
        for (int j = 1; j <= n; ++j) {
            if (s1[i - 1] == s2[j - 1]) {
                dp[i][j] = dp[i - 1][j - 1] + 1;
            } else {
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
    }
    
    // 回溯构建最长公共子序列
    string lcs = "";
    int i = m, j = n;
    while (i > 0 && j > 0) {
        if (s1[i - 1] == s2[j - 1]) {
            lcs = s1[i - 1] + lcs;
            i--;
            j--;
        } else if (dp[i - 1][j] > dp[i][j - 1]) {
            i--;
        } else {
            j--;
        }
    }
    
    return lcs;
}

int main() {
    string s1 = "ABCBDAB";
    string s2 = "BDCAB";
    
    string result = longestCommonSubsequence(s1, s2);
    
    cout << "Longest Common Subsequence: " << result << endl;
    
    return 0;
}