基础优化算法

---

梯度下降

• 针对我们的模型没有显示解。（生活中很少能有完全符合的线性模型，大多数模型都是没有显示解的）
• 梯度：使函数的值增加最快的方向。
• 负梯度：使函数的值下降最快的方向。
• 学习率η：η沿着方向一次走多远。（η读作：yita）
• (-η * 倒数)为函数下降最快的地方。那么w0+(-η * 倒数)为w1的位置。
  

1.1 小批量随机梯度下降

• 每次求梯度时，需要对整个损失函数求导。这个损失函数是对我们所有样本的平均损失。意味着：求一次梯度，需要对整个样本算一遍。这个开销很大，很贵的事情。
  
  

1.2 小结

线性回归实现

1. 处理数据

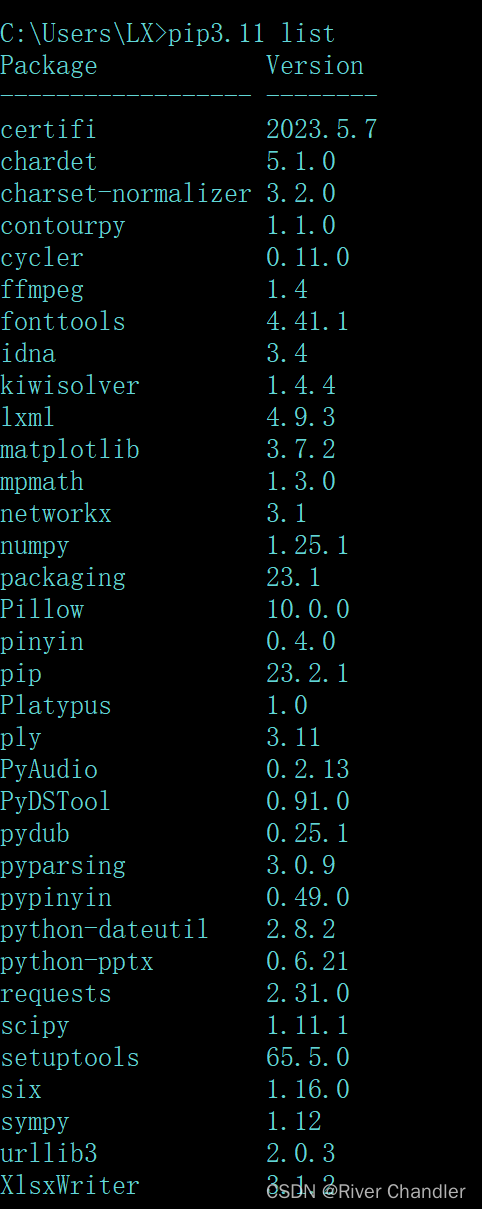
• 如果没有d2l包，需要进入cmd，以管理员身份运行。输入：pip install -U d2l -i https://mirrors.aliyun.com/pypi/simple/下载即可。
• 如果报：ModuleNotFoundError: No module named ‘torchvision’ ，直接在jupyter notebook中输入：pip install torchvision -i https://mirrors.aliyun.com/pypi/simple/
  
  

这段代码定义了一个名为synthetic_data的函数，用于生成合成数据。

该函数接受三个参数：

• w：一个一维张量（向量），表示模型的权重。
• b：一个标量，表示模型的偏置项。
• num_examples：整数，表示要生成的数据样本数量。

函数的主要步骤如下：

1. 使用torch.normal(0, 1, (num_examples, len(w)))生成形状为(num_examples, len(w))的服从标准正态分布的随机张量X，其中均值为0，标准差为1。
2. 使用矩阵乘法运算符torch.matmul(X, w)将X与权重w相乘，然后加上偏置项b，得到预测值y。
3. 使用torch.normal(0, 0.01, y.shape)生成形状与y相同的服从标准正态分布的随机噪声，并将其加到y上，以模拟真实数据的噪声。
4. 最后，使用y.reshape((-1, 1))将y转换为形状为(-1, 1)的二维张量，其中-1表示根据其他维度的大小自动计算该维度的大小。简单来说，reshape((-1,1))就是将数组转换成只有一列，行数不确定的二维数组。

函数返回生成的合成数据X和转换后的标签y。

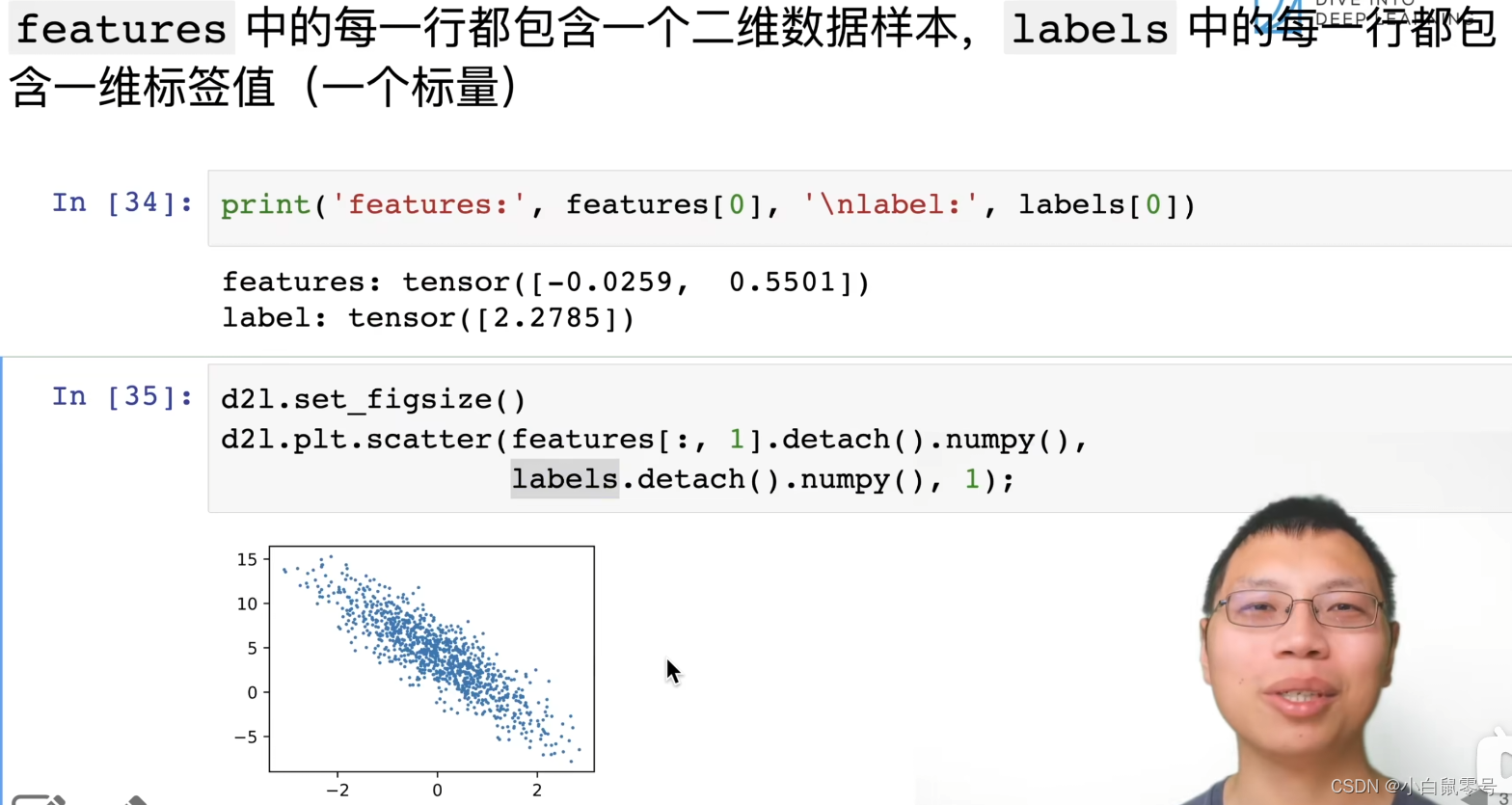
这段代码是使用 d2l 库绘制散点图的示例。

d2l.set_figsize() 用于设置图形的大小，可以指定宽度和高度。

d2l.plt.scatter(features[:,1].detach().numpy(), labels.detach().numpy(), 1) 这行代码绘制散点图，其中：

• features[:,1] 表示从特征矩阵中取出第二列数据作为 x 坐标；
• labels 表示标签数据；
• 1 表示散点的半径为 1。

detach() 方法将张量从计算图中分离出来，返回一个在内存中独立的张量，这样可以避免在绘图时修改原始数据。numpy() 方法将张量转换为 NumPy 数组，以便在绘图函数中使用。

1.3 生成大小为batch_size的小批量

这段代码定义了一个名为 data_iter 的函数，用于生成批量训练数据的迭代器。

函数接受三个参数：batch_size、features 和 labels。其中，batch_size 表示每个批次中的样本数量，features 是特征矩阵，labels 是标签向量。

首先，函数计算了样本总数 num_examples，然后创建了一个包含所有样本索引的列表 indices。接着，使用 random.shuffle() 方法将索引随机打乱。

接下来，函数使用一个循环来生成批次数据。在每次循环中，它从打乱后的索引列表中取出 batch_size 个索引，并将这些索引转换为一个张量 batch_indices。然后，函数使用 yield 语句返回当前批次对应的特征矩阵和标签向量。

由于使用了 yield 语句，该函数是一个生成器函数，可以在循环中逐个生成批次数据，而不需要一次性将所有数据加载到内存中。这样可以有效地减少内存占用，提高训练效率。

2. 处理模型

这段代码定义了两个 PyTorch 张量 w 和 b，用于神经网络中的线性回归模型。

w = torch.normal(0, 0.01, size=(2,1), requires_grad=True) 这行代码创建了一个形状为 (2,1) 的张量 w，其中的元素是从均值为 0、标准差为 0.01 的正态分布中随机采样得到的。requires_grad=True 表示需要计算该张量的梯度，以便在反向传播过程中更新参数。

b = torch.zeros(1, requires_grad=True) 这行代码创建了一个形状为 (1,) 的张量 b，其中的元素全部初始化为 0。requires_grad=True 表示需要计算该张量的梯度，以便在反向传播过程中更新参数。

在神经网络中，w 和 b 通常分别表示线性回归模型的权重和偏置项。通过不断迭代优化算法（如随机梯度下降），可以更新 w 和 b 的值，使得模型的预测结果越来越接近真实值。

3. 模型评估

这段代码定义了一个名为 sgd 的函数，用于执行小批量随机梯度下降算法。

函数接受三个参数：params、lr 和 batch_size。其中，params 是一个包含模型参数的列表或张量，lr 是学习率，batch_size 是每个批次中的样本数量。

函数使用 torch.no_grad() 上下文管理器来禁用梯度计算，以避免在反向传播过程中占用过多的内存。

接下来，函数使用一个循环遍历 params 中的每个参数。对于每个参数，它首先使用当前批次的梯度（即 param.grad）除以批次大小 batch_size，然后乘以学习率 lr，并从原始参数值中减去这个值，以更新参数。最后，使用 param.grad.zero_() 将该参数的梯度清零，以便在下一个迭代中使用新的梯度值。

总之，这段代码实现了一种简单的随机梯度下降算法，用于训练神经网络模型。

4. 训练过程

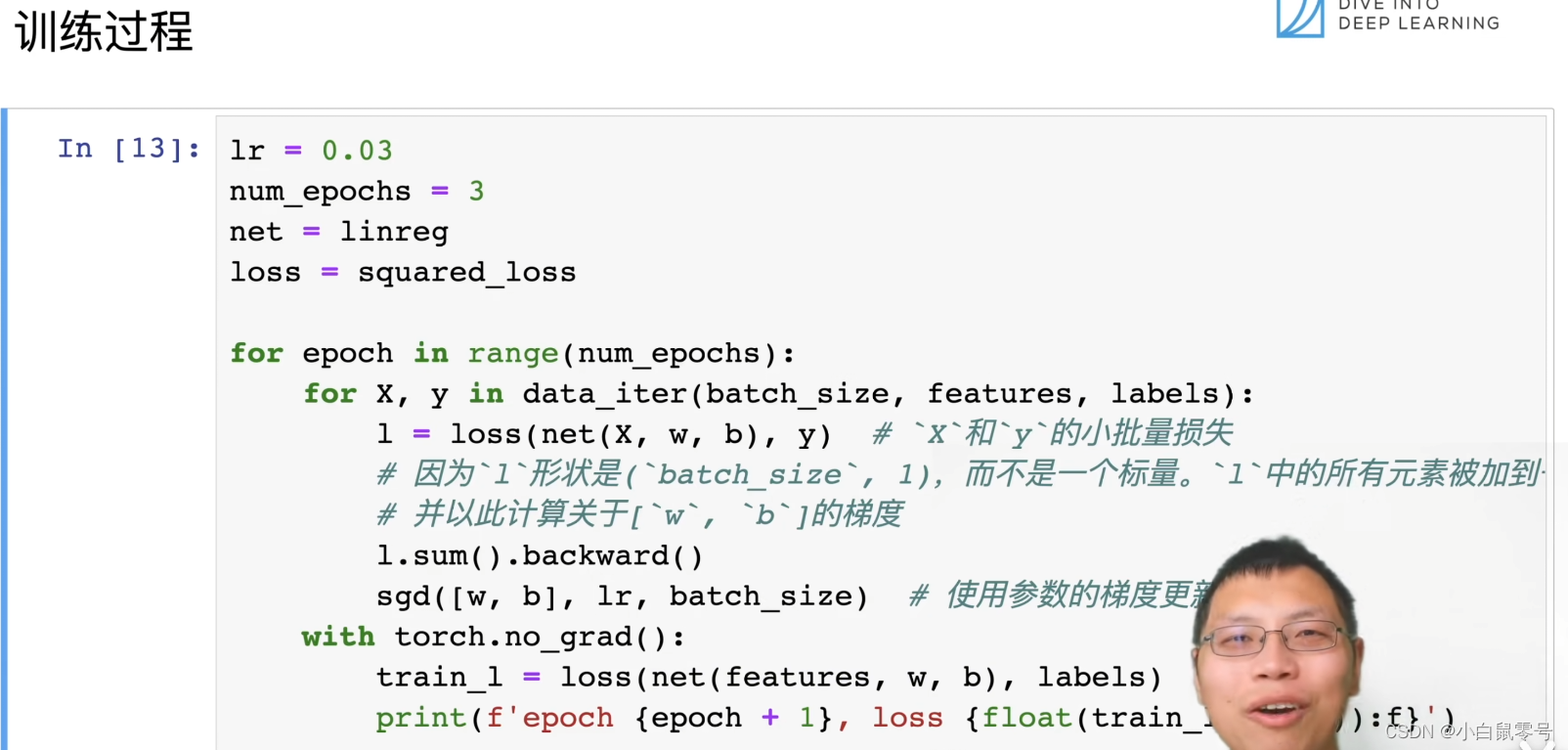
被挡住的代码为： print(f'epoch{epoch+1}, loss{float(train_l.mean()):f}')
这段代码是一个训练神经网络模型的完整流程，包括前向传播、计算损失、反向传播和参数更新。

首先，定义了一个 for 循环，用于迭代多个 epoch。在每个 epoch 中，使用 data_iter() 函数生成一批数据 X,y，其中 batch_size 是每个批次中的样本数量，features 是特征矩阵，labels 是标签向量。

接下来，对于每个数据点 X，使用 net(X,w,b) 进行前向传播，得到预测值 。然后，计算预测值与真实标签 y 之间的损失 loss(net(X,w,b),y)。

接着，调用 l.sum().backward() 对损失进行反向传播，计算出每个参数的梯度。然后，使用随机梯度下降算法 sgd([w,b], lr, batch_size) 更新参数 w 和 b。

在每个 epoch 结束后，使用 with torch.no_grad(): 上下文管理器将梯度计算关闭，以避免在输出训练过程中占用过多的内存。然后，使用 train_l = loss(net(features, w, b), labels) 计算当前模型在测试集上的损失，并打印出当前 epoch 和平均损失。

总之，这段代码实现了一个标准的神经网络训练过程，通过不断迭代优化算法来提高模型的性能。