文章目录
- 一、简介
- 二、实现代码
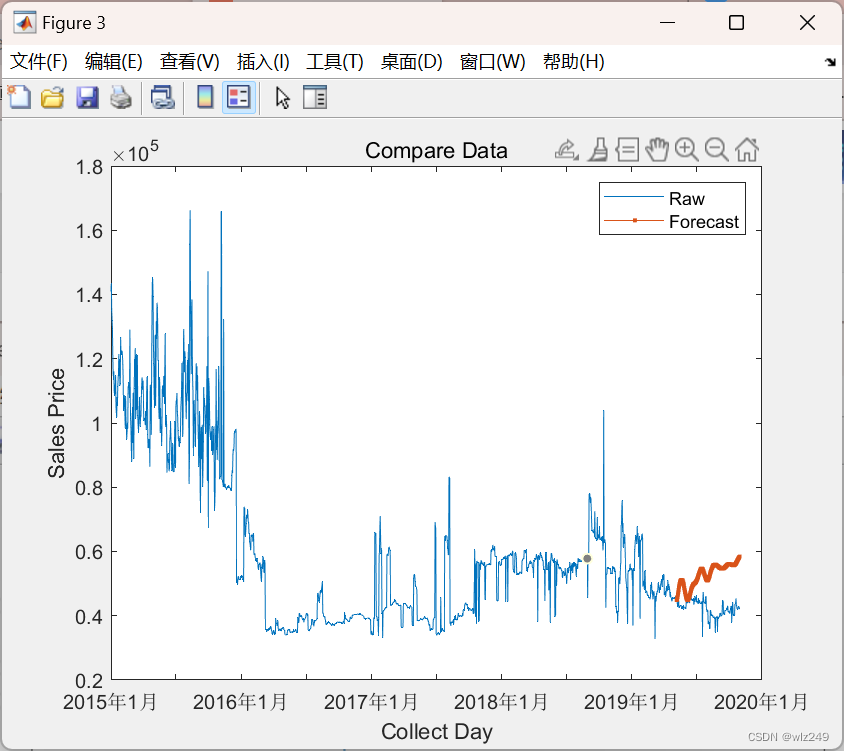
- 三、实现效果
- 参考资料
一、简介
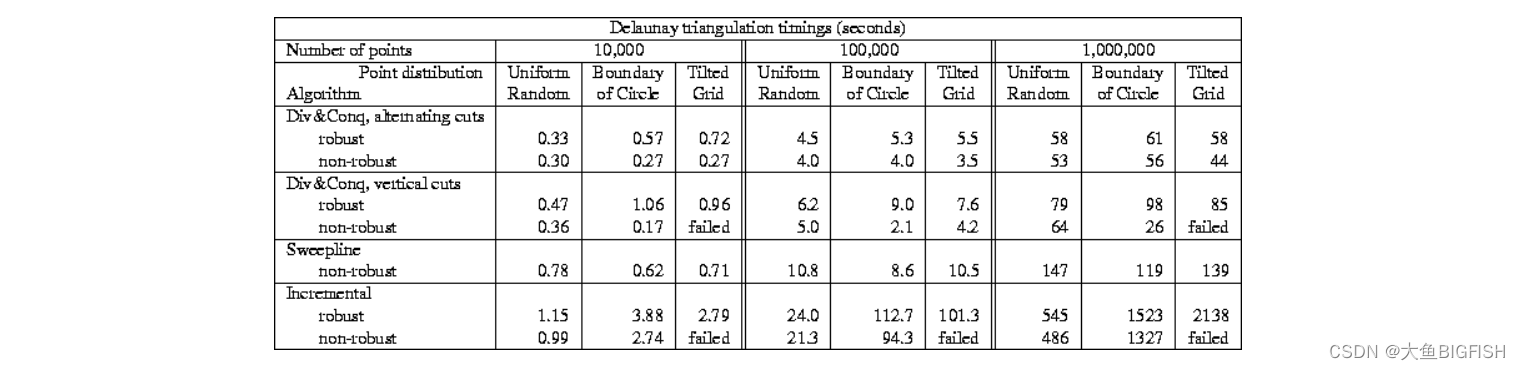
Delaunay三角网现有的构网算法有很多种,有学者曾对其中一些算法进行了调查和评估(如下图所示)。结果表明,在少量点时,Lawson的增量插入算法、Lee和Schachter的分治算法以及Fortune的平面扫描算法在速度上大致相当。但随着点数的增加,分治算法仍然保持着较为不错的计算效率,扫描线算法亦尚可,但增量插入算法已变得很差。因此,分治算法作为非常经典的三角网构网方法,非常值得进行学习一下。
1、删除重复点。所有的三角网实现算法都会采用这一步过程,如果不消除重复点,直接进行构网计算,很有可能会导致灾难性的错误,也会使得结果变得不可预知。分治算法采用的是根据点的x坐标对它们进行排序,然后基于此来检测和删除重复的点。
2、递归分治。在剔除重复点之后,递归地将输入的顶点进行减半,直到它们被划分为每两个或三个顶点的子集,这样每个子集都很容易被