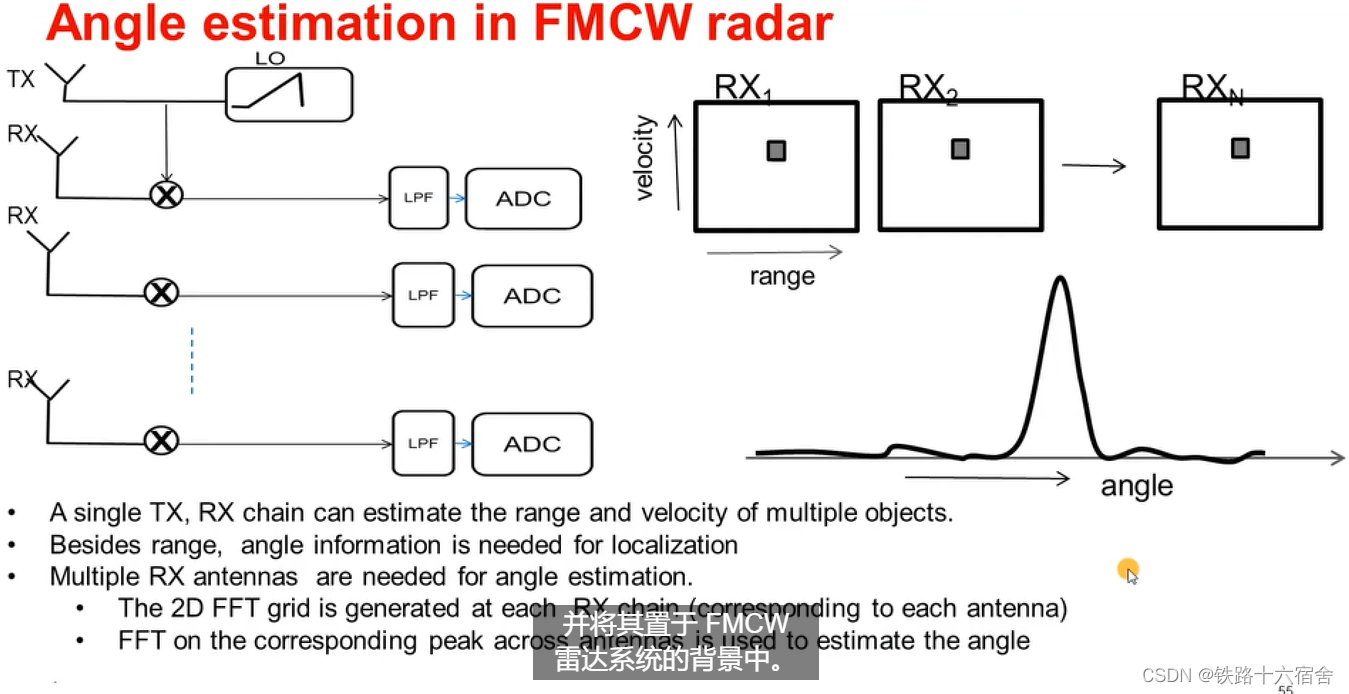
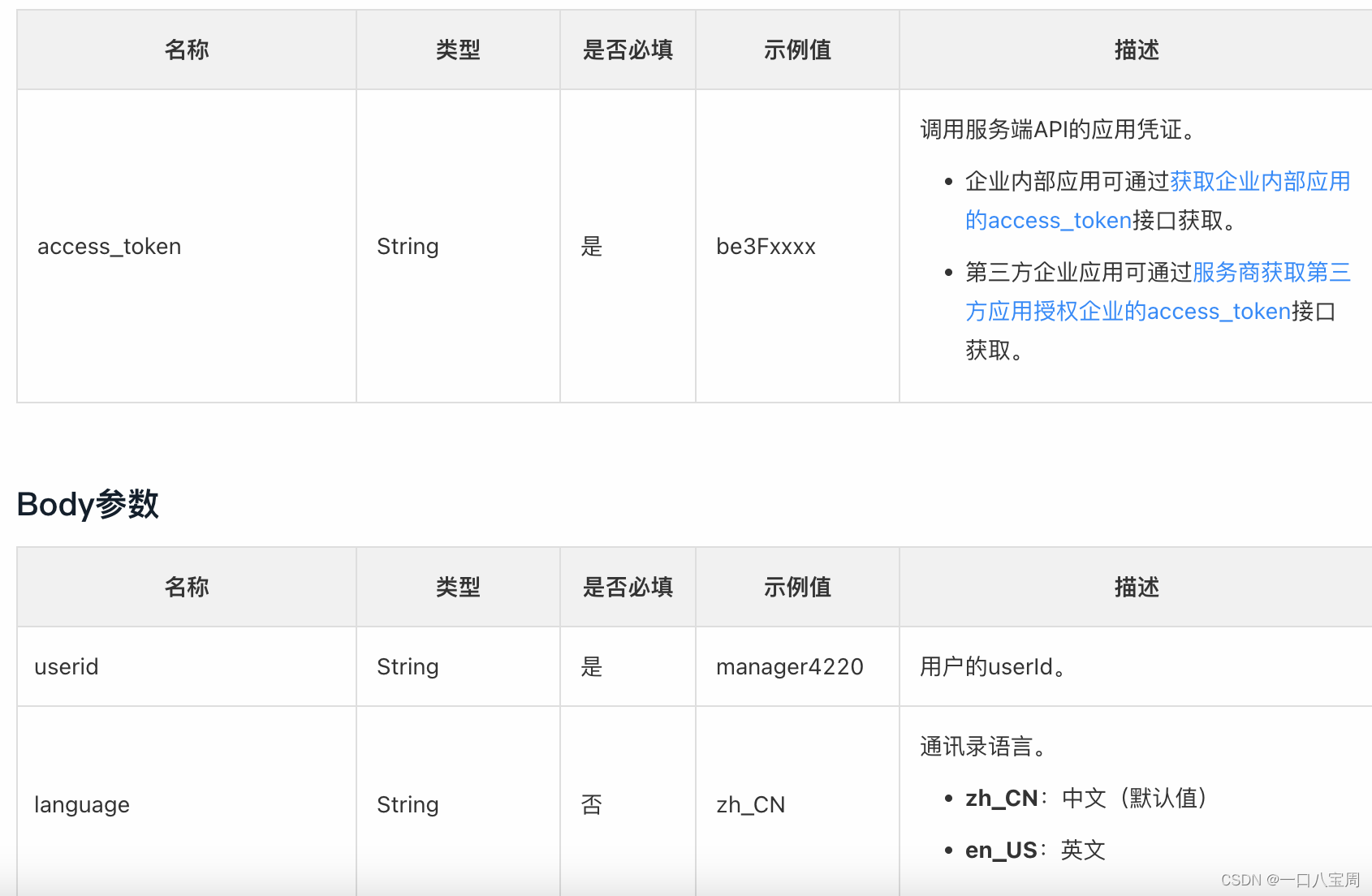
前边两篇博文从距离和速度两个维度进行了介绍，本篇将沿着第三个维度，角度进行分析，这也是毫米波传感器原理介绍的最后一篇理论基础。还是老规矩，我们先把公式列出来。

1. 假设雷达两个接收天线之间的距离为d，θ 是物体相对于雷达的达到角度，ω是两个接收天线中频信号的相位差，则有$\omega =\frac{2\pi dsin(\theta )}{\lambda }$,导出$\theta =si{n}^{-1}(\frac{\lambda \omega }{2\pi d})$
2. 与速度模糊类似，两个中频信号的相位差也需要小于π，则有$\frac{2\pi dsin(\theta )}{\lambda }<\pi$,可得出最大到达角的公式${\theta }_{max}=si{n}^{-1}(\frac{\lambda }{2d})$
3. N为阵列天线的数量，则到达角分辨率${\theta }_{res}=(\frac{\lambda }{Ndcos(\theta )})$,通常假设两个天线之间的距离为 λ 除以 2，并且 θ 为 0，则公式变为${\theta }_{res}=(\frac{2}{N})$。

到达角测量基础

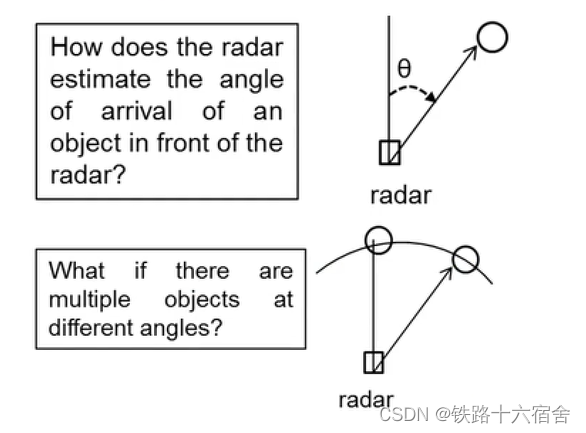
您有一个雷达，它前面有一个物体，雷达如何估算该物体的到达角？如果在不同的角度存在多个物体，但可能具有相同的距离和相同的相对速度，会怎么样？雷达的最大角度视场有哪些决定因素？雷达的角度分辨率取决于什么？这些问题我们都会在后续进行讨论。


我们在讨论雷达测速原理时，得出一个重要的结论：中频信号的相位对物体的距离的微小变化十分敏感。具体而言，物体距离的微小变化 Δd 会导致相位变化 ω，其值为 4πΔd除以 λ。
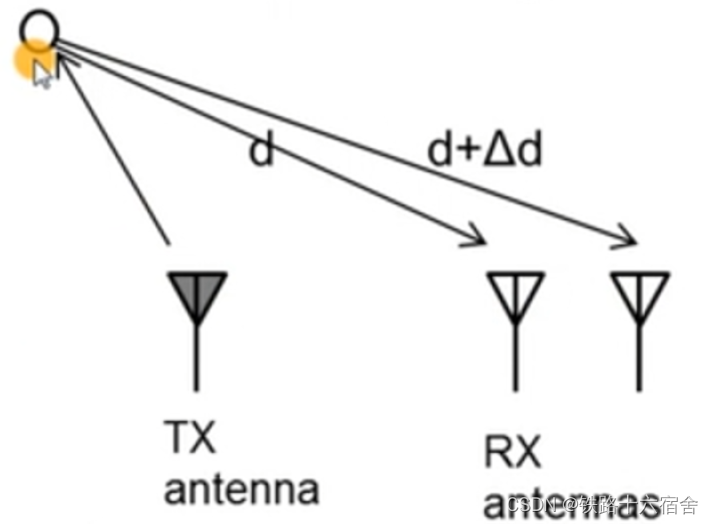
角度估算利用相同的原理，角度估算需要至少2个RX天线。这里是利用物体相对于雷达天线的距离差，过程如下图所示。由于接受天线之间存在一个距离，所以接收信号到达雷达不同天线的传播距离存在一个的差异$\Delta d$,，则两个天线之间的中频信号的相位差为$\omega =\frac{2\pi \Delta d}{\lambda }$，至于为什么分子的系数为2而不是4，那是因为只有发射回来的单程路径存在一个的距离差。

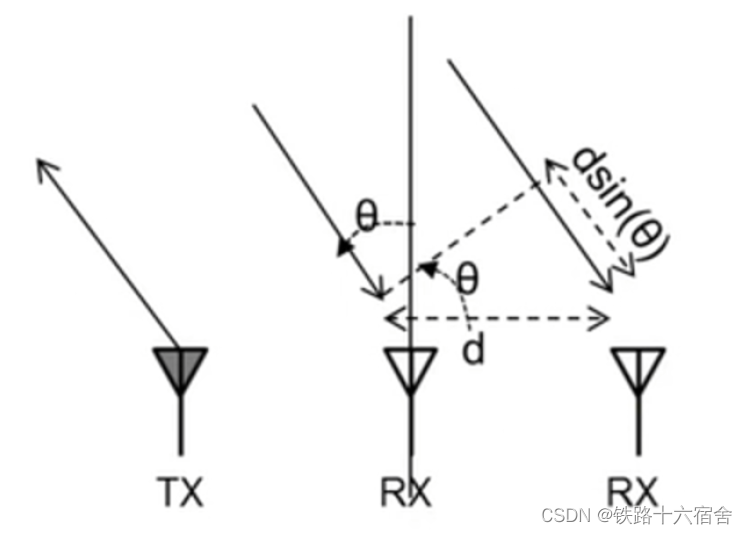
那这个距离和物体于雷达的角度存在什么样的关系？我们将雷达和物体的角度关系和变化的距离关系画出，如下图所示。在下图我们是假设雷达接收天线之间的距离为d，则接受信号到达雷达的两个接受天线的距离差公式为则有$\omega =\frac{2\pi dsin(\theta )}{\lambda }$,导出$\theta =si{n}^{-1}(\frac{\lambda \omega }{2\pi d})$

发射器天线发射一个线性调频脉冲帧，每个天线会接收该数据。每个天线会处理该数据，以创建一个 2D-FFT矩阵，其中包含与物体的距离和速度相对应的峰值。那么，两个接收天线，对应两个2D-FFT矩阵。请注意，两个2D-FFT峰值的位置几乎相同。这两个峰值之间的相位差将为2πdsin(θ)，dsin(θ) 是额外的距离，然后除以 λ。您通过比较这两个信号，这两个峰值处的信号来测量该相位差之后，根据上面得到的公式，便可以计算到达角。

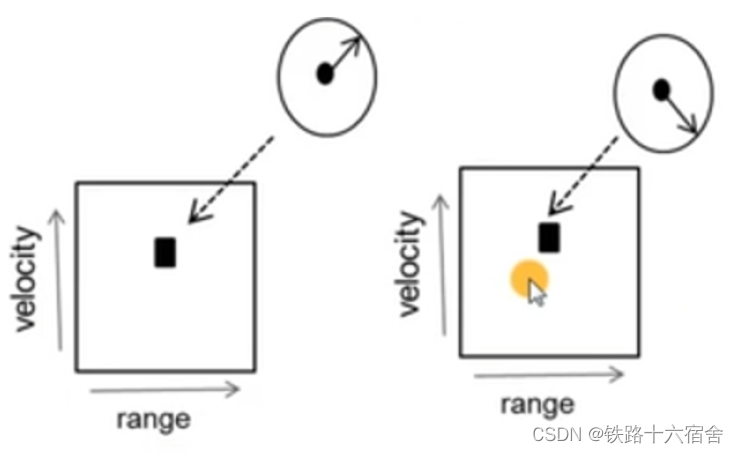
现在思考一个问题，如果在雷达前方存在两个物体，两个物体离雷达的距离相同并且速度也相同。上诉的方法还可以识别出两个物体的角度吗？ 答案是否定的，对于两个天线而言，只能区分一个距离一个速度的上的一个物体角度，如果需要同一距离同一速度上的不同的角度则需要大于2的接收天线。如下图所示，为N个天线对应N个2D-FFT矩阵，然后做Angle-FFT来解出不同物体对应的ω。

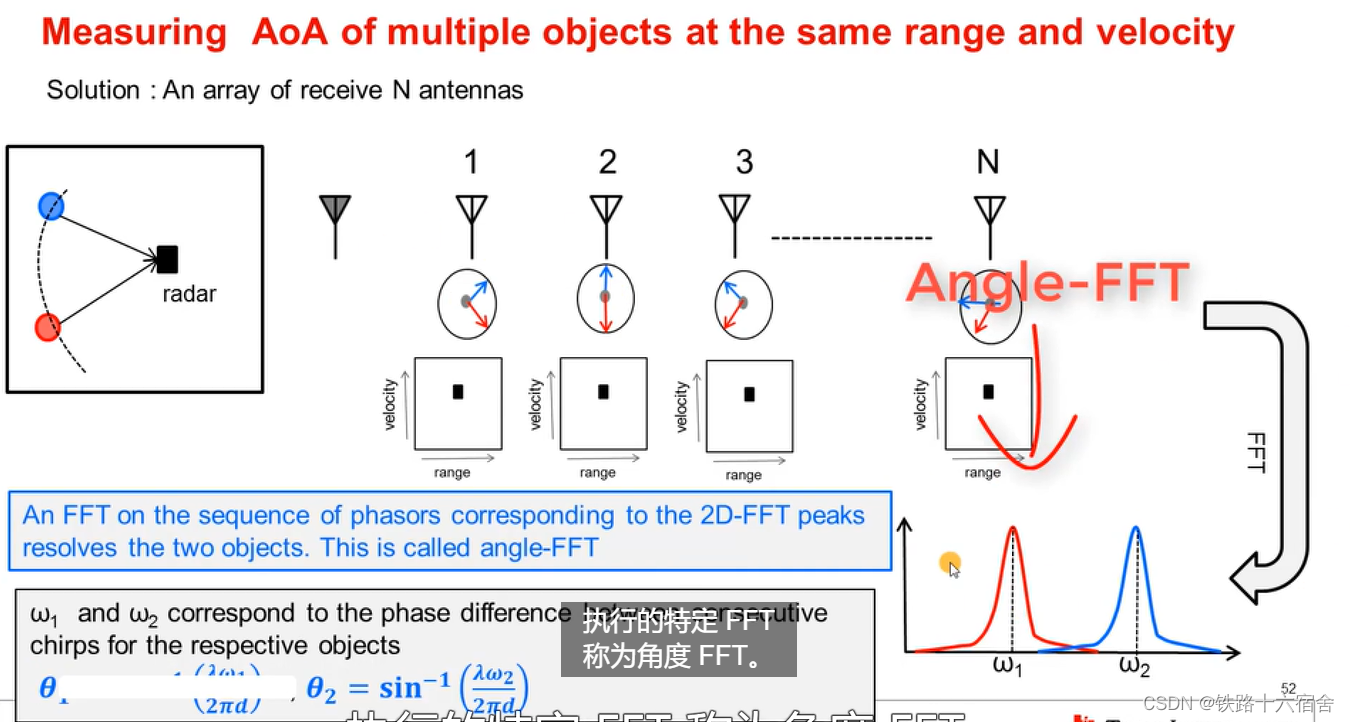
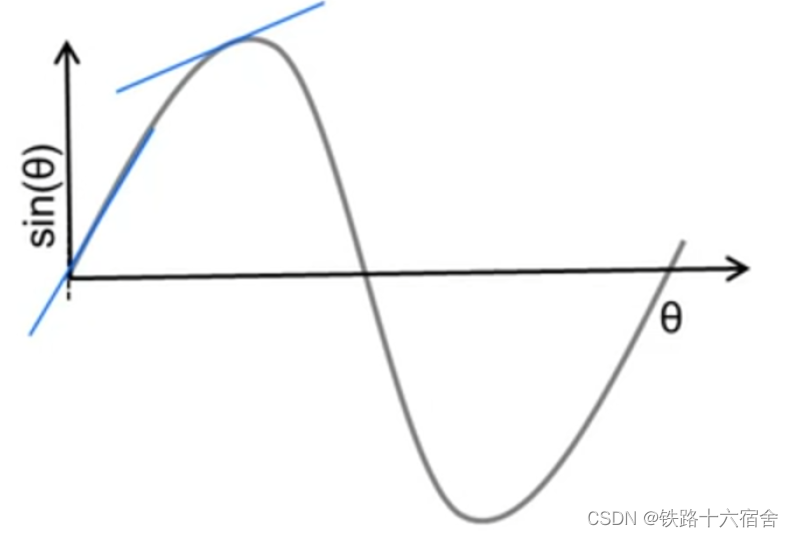
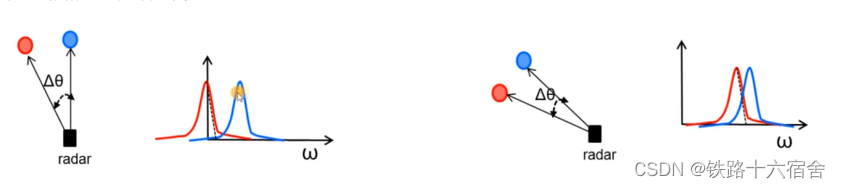
这里还有一个特性需要介绍一下，当物体在雷达正前方时，物体对雷达的角度测量效果十分好，但是当物体逐渐增加并且接近90°，当然由于噪声，估算角度的准确性会下降。 这是因为，根据公式$\omega =\frac{2\pi \Delta d}{\lambda }$，两个天线的对应谱峰的相位差和物体的雷达不是线性关系，ω和θ的关系如下图所示，在θ接近于0时，sin(θ)对θ十分的敏感，而θ接近90°时，sin(θ)对θ的变化非常不敏感。

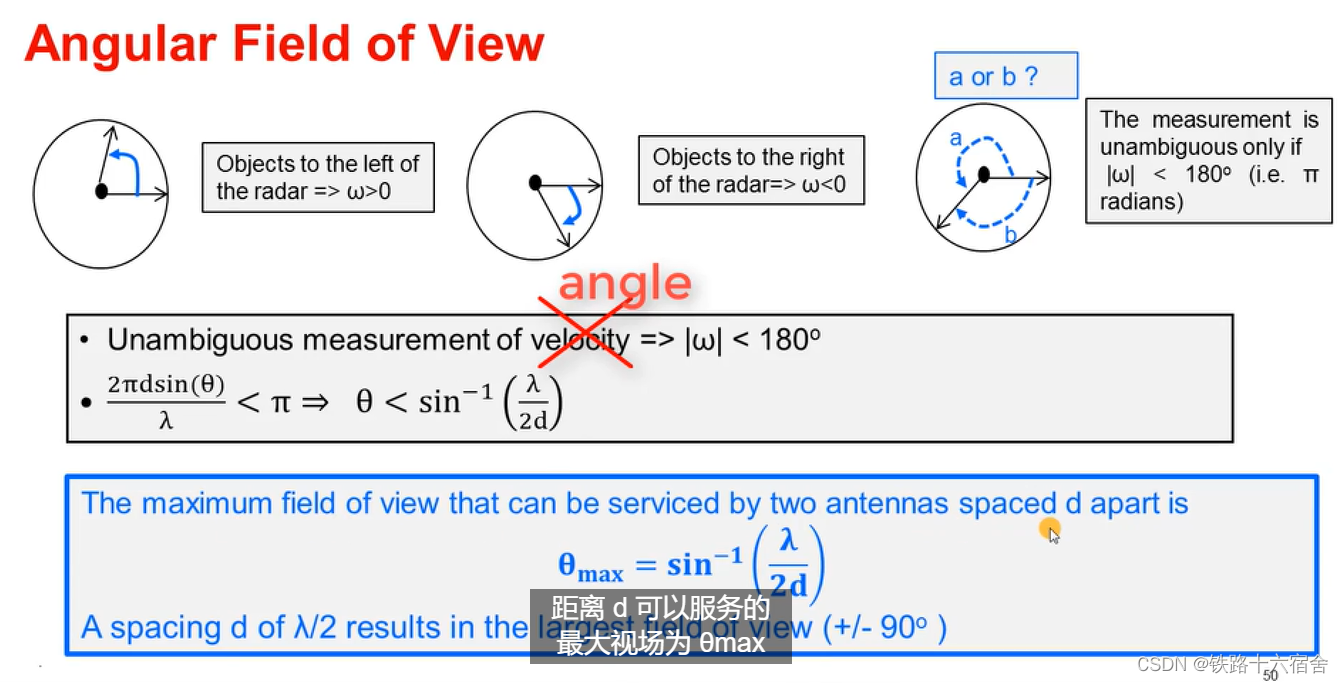
最大视场以及角度分辨率

当我们讨论速度估算时，我们看到雷达能够不模糊测量的速度具有上限。我们将此称为雷达的最大速度。雷达可以测量的最大不模糊角度是否存在类似的限制？，基本而言，速度的不模糊测量要求两个天线之间的相位变化小于 180 度。如下图所示，角度有类似的结论。我们看到雷达可以测量的最大角度必须小于λ 除以 2d 的反正弦，其中 d 是两个天线之间的距离。所以，我们可以得出最大视场，两个天线之间的距离 d 可以服务的最大视场为 ${\theta }_{max}$等于 λ 除以2d 的反正弦。请注意，在两个天线之间的距离如果为λ 除以2，可导致最大的可能视场正 90 度或负 90 度。

角度分辨率的定义:两个物体的到达角分别位于θ和θ+Δθ，那么当两个物体的角度差差异多少时，可以将两个物体的角度在角度FFT的谱峰中区分的出来，这就是角度分辨率的定义。
假设到达角θ为的物体具有离散频率ω，它为$\frac{2\pi dsin(\theta )}{\lambda }$，又因为FFT区分ω需要满足$\omega >\frac{2\pi }{N}$，N为FFT中的采样的样本数，所以我们可以进行如下的推导。

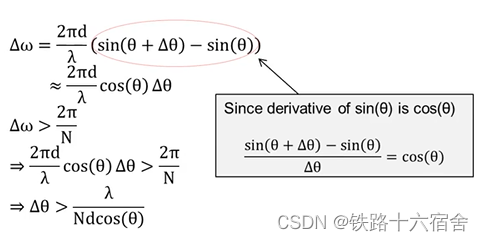
其中N是天线的数量，d是两个连续天线之间的距离，所以在上面的推导的公式可以得到${\theta }_{res}=(\frac{\lambda }{Ndcos(\theta )})$，通常假设两个天线之间的距离为 λ 除以 2，并且 θ 为 0，则公式变为${\theta }_{res}=(\frac{2}{N})$。,需要注意的一点是，这里的单位是弧度制。
如果您看看该表达式，有一点很有意思，即分辨率角度取决于 θ。这在距离或速度背景中未出现过。因此距离和速度分辨率都独立于实际的距离和速度值。其原因还是在于 sin(θ) 的不一致特性。因此，对于由 Δθ分隔的两个物体，其在角度 FFT 中的角频率在 θ 等于0 时实际上离得更远，并且随着 θ 的增大彼此越来越靠近，即使在两种情况下距离Δθ 相同也是如此。

正如您现在可能已经了解的那样，FMCW 雷达中的角度估算和速度估算取决于非常类似的概念。实际上，数学基础几乎是相同的。因此，我认为通过下图来比较这两者应该有所帮助。详细的对比关系在下图均已说明，这里不再赘述了。

最后，我们在完整的回顾一下角度估计的流程。首先，您具有合成器synth，也称为 LO 或本机振荡器，它可以生成线性调频脉冲。线性调频脉冲由发射天线进行发射。它从雷达前方的物体上进行反射。在每个接收天线处接收反射信号。synth 信号路由到其中的每个 RX天线，接收到的信号与 synth 信号混合，以创建 IF 信号。IF 信号经过低通滤波器，并由 ADC 进行采样。该ADC 数据在整个帧发生中进行处理，以创建一个 2D-FFT 网格，针对每个 RX 天线创建一个此类 2D-FFT 网格。该 2D-FFT 网格中的峰值与物体的距离和速度相对应。针对单一TX天线的所有RX天线的2D-FFT 中对应峰值进行的FFT称为角度 FFT，该角度 FFT中的峰值直接对应于物体的到达角。