目录
- 背景
- 思路与核心代码
- 数值实验
- 优缺点分析
- 参考文献
背景
在前面2文,我们分别讨论了利用夹角余弦来计算轨迹相似度和利用缓冲原理来计算轨迹相似度两种方法,前者可以作为一个baseline提供参考,后者的计算更符合人们的感官和事实,今天,我们要从计算机视觉出发,考察两条轨迹的相似度。
思路与核心代码
可以这么去想,首先,分别将两条轨迹点“串点连线”画出两条轨迹,同时控制画布的大小和渲染颜色,比如都是400*400像素的画布和轨迹都是黑色线段串连,其余都是白色的,如下图所示,
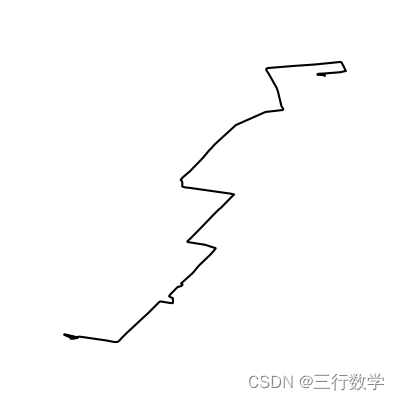 图1 轨迹1 图1 轨迹1
|
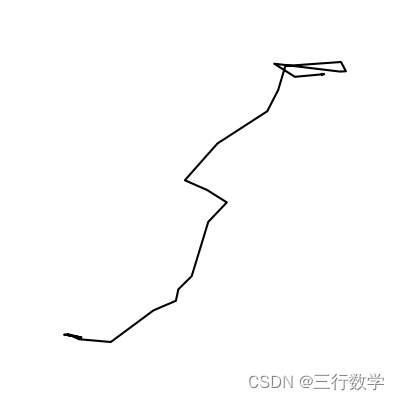 图2 轨迹2 图2 轨迹2
|
这样比较两条轨迹的相似度就转化为比较两张图片的相似度,而在计算机视觉领域,就有很多方法来比较两张图片相似度,这里采用图像切割法。图像切割法也比较好理解,就是用同样大小的网格去按照同样的方式去切割这两张图片,将图片分成相同数目的子图,相当于建立了一个网格坐标系,轨迹1的子图和轨迹2的子图在位置上可以建立起一一对应关系,也就是他们在网格坐标的位置一一对应,如果切割出来的位于网格坐标相同位置的某个子图恰好有轨迹1的一部分,又有轨迹2的一部分,那么就可以认为这个子图是这两条轨迹共同经过的区域,可以设计出一个Kronecker函数,对于任意的相同坐标相同尺寸的2个子图 i m g i img_i imgi和 i m g i ′ img_i' imgi′
K
(
i
m
g
i
,
i
m
g
i
′
)
=
{
1
,
i
m
g
i
∩
i
m
g
i
′
≠
∅
0
,
i
m
g
i
∩
i
m
g
i
′
=
∅
K(img_i, img_i')=\left\{ \begin{aligned} 1 & , img_i \cap img_i' \neq \emptyset\\ 0 &, img_i \cap img_i' = \emptyset \end{aligned} \right.
K(imgi,imgi′)={10,imgi∩imgi′=∅,imgi∩imgi′=∅
其中,
i
m
g
i
img_i
imgi表示轨迹1的第i个子图,
i
m
g
i
′
img_i'
imgi′表示轨迹2的第i个子图。然后,去统计轨迹1经过多少个子图,轨迹2经过多少个子图,其中,轨迹1和轨迹2共同经过的子图有多少个,从而就能计算出这两条轨迹的相似度了。
def trajectoryLine(trajectory, fig_name, grid_num): #轨迹连线绘图并网络切割
fig = plt.figure(figsize= (4, 4)) #dpi=300
ax = plt.subplot(111)
ax.plot(trajectory['lng'], trajectory['lat'], color = 'k') #轨迹图, marker ='.', color = 'k', linewidth = 0.0002
ax.set_axis_off()
plt.savefig(r"D:\钢联物流\中交轨迹与手机轨迹相似度\图片\{}.png".format(fig_name)) #保存本地
buffer_ = io.BytesIO() #开辟新的缓存
plt.savefig(buffer_, format = 'png')
buffer_.seek(0)
image = Image.open(buffer_)
image_parts = [] #用来存放切割后的局部图片PIL.Image.Image
weight = int(image.size[0] // grid_num)
height = int(image.size[1] // grid_num)
for j in range(grid_num):
for i in range(grid_num):
box = (weight * i, height * j, weight * (i + 1), height * (j + 1))
part = image.crop(box)
image_parts.append(part)
buffer_.close() #释放缓存
return image_parts
def whetherBlank(image): #判断一张图片是否纯白,如果是返回0,反之,返回1
# image_array = np.int8(image)
if np.mean(image)==255: #纯白
result = 0
else:
result = 1
return result
def cvSimilarity(traj1, traj2): #两个轨迹绘制并网格切分
traj1_parts = trajectoryLine(traj1, "traj1_line", grid_num = 40)
traj2_parts = trajectoryLine(traj2, "traj2_line", grid_num = 40)
traj1_list = [whetherBlank(part) for part in traj1_parts]
traj2_list = [whetherBlank(part) for part in traj2_parts]
print(len(traj1_list))
intersection_cnt = 0
for i in range(len(traj1_list)):
if traj1_list[i]==1 and traj2_list[i]==1:
intersection_cnt +=1
cv_sim_value = intersection_cnt/(np.sum(traj1_list)+np.sum(traj2_list)-intersection_cnt)
print(intersection_cnt, np.sum(traj1_list), np.sum(traj2_list))
print("网格相似度", cv_sim_value)
return cv_sim_value
数值实验
下面是对不同运单计算出来的相似度对比,整体还不错,前者是基于缓冲的相似度,后者是图像切割相似度,两者具有高度的一致性,但是在相似度高的轨迹,图像切割法会更高,在相似度本来就很低的对比情况下,图像切割法也会略微高出一些。
trajectory
优缺点分析
1,图像切割法直观形象好理解;
2,操作简便,无需做过多的考虑;
3,未考虑小图中各自轨迹点的密集程度的对相似度的影响;
4,网眼尺寸不好把握,其实也可以像缓冲相似度那样设计一个toleranceTest来决定网眼大小,也可以当作一个超参数,设计一个metric来进行调优。
参考文献
1,计算机视觉 - 图像相似度
https://blog.51cto.com/u_15668366/5412298
2,轨迹路线相似度计算
https://blog.csdn.net/weixin_39459401/article/details/129157653
3,Python-Opencv中用compareHist函数进行直方图比较进行对比图片
https://blog.csdn.net/qq_44262417/article/details/89217011
4,计算两幅图像的相似度(PSNR、SSIM、MSE、余弦相似度、MD5、直方图、互信息、Hash)& 代码实现 与举例
https://blog.csdn.net/m0_61899108/article/details/127715737