一、定义
二叉树可以用以下方式详细定义：
- 二叉树是由节点构成的树形结构，每个节点最多可以有两个子节点。
- 每个节点有以下几个属性：
- 值：存储该节点的数据。
- 左子节点：有一个左子节点，如果没有则为空。
- 右子节点：有一个右子节点，如果没有则为空。
- 父节点：有一个父节点，如果没有则为空（除根节点外）。
- 根节点：二叉树的顶部节点，没有父节点。
- 叶子节点：没有子节点的节点，也称为终端节点。
- 子树：以某个节点作为根节点的二叉树称为它的子树。
- 遍历：二叉树的节点遍历可以分为前序遍历、中序遍历和后序遍历，还有层次遍历。
注意：二叉树中的节点数量可以为0，1或多个，空的二叉树也是一棵有效的二叉树。
二、几种特殊的二叉树
1、满二叉树，一个高度为h含有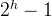
个结点的二叉树
特点：
1.只有最后一层有叶子结点。
2.不存在度为1的结点。
3.按层序从1开始编号，结点i的左孩子为2i，右孩子为2i+1，父结点为。
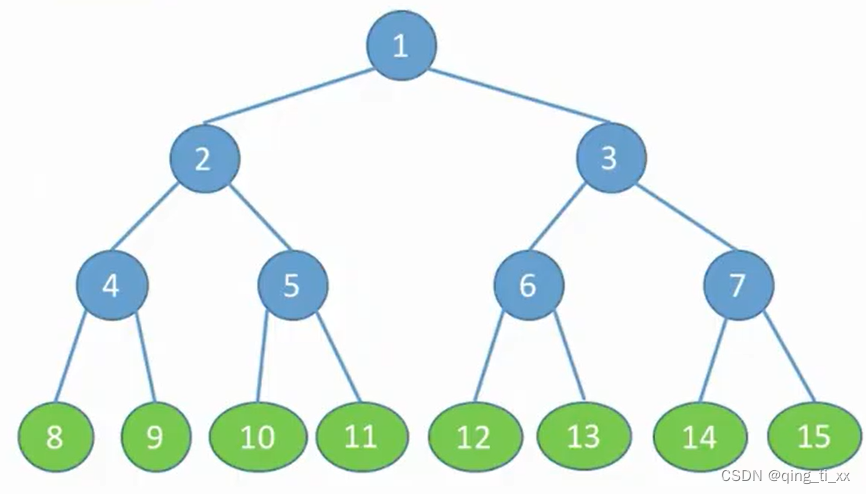
2、完全二叉树，与同高的满二叉树的子节点编号一致
此图的4层的编号与上图的第4层一一对应，称之为完全二叉树。
特点：
1.只有最后两层有叶子结点。
2.最多存在一个度为1的结点。
3.按层序从1开始编号，结点i的左孩子为2i，右孩子为2i+1，父结点为。
4.i<=为分支结点，i>=
为叶子节点。
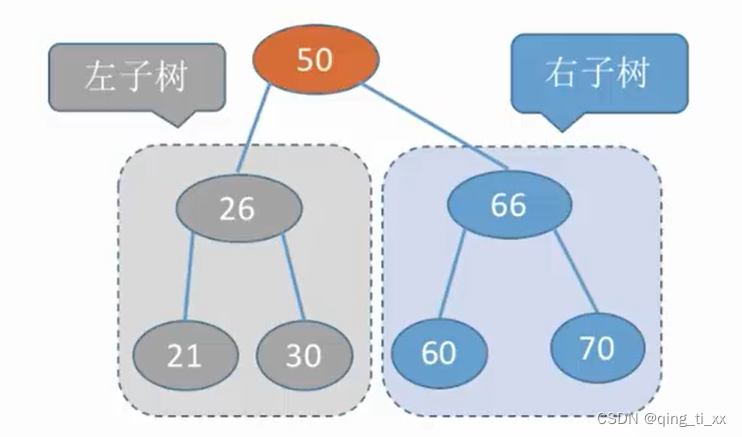
3.二叉排序树
一棵二叉树或者是空二叉树，或者是具有如下性质的二叉树:
左子树上所有结点的关键字均小于根结点的关键字;
右子树上所有结点的关键字均大于根结点的关键字。
左子树和右子树又各是一棵二叉排序树。
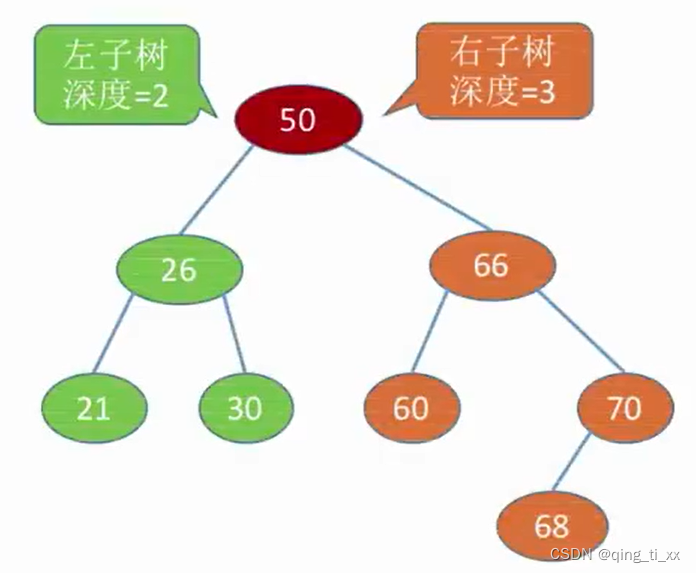
4.平衡二叉树，树上任一结点的左子树和右子树的深度之差不超过1
三、考点
常见考点1:
设非空二叉树中度为0、1和2的结点个数分别为n0、n1,和n2，则n0= n2+1
★★★★★(叶子结点比二分支结点多一个)
常见考点2:
二叉树第i层至多有个结点（ i≥1)
m叉树第i层至多有个结点（( i≥1)
常见考点3:
高度为h的二叉树至多有个结点（满二叉树)
常见考点4:
具有n个(n>0）结点的完全二叉树的高度h为或
常见考点5：
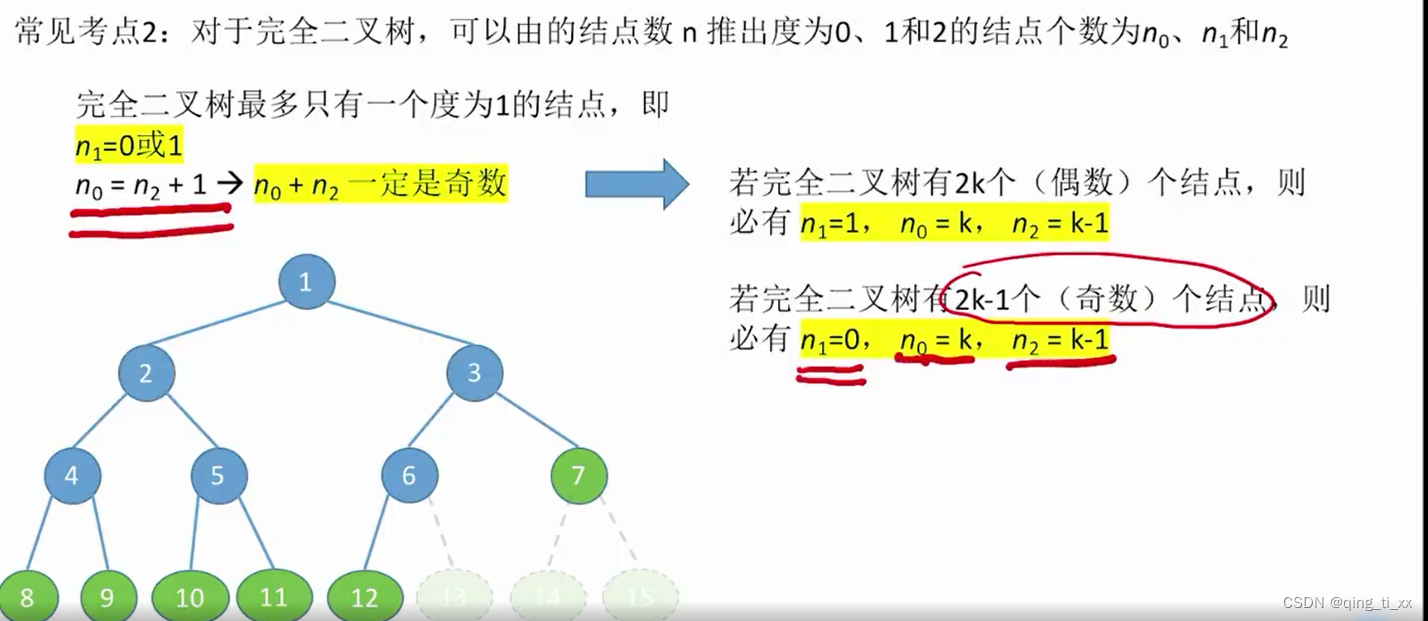
四、WPL算法
我们使用先序遍历求WPL
1.先定义二叉树；
2.定义一个递归函数，当当前结点为叶结点时，累计wpl的值
3.若左节点不为空，将左孩子作为新的根结点，深度加一，开启新一轮的递归。
4.若右节点不为空，将右孩子作为新的根结点，深度加一，开启新一轮的递归。
5.当所有子树都遍历到叶节点后结束递归，返回wpl；
#include "stdlib.h"
typedef struct BiNode{
int weight;
struct BiNode *lchild,*rchild;
}BiTNode,*BiTree;
int wpl_PreOrder(BiTree root, int deep){
static int wpl=0;
if (root->rchild==NULL && root->lchild==NULL){
wpl+=deep*root->weight;
}
if (root->lchild!=NULL){
wpl_PreOrder(root->lchild,deep+1);
}
if (root->rchild!=NULL){
wpl_PreOrder(root->rchild,deep+1);
}
return wpl;
}
int WPL(BiTree root){
return wpl_PreOrder(root,0);
}
