完全平方数

news2025/1/19 17:22:52

题目链接

完全平方数

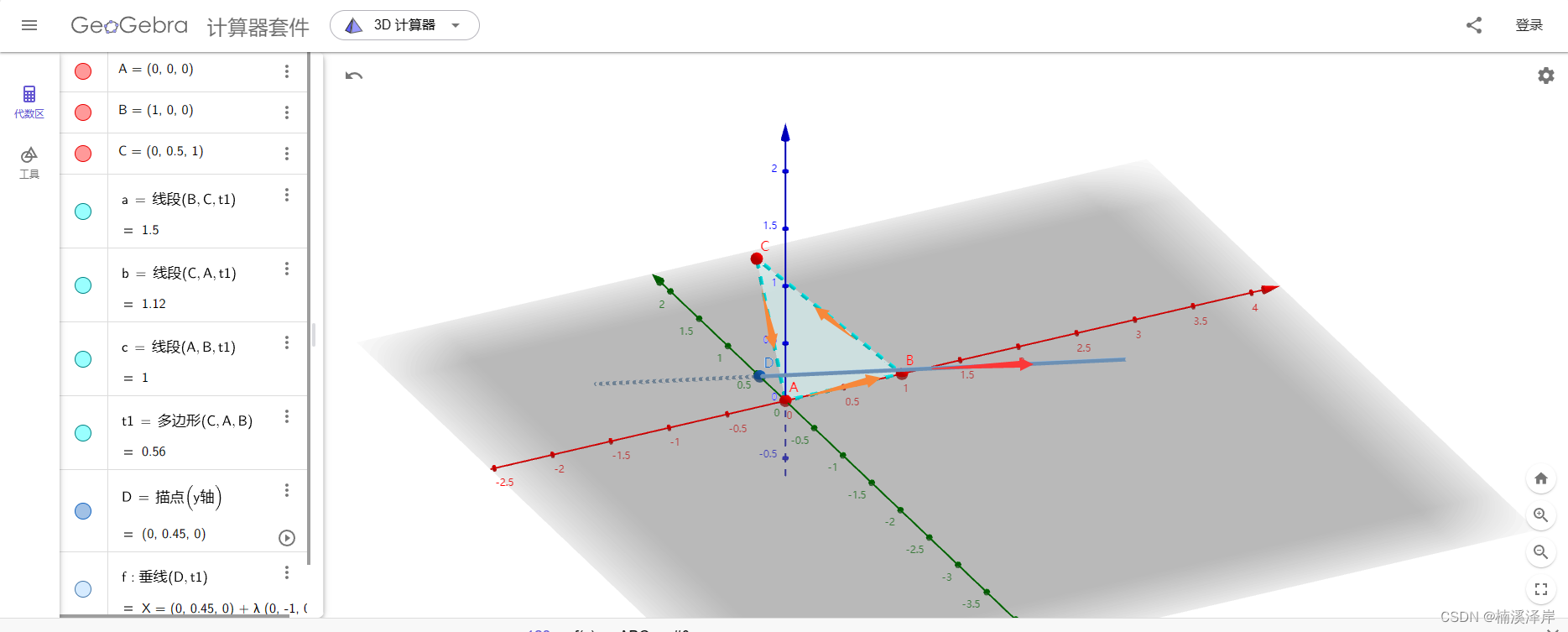
题目描述

注意点

返回和为 n 的完全平方数的最少数量

解答思路

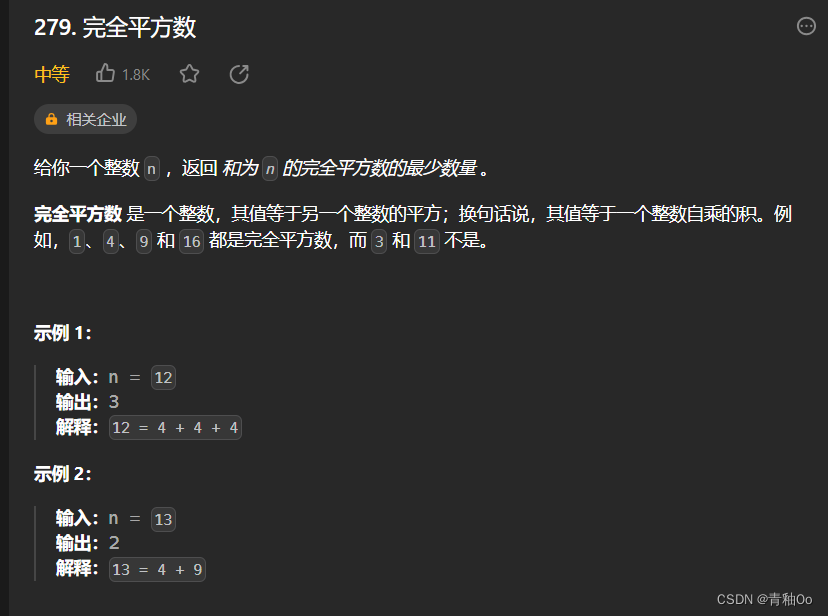
初始想到使用动态规划，后续数字的完全平方数可以由前面数字的完全平方数求得，对于任意数字，可以计算其减去从1…i之间（保证做减操作后的值大于等于0）的一个平方数，得到其前面数字的完全平方数，再加1个1…i之间的平方数就可求得该数字的完全平方数，公式如下：
f(n) = f(n - i²) + 1
还有一种数学方法可以以更快计算出结果，一个数学定理可以帮助解决本题：「四平方和定理」
四平方和定理证明了任意一个正整数都可以被表示为至多四个正整数的平方和。这给出了本题的答案的上界，最终结果只有4种，也就是1、2、3、4
当此时n可以直接表示为某个数i的平方，此时答案为1
当此时n减去某个数i的平方后的数字k可以直接表示为另一个数j的平方，公式为f(n) = f(n - i²) + 1，其中f(n - i²) = j²，此时答案为2
答案为3时，毕竟难以判断，可以通过排除另外三种情况得到答案3
四平方和定理包含了一个更强的结论：当且仅当n = Math.pow(4, k) * (8m + 7)时，n 只能被表示为四个正整数的平方和。此时答案为 4

代码

方法一：

// 动态规划
class Solution {
    public int numSquares(int n) {
        int[] dp = new int[n + 1];
        for (int i = 1; i <= n; i++) {
            int minNum = Integer.MAX_VALUE;
            int sqNum = 1;
            while (sqNum * sqNum <= i) {
                minNum = Math.min(minNum, dp[i - sqNum * sqNum] + 1);
                sqNum++;
            }
            dp[i] = minNum;
        }
        return dp[n];
    }
}

方法二：

// 数学方法
class Solution {
    public int numSquares(int n) {
        if (isPerfectSquare(n)) {
            return 1;
        }
        if (checkAnswer4(n)) {
            return 4;
        }
        for (int i = 1; i * i <= n; i++) {
            int j = n - i * i;
            if (isPerfectSquare(j)) {
                return 2;
            }
        }
        return 3;
    }

    // 判断是否为完全平方数
    public boolean isPerfectSquare(int x) {
        int y = (int) Math.sqrt(x);
        return y * y == x;
    }

    // 判断是否能表示为 4^k*(8m+7)
    public boolean checkAnswer4(int x) {
        while (x % 4 == 0) {
            x /= 4;
        }
        return x % 8 == 7;
    }
}