目录

题目：

示例：

分析：

代码：

---

题目：

示例：

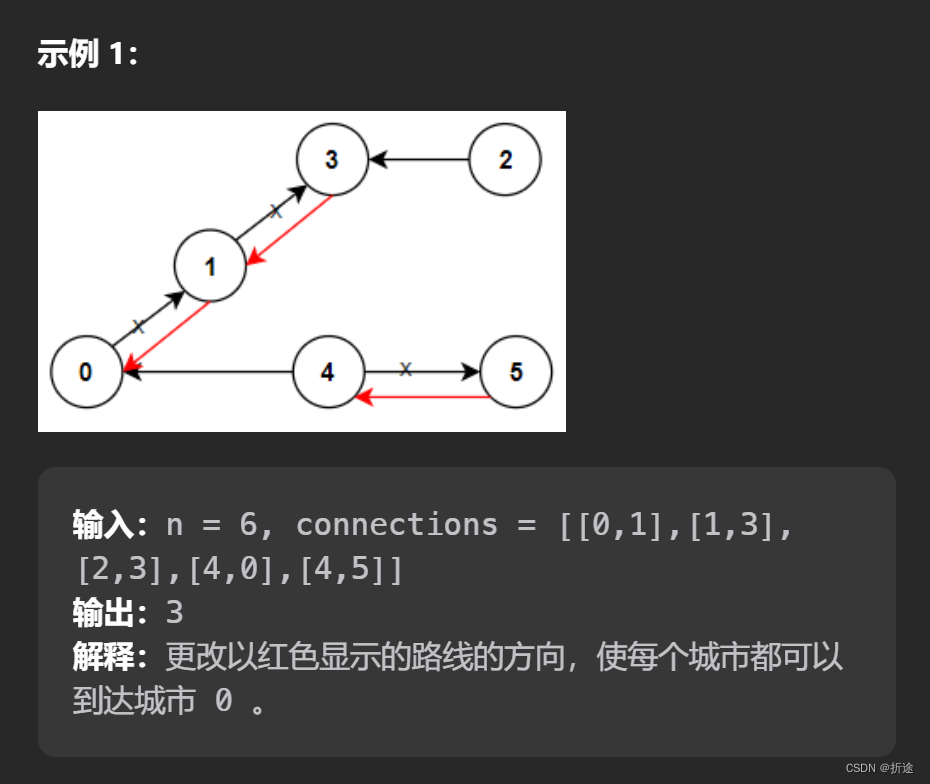
分析：

给我们一个表示城市连通情况的有向图，要求每个城市都要可以通向0号城市，不同城市之间只有一条路线，我们每次可以改变一条路线的指向，问我们需要操作多少次才可以达到每个城市都可以通向0号城市的要求。

由于不同城市之间只有一条路线，那么如果不看路线指向的话，将其看作是一个无向图，那么它就只是一棵树而已，而树的根节点就是0号城市，因为题目保证每个城市都能够在规划路线之后通往0号城市。

那么实际上我们可以通过根节点遍历到一棵树的每一个节点，并且路线是唯一的，所以我们可以当作遍历一棵树一样，通过遍历0号城市来通向每个城市，在发现节点之间的指向不对时，将操作次数加一，再遍历完所有城市之后，即可获取所有操作次数。

首先我们先构造图，一般构造图是用的map，不过这边的城市是连号的，那么直接用数组存放就可以了，下标就是对应的城市。

构造图是遍历城市的连接情况，只要两个城市的相连的，先不管方向，就在对应的位置加上对方城市，如果方向是走得到的就加个true的标记，如果是走不到的就加个false标记。

遍历完城市连接情况，图也就初步构建完毕。

接着我们从0号城市开始遍历，首先遍历和0号城市相邻的城市，这边要注意不走回头路，否则会死循环，所以dfs中需要记录一下当前城市的上一个城市，也就是该城市通往0号城市的路上的第一个城市。

遍历时我们看一下方向，如果方向是正确的，也就是向着0号城市的我们就不管，反之操作次数+1。接着再以此城市开始新一轮的DFS，直到遍历结束，我们将操作次数返回即可。

代码：

class Solution {
public:
    //int minReorder(int n, vector<vector<int>>& connections) {
    //     暴力超时
    //     vector<bool>can(n,false);
    //     can[0]=true;
    //     int res=0;
    //     int check=1;
    //     while(check!=n){
    //         for(vector<int>c:connections){
    //             if(can[c[0]]&&!can[c[1]]){
    //                 can[c[1]]=true;
    //                 reverse(c.begin(),c.end());
    //                 res++;
    //                 check++;
    //             }
    //             if(can[c[1]]&&!can[c[0]]){
    //                 can[c[0]]=true;
    //                 check++;
    //             }
    //         }
    //     }
    //     return res;
    // }
    int res=0;
    void build(int n, vector<vector<int>>& connections){    //构造图,将相邻的城市都联系起来
        for(auto &c:connections){
            graph[c[0]].push_back({c[1],true});
            graph[c[1]].push_back({c[0],false});
        }
    }
    void dfs(int cur,int pre){
        for(auto &c:graph[cur]){    //遍历与当前城市相连的城市    
            if(c.first!=pre){       //不走回头路
                if(c.second==true)  //如果是反方向,那么需要将其转个方向,res++
                    res++;
                dfs(c.first,cur);   //接着走下去
            }
        }
    }
    vector<vector<pair<int,bool>>>graph;
    int minReorder(int n, vector<vector<int>>& connections) {
        graph.resize(n,vector<pair<int,bool>>(0));
        build(n,connections);
        dfs(0,-1);
        return res;
    }
};