BBR 倾向于排空队列,甚至用特殊的 ProbeRTT 状态来排空自己产生的队列以测量 RTT,但这并不现实。一言以蔽之,BBR 无法实时跟踪现状,只靠拢理想。
若因背景流量造成 buffer 抖动,BBR 完全无法应对,其运行状态甚至非常糟糕。本文提一个自己的想法。用一个值而不是两个值逼近最优的收益成本比,而不是逼近 bltBW 和 RTprop。
BBR 给出了最佳效能操作点,在上周的文章中我导出了 E/inflt 曲线:

深入 E/inflt 曲线,我发现它比 maxB 和 minD 的乘积 BDP 更适合作不动点,理由如下:
- 队列虽并非自己所为,但始终存在。需求是收敛到 “最大的吞吐” 和 “最小的延时”,而不是排空排队。
- 端到端难控制全链路的 pacing rate,用 inflight 作控制更合适,pacing rate 只需大致吻合或取定值。
统计复用系统中,统计度量比精确控制更具实际意义,我经常质疑 BBR 参数取值的精确数学推导,相反,我赞成取经验值更合适。
端到端拥塞控制像足球一样不确定,没有谁且没有什么技术能保证一场比赛可以百分百进几个球,不确定性是足球观赏性之根,但即使这样还是有公认的强队,赢的就是统计概率。
我有一个新方法应对实际而非理想场景,其它流量排队的场景,BBR 依然可收敛到最佳操作点,正所谓要顺势而为。
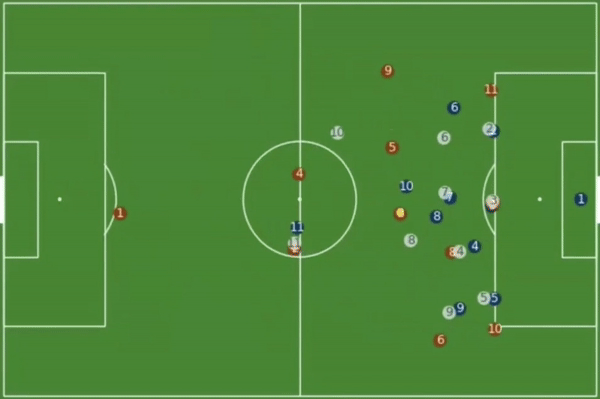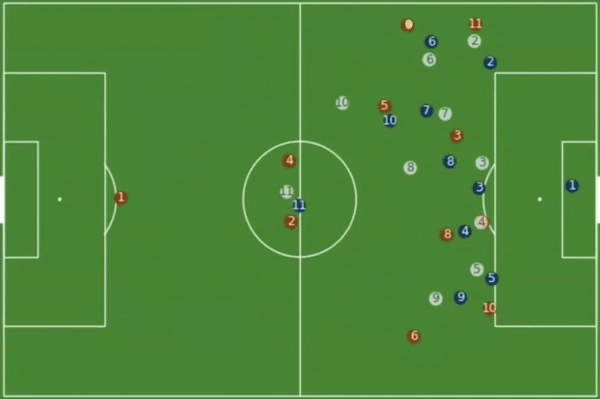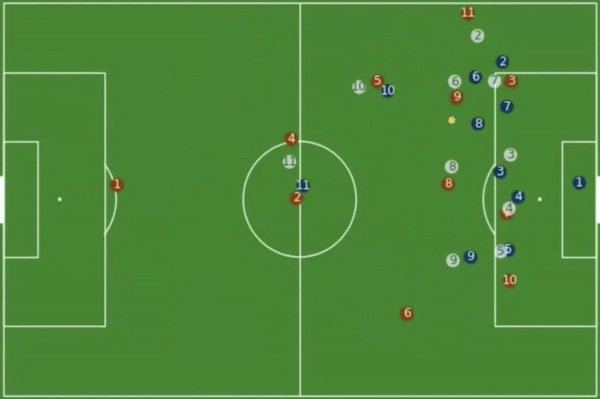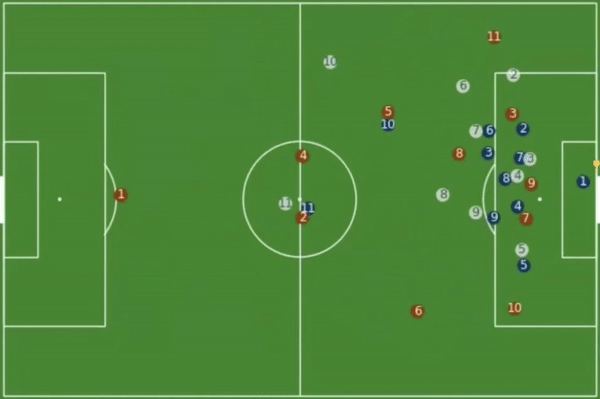
考虑以下左图多流场景下的 E/inflt 拉弗曲线,增加流数量维度,得到以下右图:
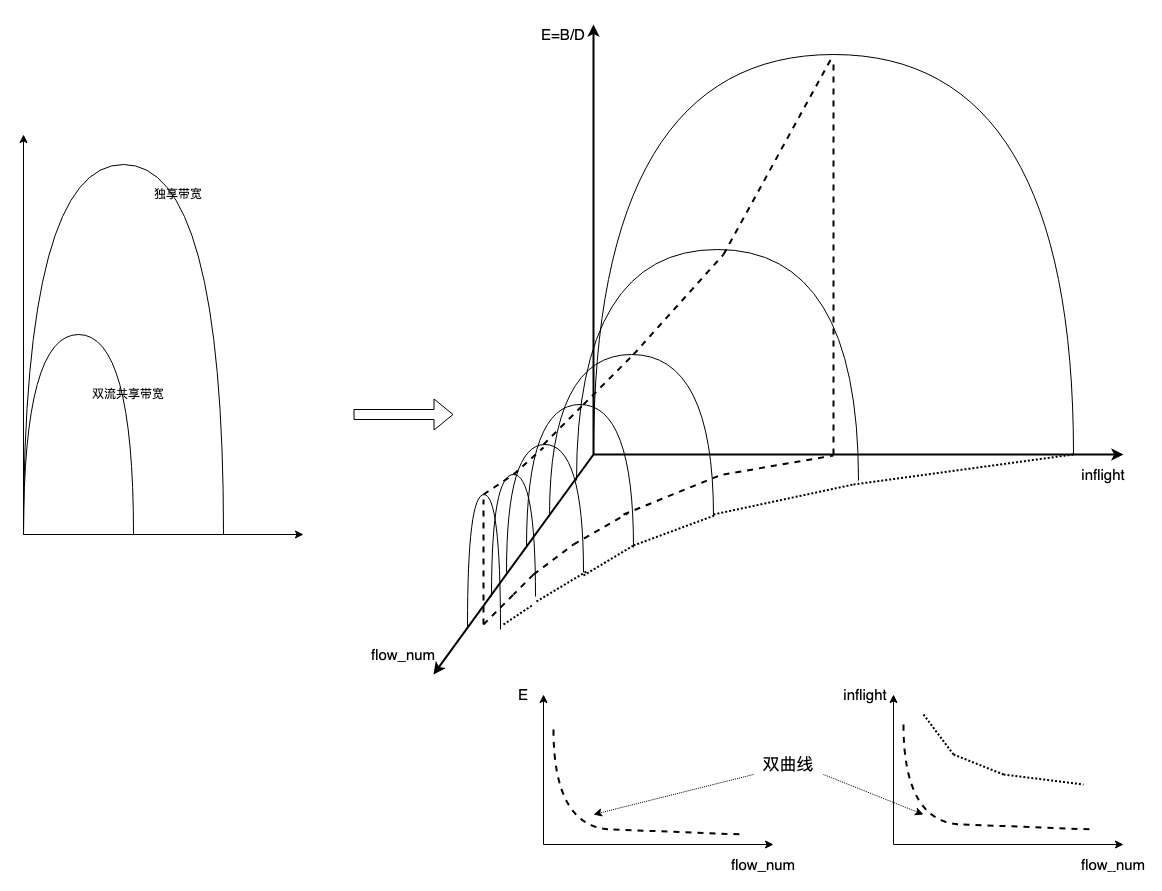
我用右下的两个小图解释了右上那个 “山脊” 的形状,山脊 “高度” 落差拟合双曲线,其投影在 “水平” 方向也拟合双曲线。
双曲线很容易理解,E = B/D,若 2 流共享带宽,全局最佳效能依然是不排队,E = 1/2B/D + 1/2B/D,若 3 流,每条流的 B 则为 1/3,以此类推,1/4,1/5,即 y = 1/N,为双曲线,同理,每条流达到最佳 E 的 inflt 亦为 1/N 的关系,为双曲线。
自然界很少见这形态的物件儿,我用拟合了一个曲面,随便看看:
z
=
−
y
(
x
−
1
y
)
2
+
1
y
z=−y(x−\dfrac{1}{y})2+\dfrac{1}{y}
z=−y(x−y1)2+y1

换个角度:

BBR 的整个运行过程应是 “通过调整 x, 在 ‘等 y 线’ 上不断爬到山脊“:
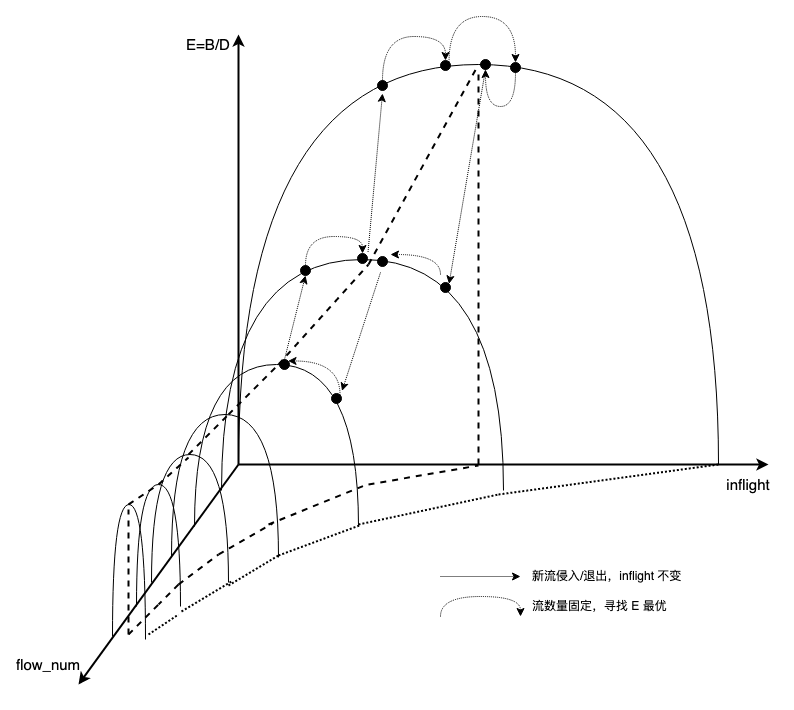
于是,YaBBR 算法即:
- 第 1 步,增加 cwnd,测量 E = B/D,直到由增到减的转变,找到 “顶点”。
- E = B/D 减小,减小 cwnd,测量 E = B/D 直到开始增加,重复 1。
- E = B/D 增大,重复 1。
至于公平性,与标准 BBR 无异,可通过类似 ProbeRTT 的主动排空过程收敛到公平,也可以 ProbeBW 中挤占吞吐与加速比的负相关关系收敛到公平。二者效果一致,一个排空,一个探测,方向不同而已。
BBR 直到 v2 仍是基于理想模型修补,很难适应现实场景。几乎不可能不产生队列,一旦产生队列,Startup 退出条件基本就是奢望,只要 buffer 不满,吞吐总是能挤兑出来,这非常不利于公平性,而一旦 buffer 溢出,一切又为时已晚。BBR 的最大带宽假设本就不成立,最小 RTT 也几乎很难算数。况且 10secs 的最小 RTT 保质期完全不能保证。总之,BBR 假设一个理想环境,且独享带宽,方可实现,其它的都是后来加进去的。因此,需要一个新的思路,寻找一个新的不动点作为 BBR 的操作点。本文简单描述一个思路,称为 YaBBR
浙江温州皮鞋湿,下雨进水不会胖。