说在前面
今天给大家带来B树系列数据结构的讲解！
博主为了这篇博客，做了很多准备，试了很多画图软件，就是为了让大家看得明白！希望大家不要吝啬一键三连啊！！
前言
那么这里博主先安利一下一些干货满满的专栏啦！
手撕数据结构
https://blog.csdn.net/yu_cblog/category_11490888.html?spm=1001.2014.3001.5482算法专栏https://blog.csdn.net/yu_cblog/category_11464817.html
STL源码剖析
https://blog.csdn.net/yu_cblog/category_11983210.html?spm=1001.2014.3001.5482
为什么我们需要B树
目前学习了这么多数据结构，我们可以了解到的搜索结构如下表所示：
| 种类 | 数据格式 | 时间复杂度 |
|---|---|---|
| 顺序查找 | 无要求 | O(n) |
| 二分查找 | 有序 | O(logn) |
| 二叉搜索树 | 无要求 | O(logn) 最坏:O(n) |
| 二叉平衡搜索树 | 无要求 | O(logn) |
| 哈希 | 无要求 | O(1) |
以上结构适合用于数据量相对不是很大，能够一次性存放在内存中，进行数据查找的场景。如果
数据量很大，比如有100G数据，无法一次放进内存中，那就只能放在磁盘上了，如果放在磁盘
上，有需要搜索某些数据，那么如果处理呢？那么我们可以考虑将存放关键字及其映射的数据的
地址放到一个内存中的搜索树的节点中，那么要访问数据时，先取这个地址去磁盘访问数据。
例子：
假设我们用一棵二叉平衡搜索树存储10亿个数据。由于数据太多太大（key太大），我们内存中是存不下的，因此我们节点里面存的是数据在磁盘中的地址。由于我们在查找一个数的时候，是需要对比的，但是我们的key值其实没有存储在内存中，因为我们需要进行一次IO，到磁盘中，我们才能完成对比。10亿个数据，即30层左右的平衡树。
如果我们查找一个数字，需要30次IO，这个时间消耗是巨大的！现在我们认为，同样是10亿个数据，我只想进行2~3次IO，怎么办？我们需要压缩高度！
如何压缩搜索树的高度？
- 二叉变多叉
- 一个节点存多个key的地址
B树概念
一棵m阶(m>2)的B树，是一棵平衡的M路平衡搜索树，可以是空树或者满足一下性质：
- 根节点至少有两个孩子
- 每个分支节点都包含k-1个关键字和k个孩子，其中 ceil(m/2) ≤ k ≤ m （ceil是向上取整函数）
- 每个叶子节点都包含k-1个关键字，其中 ceil(m/2) ≤ k ≤ m
- 所有的叶子节点都在同一层
- 每个节点中的关键字从小到大排列，节点当中k-1个元素正好是k个孩子包含的元素的值域划分
- 每个结点的结构为：（n，A0，K1，A1，K2，A2，… ，Kn，An）其中，Ki(1≤i≤n)为关键字，且Ki<Ki+1(1≤i≤n-1)。Ai(0≤i≤n)为指向子树根结点的指针。且Ai所指子树所有结点中的关键字均小于Ki+1。n为结点中关键字的个数，满足ceil(m/2)-1≤n≤m-1。
其实我们熟知的二三查找树，就是一棵三阶的B树。虽然我们今天重点要学习的是B树，但是其实在日常使用中，B+树才是最常用的。
当然光看文字，我们肯定是比较难以理解的，因此，博主将用插入的形式，慢慢给大家解释上面的规则。
B树的插入
B树的插入的核心，就是节点的分裂。
注意：插入节点一定是在叶子上插入！为什么？请看下面详细插入过程。
下面我们用序列[53,139,75,49,145,36,50,47,101]来给大家进行解释。（设B树阶数 M == 3）
- 插入节点53
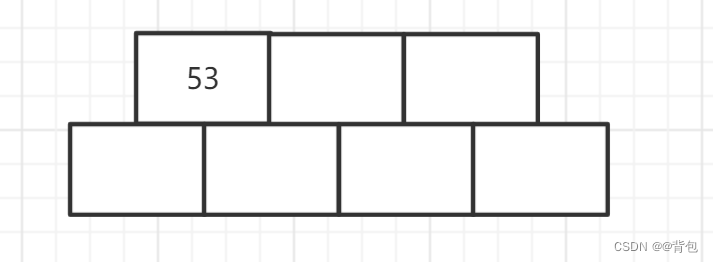
由于在一个节点中，孩子比关键字的数量多一个，所以上述结构我们就可以很好的理解了。
此时，M==3，而我们却画了4个孩子的空间，这是为什么？这其实是为了简化我们在实现B树分裂过程的代码，这里我们就先保留这个疑问，等博主介绍完插入，我们自然就明白了！
- 插入节点139
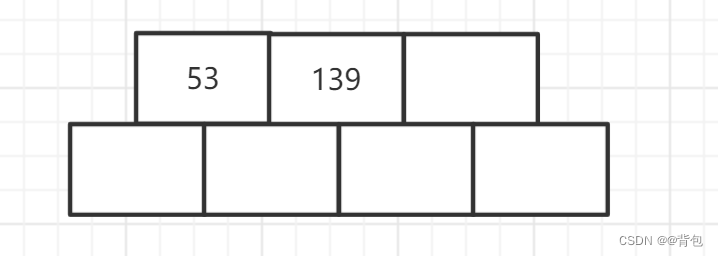
由于性质5，所以我们在每一个节点中，key值都是递增的，所以139插入到53的后面。此时我们还是满足B树的性质的，一个节点并没有满。因此当前阶段，我们不需要分裂。
- 插入节点75
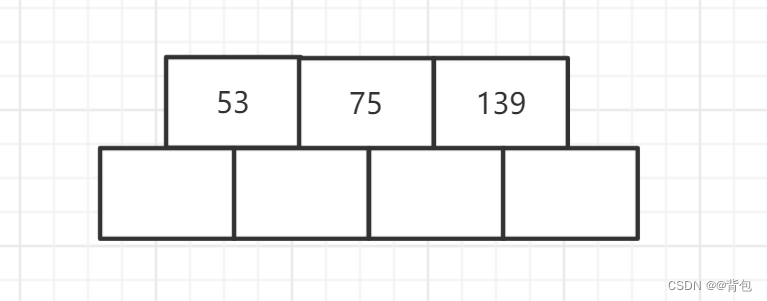
插入75之后，我们发现，key的数量已经超过了规定的最大数量（3-1=2个），因此，此时我们要进行分裂。
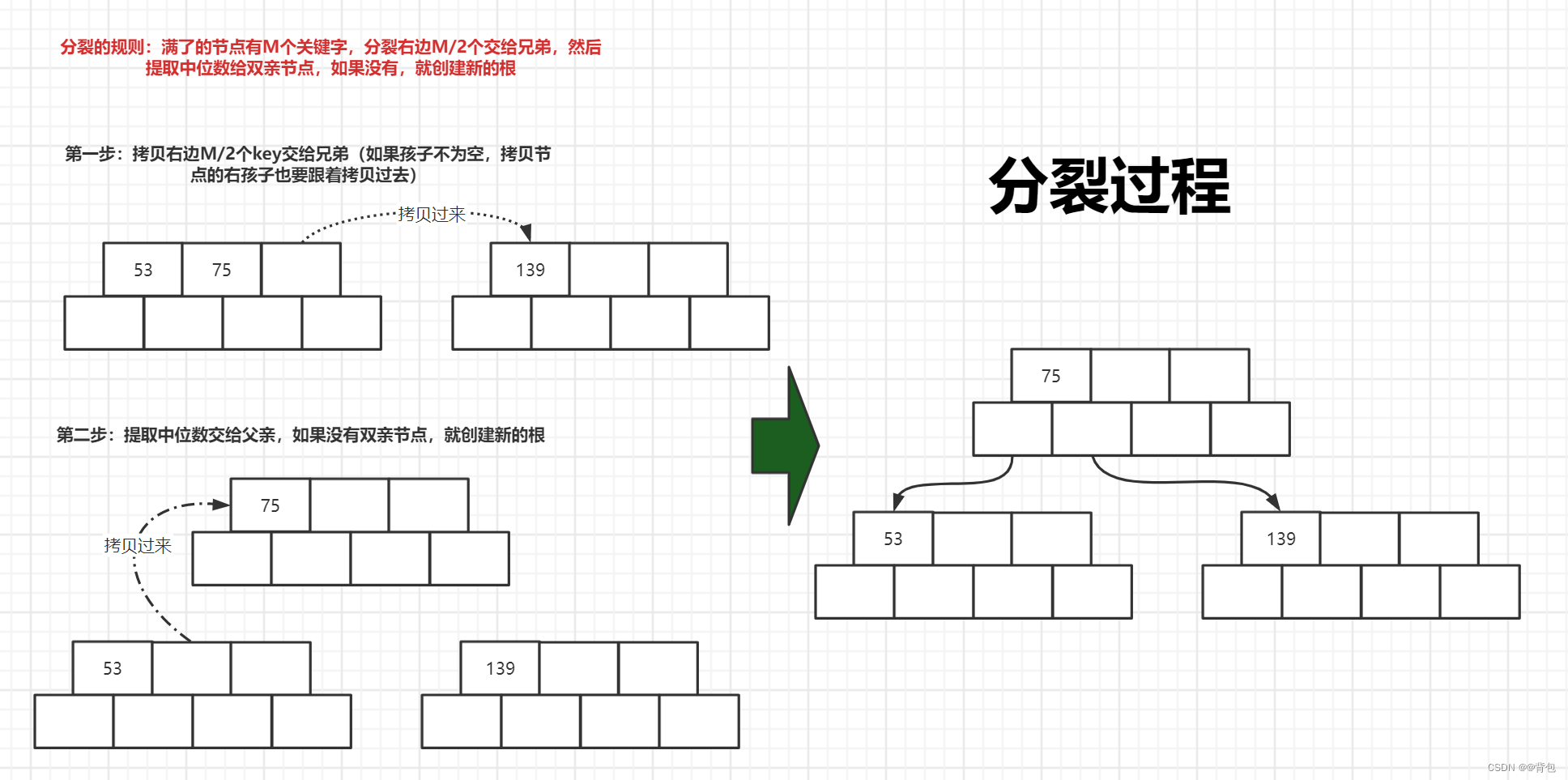
此时我们已经可以发现，为什么我们要多开一个key和孩子的节点位置。因为这样，我们可以先把节点插入进来，再判断节点是否满，是否需要分裂。如果不开多一个位置，我们都不知道怎么去分裂了，因为一插入就越界了。
- 插入节点49
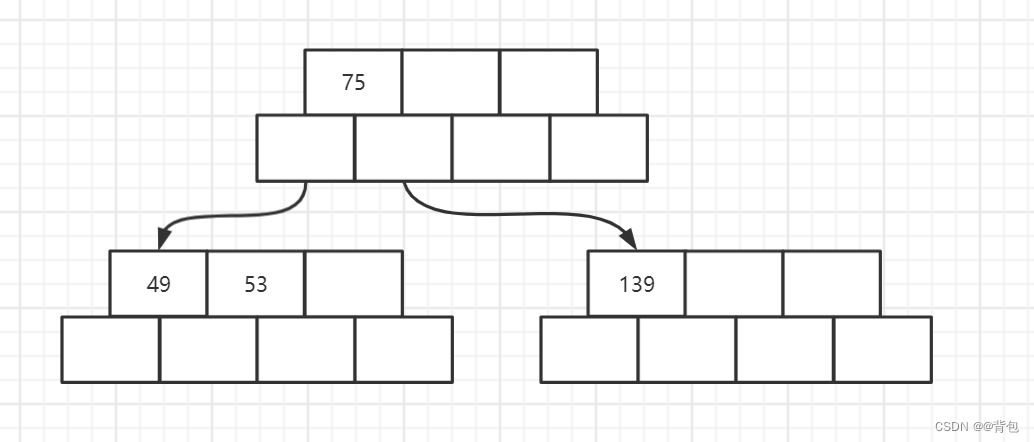
- 插入节点145
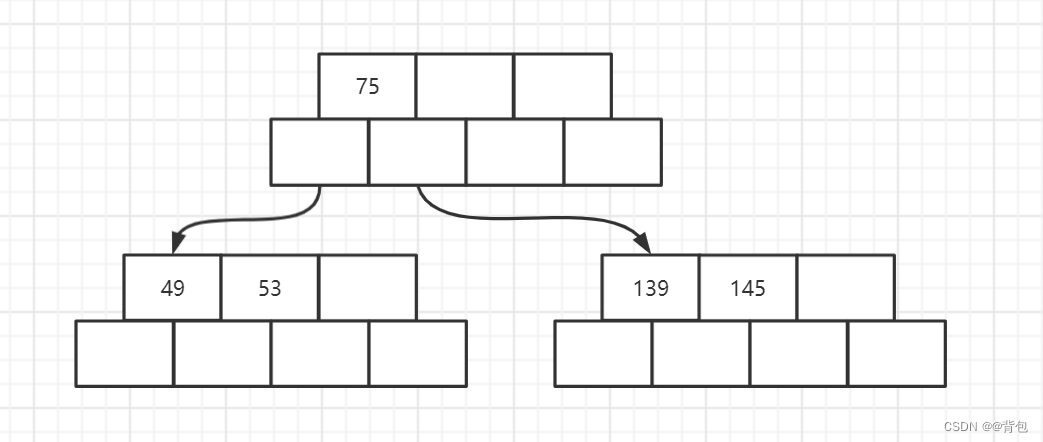
- 插入节点36
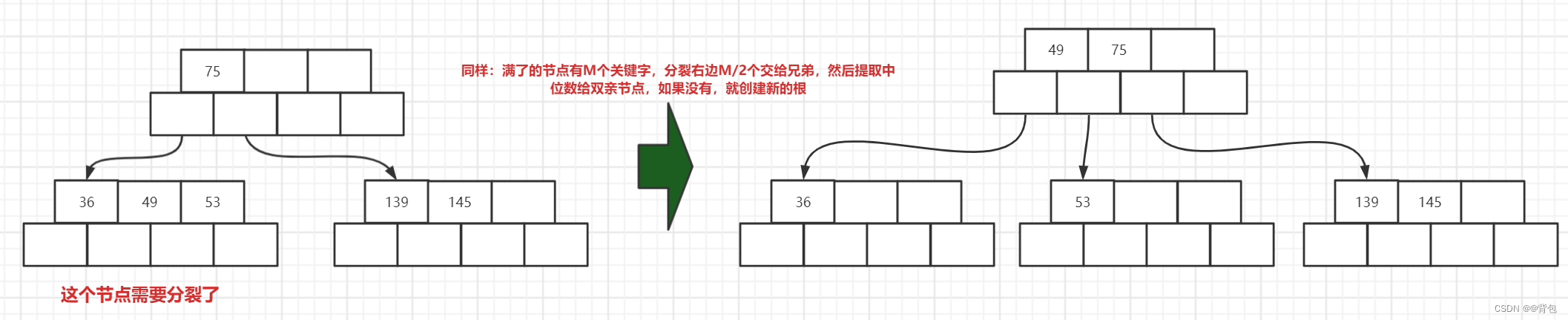
插入36之后，我们发现我们需要分裂了，因此像刚刚一样，完成一次分裂即可。
- 插入节点101
此时是一个连续分裂的过程
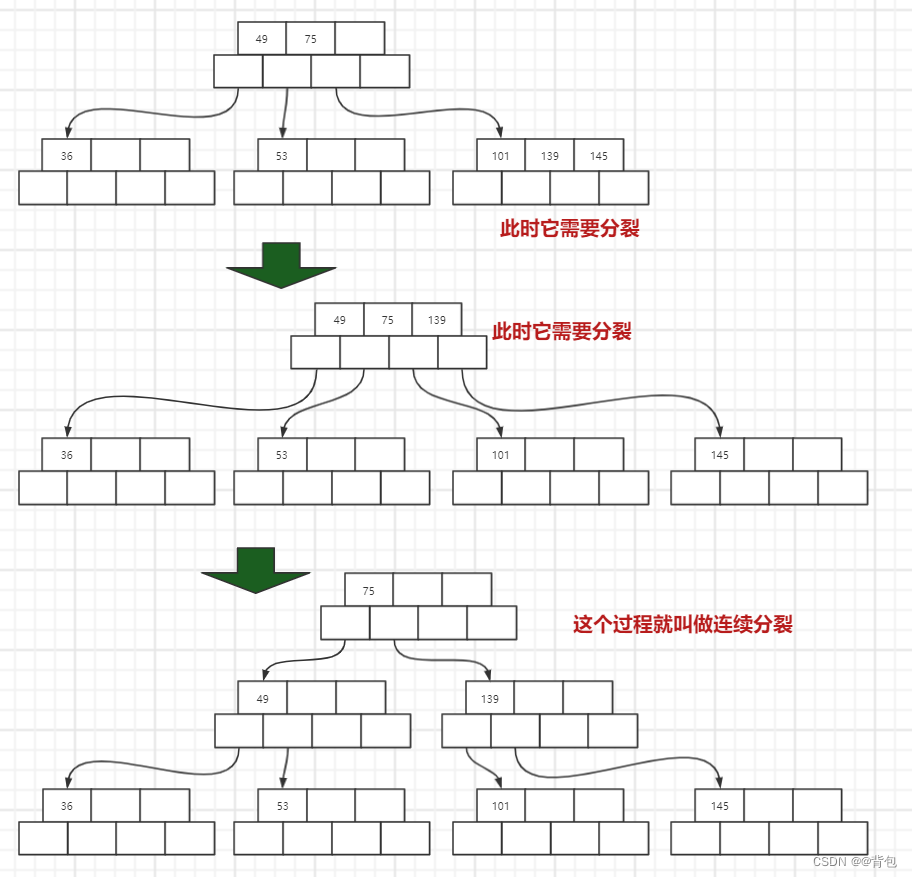
看到这里，相信大家已经对B树是如何完成插入，有了一定的了解了，接下来我们来做一个做一个总结。
插入过程总结：
- 如果树为空，直接插入新节点中，该节点为树的根节点
- 树非空，找待插入元素在树中的插入位置(注意：找到的插入节点位置一定在叶子节点中)
- 检测是否找到插入位置(假设树中的key唯一，即该元素已经存在时则不插入)
- 按照插入排序的思想将该元素插入到找到的节点中
- 检测该节点是否满足B-树的性质：即该节点中的元素个数是否等于M，如果小于则满足
- 如果插入后节点不满足B树的性质，需要对该节点进行分裂：申请新节点，找到该节点的中间位置，将该节点中间位置右侧的元素以及其孩子搬移到新节点中，将中间位置元素以及新节点往该节点的双亲节点中插入，即继续4
- 如果向上已经分裂到根节点的位置，插入结束
B树的验证
跑一个中序，如果出来时有序序列，说明B树是合法的
思路很简单：在访问节点之前，先递归访问它的左子树。
void _InOrder(Node* cur)
{
if (cur == nullptr)
return;
// 左 根 左 根 ... 右
size_t i = 0;
for (; i < cur->_n; ++i)
{
_InOrder(cur->_subs[i]); // 左子树
cout << cur->_keys[i] << " "; // 根
}
_InOrder(cur->_subs[i]); // 最后的那个右子树
}
void InOrder()
{
_InOrder(_root);
}BTree.h实现代码
#pragma once
#include<map>
#include<iostream>
using namespace std;
#pragma once
template<class K, size_t M>
struct BTreeNode
{
//K _keys[M - 1];
//BTreeNode<K, M>* _subs[M];
// 为了方便插入以后再分裂，多给一个空间
K _keys[M];
BTreeNode<K, M>* _subs[M + 1];
BTreeNode<K, M>* _parent;
size_t _n; // 记录实际存储多个关键字
BTreeNode()
{
for (size_t i = 0; i < M; ++i)
{
_keys[i] = K();
_subs[i] = nullptr;
}
_subs[M] = nullptr;
_parent = nullptr;
_n = 0;
}
};
// 数据是存在磁盘，K是磁盘地址
template<class K, size_t M>
class BTree
{
typedef BTreeNode<K, M> Node;
public:
pair<Node*, int> Find(const K& key)
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
// 在一个节点查找
size_t i = 0;
while (i < cur->_n)
{
if (key < cur->_keys[i])
{
break;
}
else if (key > cur->_keys[i])
{
++i;
}
else
{
return make_pair(cur, i);
}
}
// 往孩子去跳
parent = cur;
cur = cur->_subs[i];
}
return make_pair(parent, -1);
}
void InsertKey(Node* node, const K& key, Node* child)
{
int end = node->_n - 1;
while (end >= 0)
{
if (key < node->_keys[end])
{
// 挪动key和他的右孩子
node->_keys[end + 1] = node->_keys[end];
node->_subs[end + 2] = node->_subs[end + 1];
--end;
}
else
{
break;
}
}
node->_keys[end + 1] = key;
node->_subs[end + 2] = child;
if (child)
{
child->_parent = node;
}
node->_n++;
}
bool Insert(const K& key)
{
if (_root == nullptr)
{
_root = new Node;
_root->_keys[0] = key;
_root->_n++;
return true;
}
// key已经存在，不允许插入
pair<Node*, int> ret = Find(key);
if (ret.second >= 0)
{
return false;
}
// 如果没有找到，find顺便带回了要插入的那个叶子节点
// 循环每次往cur插入 newkey和child
Node* parent = ret.first;
K newKey = key;
Node* child = nullptr;
while (1)
{
InsertKey(parent, newKey, child);
// 满了就要分裂
// 没有满，插入就结束
if (parent->_n < M)
{
return true;
}
else
{
size_t mid = M / 2;
// 分裂一半[mid+1, M-1]给兄弟
Node* brother = new Node;
size_t j = 0;
size_t i = mid + 1;
for (; i <= M - 1; ++i)
{
// 分裂拷贝key和key的左孩子
brother->_keys[j] = parent->_keys[i];
brother->_subs[j] = parent->_subs[i];
if (parent->_subs[i])
{
parent->_subs[i]->_parent = brother;
}
++j;
// 拷走重置一下方便观察
parent->_keys[i] = K();
parent->_subs[i] = nullptr;
}
// 还有最后一个右孩子拷给
brother->_subs[j] = parent->_subs[i];
if (parent->_subs[i])
{
parent->_subs[i]->_parent = brother;
}
parent->_subs[i] = nullptr;
brother->_n = j;
parent->_n -= (brother->_n + 1);
K midKey = parent->_keys[mid];
parent->_keys[mid] = K();
// 说明刚刚分裂是根节点
if (parent->_parent == nullptr)
{
_root = new Node;
_root->_keys[0] = midKey;
_root->_subs[0] = parent;
_root->_subs[1] = brother;
_root->_n = 1;
parent->_parent = _root;
brother->_parent = _root;
break;
}
else
{
// 转换成往parent->parent 去插入parent->[mid] 和 brother
newKey = midKey;
child = brother;
parent = parent->_parent;
}
}
}
return true;
}
void _InOrder(Node* cur)
{
if (cur == nullptr)
return;
// 左 根 左 根 ... 右
size_t i = 0;
for (; i < cur->_n; ++i)
{
_InOrder(cur->_subs[i]); // 左子树
cout << cur->_keys[i] << " "; // 根
}
_InOrder(cur->_subs[i]); // 最后的那个右子树
}
void InOrder()
{
_InOrder(_root);
}
private:
Node* _root = nullptr;
};
void TestBtree()
{
int a[] = { 53, 139, 75, 49, 145, 36, 101 };
BTree<int, 3> t;
for (auto e : a)
{
t.Insert(e);
}
t.InOrder();
}B+树
B+树是B树的变形，是在B树基础上优化的多路平衡搜索树，B+树的规则跟B树基本类似，但是又
在B树的基础上做了以下几点改进优化：
- 分支节点的子树指针与关键字个数相同
- 分支节点的子树指针p[i]指向关键字值大小在[k[i]，k[i+1])区间之间
- 所有叶子节点增加一个链接指针链接在一起
- 所有关键字及其映射数据都在叶子节点出现
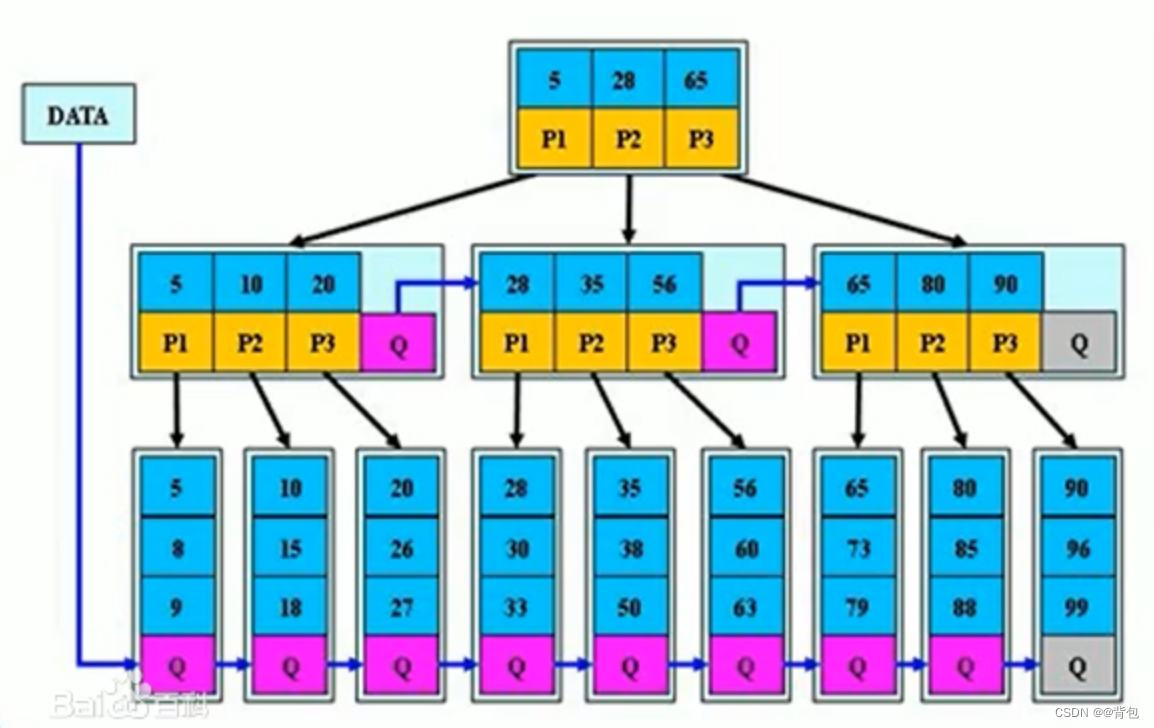
这个就是一棵B+树 ，它的一个节点中的key数量和孩子数量是一样的。
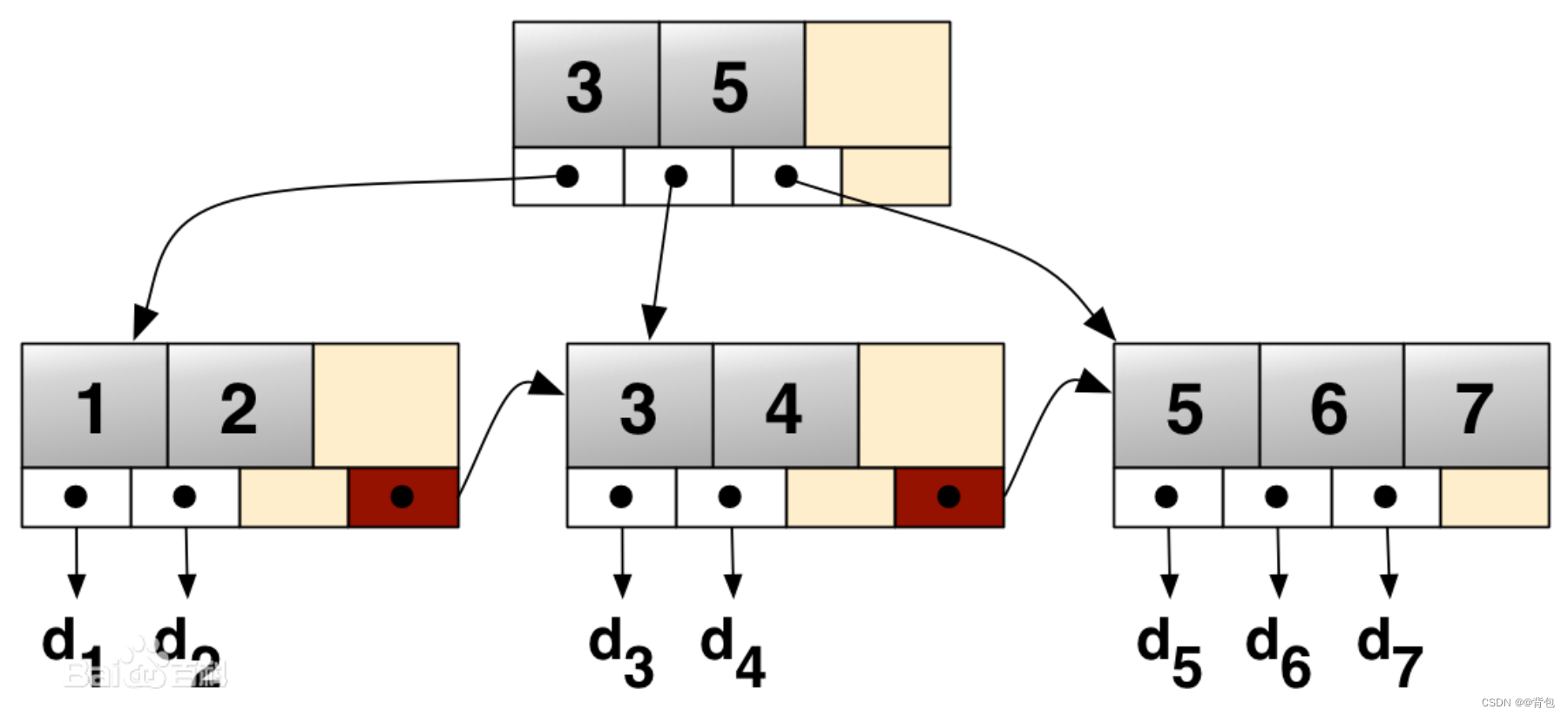
B+树的插入
同样，博主也通过画图的方式带着大家理解B+树，这样更便于我们的理解。
我们通过序列[53,49,75,139,49,145,36,150,155]来理解3阶B+树的插入
同样，三阶B+树，每层节点我们开4个空间
- 插入53，49，75
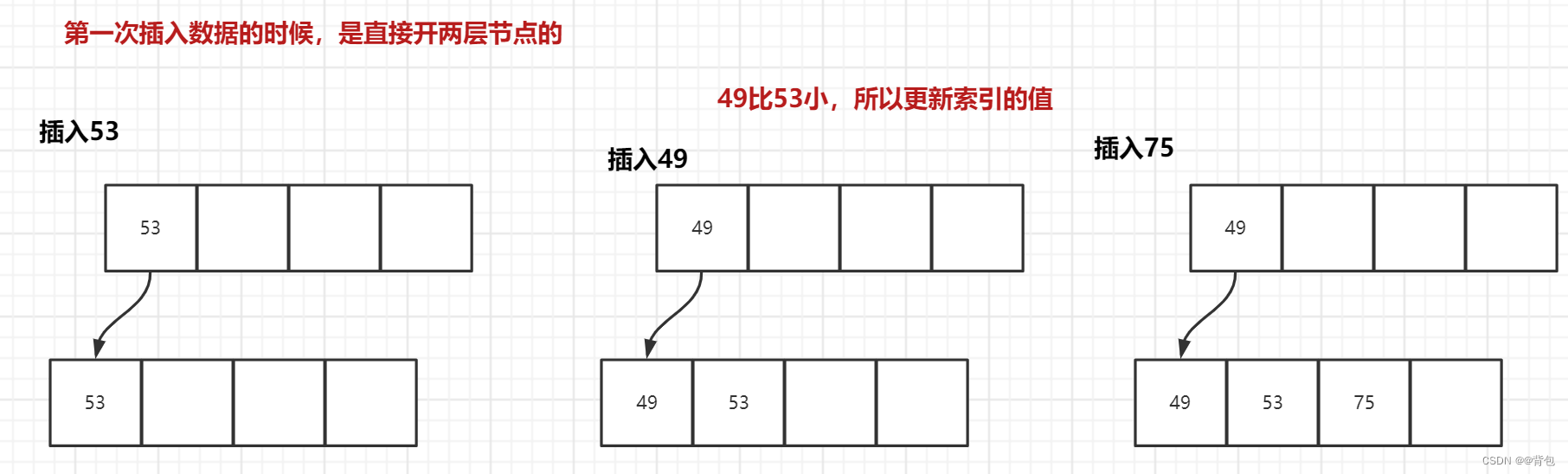
- 插入139
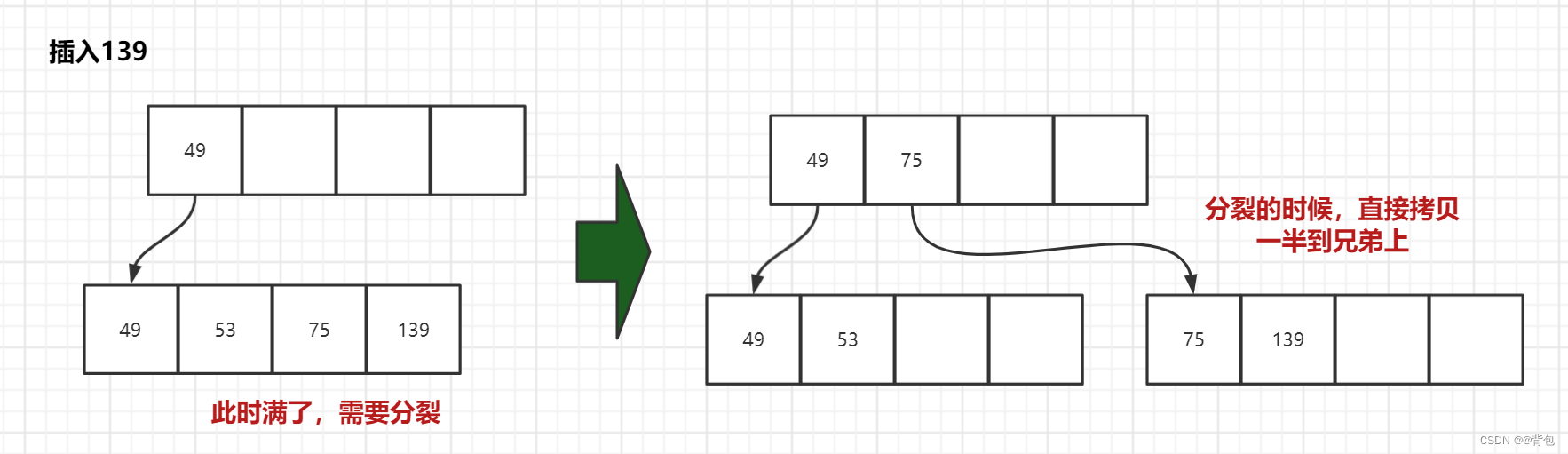
- 插入36
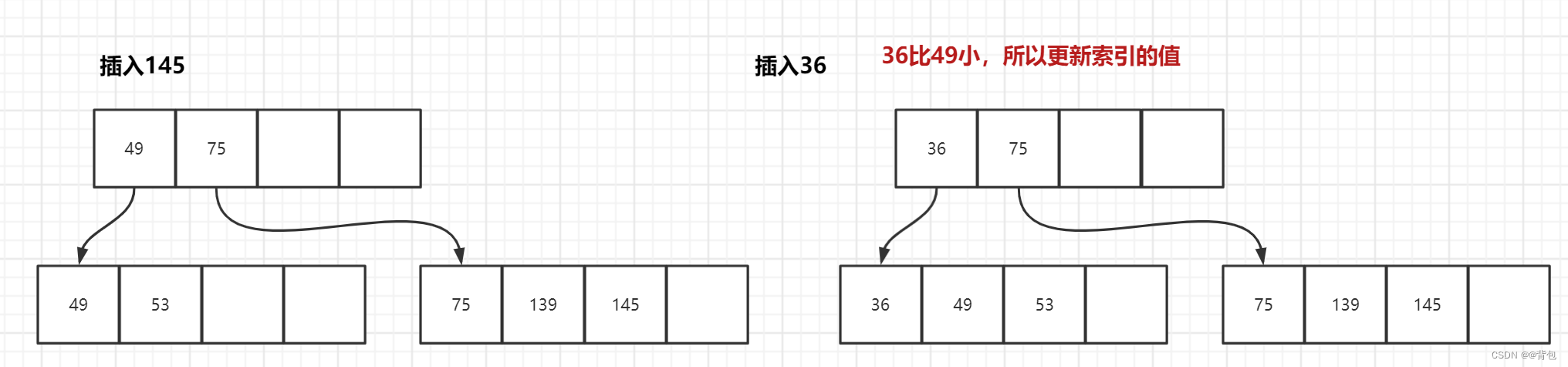
- 插入101
- 插入150，155
此时就需要一个连续的分裂过程了
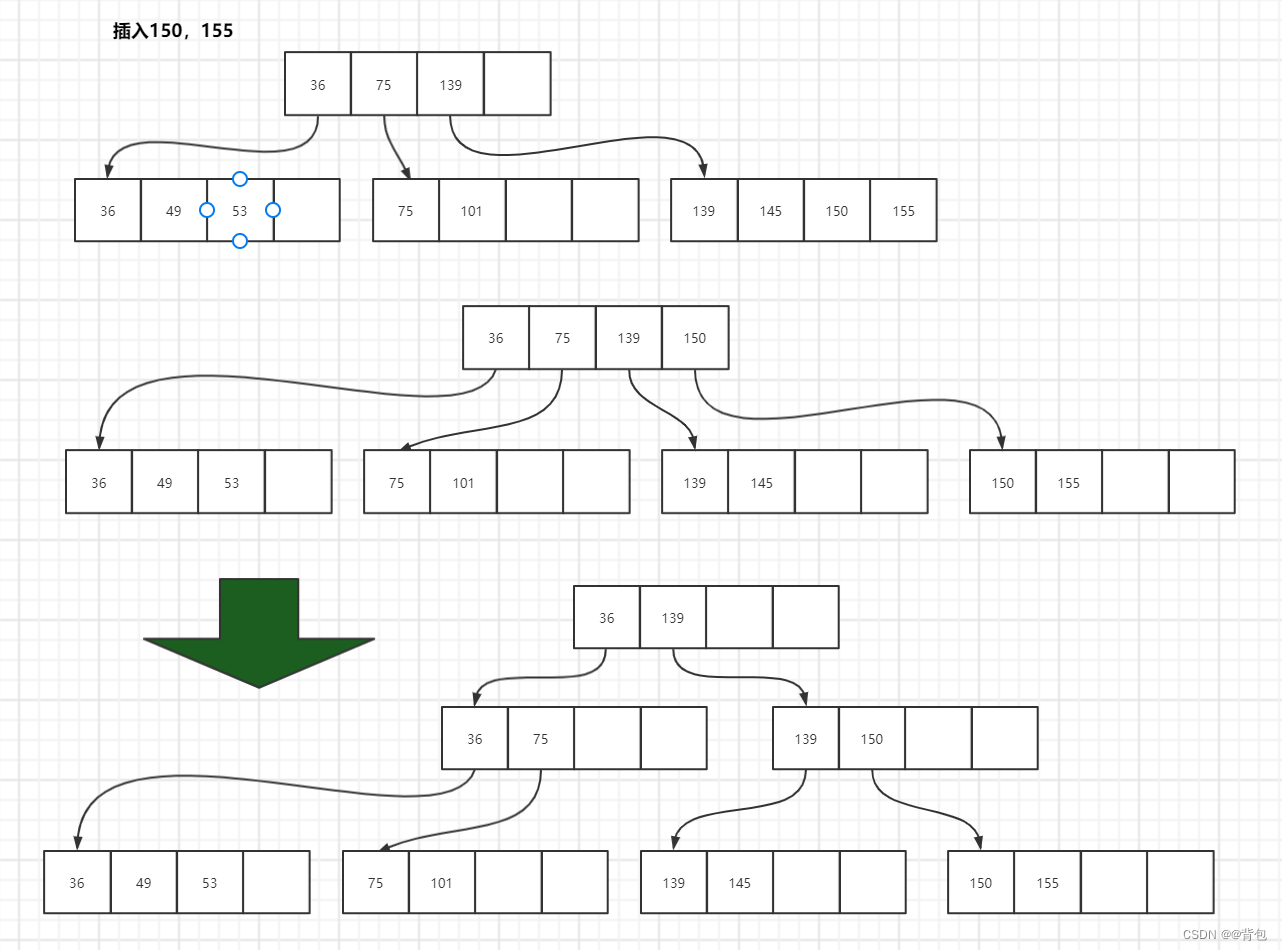
看到这里，相信大家已经对B+树是如何完成插入，有了一定的了解了。
B+树的性质
B+树的特性：
- 所有关键字都出现在叶子节点的链表中，且链表中的节点都是有序的。
- 不可能在分支节点中命中。
- 分支节点相当于是叶子节点的索引，叶子节点才是存储数据的数据层。
B*树
B*树是B+树的变形，在B+树的非根和非叶子节点再增加指向兄弟节点的指针。
B+树的分裂：
当一个结点满时，分配一个新的结点，并将原结点中1/2的数据复制到新结点，最后在父结点中增
加新结点的指针；B+树的分裂只影响原结点和父结点，而不会影响兄弟结点，所以它不需要指向
兄弟的指针。
B*树的分裂：
当一个结点满时，如果它的下一个兄弟结点未满，那么将一部分数据移到兄弟结点中，再在原结
点插入关键字，最后修改父结点中兄弟结点的关键字（因为兄弟结点的关键字范围改变了）；如
果兄弟也满了，则在原结点与兄弟结点之间增加新结点，并各复制1/3的数据到新结点，最后在父
结点增加新结点的指针。
所以，B*树分配新结点的概率比B+树要低，空间使用率更高；
B树系列结构总结
通过以上介绍，大致将B树，B+树，B*树总结如下：
B树：有序数组+平衡多叉树；
B+树：有序数组链表+平衡多叉树；
B*树：一棵更丰满的，空间利用率更高的B+树。
B树系列性能总结
在内存中做内查找:
B树系列和哈希和平衡搜索树对比:
单纯论树的高度，搜索效率而言，B树确实不错但是B树系列有一些隐形坏处:
- 空间利用率低，消耗高
- 插入删除数据时，分裂和合并节点，那么必然挪动数据3.虽然高度耕地，但是在内存中而言，和哈希和平衡搜索树还是一个量级的结论:实质上B树系列在内存中体现不出优势!
因此，B树的优势主要体现在，外查找中！
B树系列的应用
B-树最常见的应用就是用来做索引。索引通俗的说就是为了方便用户快速找到所寻之物，比如：
书籍目录可以让读者快速找到相关信息，hao123网页导航网站，为了让用户能够快速的找到有价
值的分类网站，本质上就是互联网页面中的索引结构。
MySQL官方对索引的定义为：索引(index)是帮助MySQL高效获取数据的数据结构，简单来说：
索引就是数据结构。
当数据量很大时，为了能够方便管理数据，提高数据查询的效率，一般都会选择将数据保存到数
据库，因此数据库不仅仅是帮助用户管理数据，而且数据库系统还维护着满足特定查找算法的数
据结构，这些数据结构以某种方式引用数据，这样就可以在这些数据结构上实现高级查找算法，
该数据结构就是索引。
总结
看到这里,大家应该对B树系列有了比较深入的了解了。这篇博客博主花了很多心思在画图上，也投入了很多时间到画图上。希望大家可以多多支持，一键三连，点赞关注收藏评论后在离开哦!
( 转载时请注明作者和出处。未经许可，请勿用于商业用途 )
更多文章请访问我的主页
@背包https://blog.csdn.net/Yu_Cblog?type=blog
![[附源码]Node.js计算机毕业设计工资管理系统PPTExpress](https://img-blog.csdnimg.cn/c1562d7f87424eab9b0f64cb9c5b488e.png)