🧸🧸🧸各位大佬大家好，我是猪皮兄弟🧸🧸🧸

一、搜索二叉树框架

	template<class K>
	struct BSTreeNode
	{
		BSTreeNode<K>* _left;
		BSTreeNode<K>* _right;
		K _key;
		BSTreeNode(const K& key)
			:_key(key)
			, _left(nullptr)
			, _right(nullptr)
		{}

	};

	template<class K>//key
	class BSTree
	{
		typedef BSTreeNode<K> Node;
		//...
		Node* _root = nullptr;
	};

二、搜索二叉树概念

搜索二叉树又称二叉搜索树，或者是一颗空树，或者是具有以下性质的二叉树
①若它的左子树不为空，则左子树上所有结点的值都小于根结点
②若它的右子树不为空，则右子树上所有结点的值都大于根结点
③它的左右子树，也分别是搜索二叉树

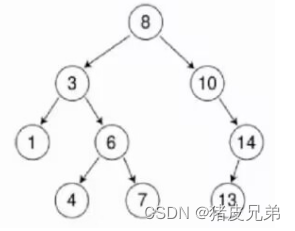
也就是找小往左边走，找大往右边走，二叉搜索树最大的价值就是用于搜索，搜索二叉树最多查找高度次，因为搜索二叉树中序遍历就是已排序的数列，所以也叫二叉排序树，如上图的中序遍历结果 1 3 4 6 7 8 10 13 14
另外，搜索二叉树是不能有相同键值的，遇到相同键值不存储，搜索二叉树除了搜索外，顺带的功能就是排序+去重

中序遍历：

//...
public:
void InOrder()
{
	InOrder(_root);
}
private:
void InOrder(Node*root)
{
	if(root->left ==nullptr) return;
	InOrder(root->left);
	cout<<root->_key<<" ";
	InOrder(root->right);
}

三、搜索二叉树操作

普通的插入删除查找等等我就不写了

①Erase

删除结点只有一个孩子的话直接交给父节点即可，比如上面删除14，直接给10这种情况有一个特例，就是删除根的时候，只有一个孩子的话，直接将root转移给孩子即可

但是当该结点有两个孩子呢？比如删除上面的6
这种情况需要用到替换法，替换有两种方式，因为搜索二叉树的左<根<右
所以
①找到该节点左子树的最右，也就是最大结点进行替换，要保证搜索二叉树的特性
②找到该节点右子树的最左，也就是 最小结点进行替换

//Erase代码
bool Erase(const K&key)
{
	Node*cur = _root;//根
	Node*parent = cur;
	while(cur)
	{
		if(cur->val<key)
		{
			cur=cur->_right;
			parent = cur;
		}
		else if(cur->val>key)
		{	
			cur=cur->_left;
			parent = cur;
		}
		else
		{
			//三种情况
			//一个孩子&&根   一个孩子&&非根   两个孩子
			if(cur->_left ==nullptr)
			{
				if(cur==_root)
				{	//_root转移
					_root = cur->_right;
				}
				else
				{
					if(cur==parent->_left)
					{
						parent->_left = cur->_right;
					}
					else
					{
						parent->_right = cur->_right;
					}
					//需要找父节点，所以提前找好
					delete cur;
					cur=nullptr;//习惯
				}
			}
			else if(cur->_right==nullptr)
			{
					if(cur==_root)
					{	//_root转移
						_root = cur->_left;
					}
					else
					{
						if(cur==parent->_left)
						{
							parent->_left = cur->_left;
						}
						else
						{
							parent->_right = cur->_left;
						}
						//需要找父节点，所以提前找好
						delete cur;
						cur=nullptr;//习惯
					}
				}
			else//两个孩子
			{
				//我们选择右子树的最小进行替换
				Node*find_min = cur->right;
				while(find_min->_left)
				{
					find_min = find_min->_left;
				}
				cur->_key = find_min->_key;//cur就是要替换的位置
				delte find_min;
				find_min=nullptr;//这个必须，不然是野指针
			}
			return true;
		}
		return false;
	}
}

②Find递归

public:
//...
bool FindR(const K&key)
{
	return _FindR(_root,key);
}
private:
bool  _FindR(Node*root,const K&key)
{
	if(root==nullptr) return false;
	if(root->val==key) return true;
	else if(root->_key<key)
		return _FindR(root->_right,key);
	else
		return _FindR(root->_left,key);
}

③Insert递归

public:
//...
bool InsertR(const K&key)
{
	return _InsertR(_root,key);
}
private:
bool  _InsertR(Node*root,const K&key)
{
	if(root==nullptr)
	{	
		root = new Node(key);//构造函数缺省左右nullptr
		return true;
	}
	if(root->_key<key)
		return InsertR(root->right,key);
	else if(root->_key>key)
		return InsertR(root->left,key);
	else return false;
}

④Erase递归，比Erase更简洁

public:
//...
bool EraseR(const K&key)
{
	return _EraseR(_root,key);
}
private:
bool  _EraseR(Node*root,const K&key)
{
	if(root==nullptr) return false;
	if(root->_key<key)
	{
		return _EraseR(root->_right,key);
	}
	else if(root->_key>key)
	{
		return _EraseR(root->_left,key);
	}
	else 
	{
		Node*del = root;//需要delete的结点
		if(root->_left == nullptr)
		{
			root=root->_right;//被取代
			delete del;
		}
		else if(root->_right ==nullptr)
		{
			root=root->left;
			delete del;//被子树取代
		}
		else
		{//两个孩子
			//用右子树最小来替换
			Node*find_mind=root->right;
			while(find_min->_left)
			{
				find-min=find_min ->_left;
			}
			swap(root->_key,find_min_key);
			//换到右子树的最后，然后再去Erase它就可以了
			_EraseR(_root->right,key);
		}
		return true;
	}
}

将要删的结点交换到右子树的最小值位置，再去delete

⑤析构函数

因为析构函数无法给参数，所以让析构函数调用Destory进行一个递归的删除

public:
~BSTree()
{
	Destory(_root);
}
private:
void Destory(Node*root)
{
	if(root==nullptr)
	{
		return;
	}
	Destory(root->left);
	Destory(root->right);
	delete root;
	//后序遍历来delete
}

⑥搜索二叉树的拷贝

二叉搜索树的构造需要用后序遍历来构造，需要保证根结点最后被构造才行

BSTree(const BSTree&bst)
{
	_root= _Copy(bst._root);
	//可以访问同类对象的私有成员
}
Node*_Copy(Node*root)
{
	if(root==nullptr)
	{
		return nullptr;
	}
	Node*copyRoot = new Node(root->_key);
	copyRoot->_left=_Copy(root->_left);
    copyRoot->_right=_Copy(root->_right);
    return copyRoot;//后序遍历
}

因为拷贝构造也是构造函数，拷贝构造只是构造函数的一种重载形式，所以，如果写了拷贝构造的话，编译器是不会默认生成默认构造的，需要自己去写。
或者呢，就要用一个关键字BSTree() = defualt;表示让编译器强制生成默认的构造函数

⑦赋值运算符重载

BSTree<K> &operator=(BSTree<K> bst)
{
	swap(bast._root,_root);
	return *this;
}

bst是传值传参，通过对拷贝构造的复用生成bst
然后此时只需要swap即可，因为我之前的旧树出作用域的时候会被自动析构，不用管

四、搜索二叉树存在的问题

搜索二叉树增删查的时间复杂度是O(h) h是树的高度
最坏的单支情况下是O(N)，所以说搜索二叉树还是有缺陷的，最坏情况下增删查太慢了，想达到O(logN必须是满二叉树或者完全二叉树)，所以就有了AVL树，红黑树等等，这些平衡树和搜索树的却别仅仅在效率上，功能上并没有区别