快速排序也是从冒泡排序演化而来
使用了 分治法（快的原因）

快速排序和冒泡排序共同点：通过元素之间的比较和交换位置来达到排序的目的。
快速排序和冒泡排序不同点：冒泡排序在每一轮中只把1个元素冒泡到数列的一端，而快速排序则
在每一轮挑选一个基准元素，并让其他比它大的元素移动到数列一边，比它小的元素移动到数列的另一边，从而把数列拆解成两个部分（分治法）

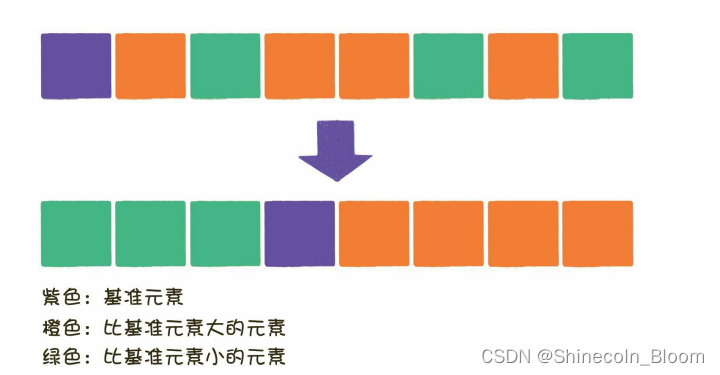
分治法思想

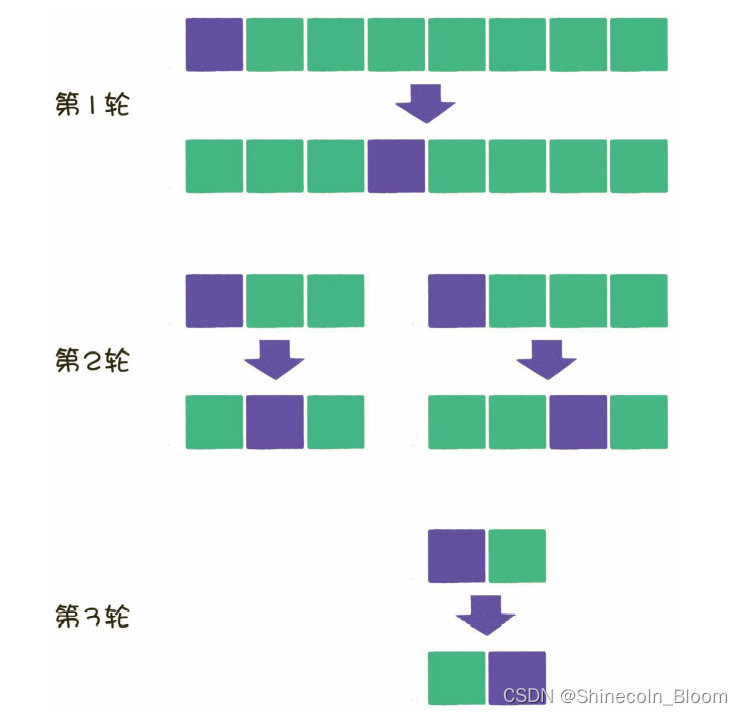
在分治法的思想下，原数列在每一轮都被拆分成两部分，每一部分在下一轮又分别被拆分成两部分，直到不可再分为止。

快速排序算法总体的平均时间复杂度是O(nlogn)。

基准元素的选择，以及元素的交换，都是快速排序的核心问题。

基准元素的选择

随机选择一个元素作为基准元素，并且让基准元素和数列首元素交换位置。
原理：这样一来，即使在数列完全逆序的情况下，也可以有效地将数列分成两部分。

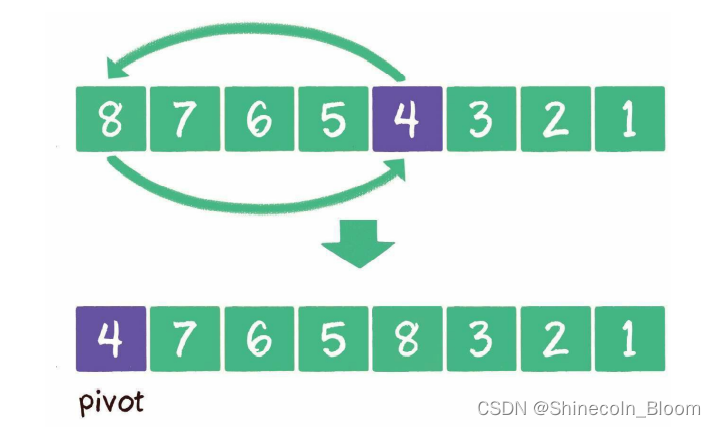
当然，即使是随机选择基准元素，也会有极小的几率选到数列的最大值或最小值，同样会影响分治的效果。
所以，虽然快速排序的平均时间复杂度是O(nlogn)，但最坏情况下的时间复杂度是O(n²)。

元素交换

选定了基准元素以后，我们要做的就是把其他元素中小于基准元素的都交换到基准元素一边，大于基准元素的都交换到基准元素另一边。

1. 双边循环法
2. 单边循环法

双边循环法

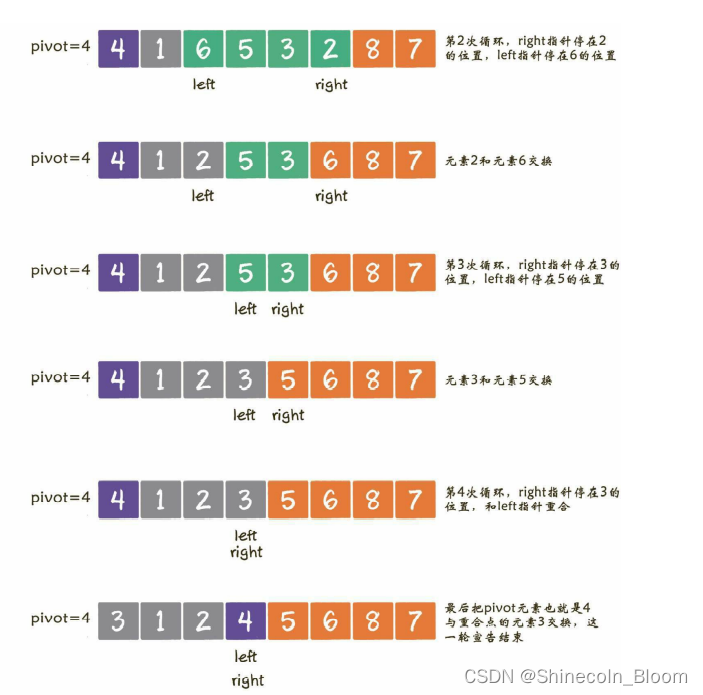
就是left指针指向的元素逐次和基准元素pivot比较，right指针指向的元素逐次和基准元素pivot比较。

具体流程为：从right指针开始，让指针所指向的元素和基准元素做比较。如果大于或等于pivot，则指针向左移动；如果小于pivot，则right指针停止移动，切换到left指针。轮到left指针行动，让指针所指向的元素和基准元素做比较。如果小于或等于
pivot，则指针向右移动；如果大于pivot，则left指针停止移动。
最后：让left和right指针所指向的元素进行交换。


具体过程如下：

JAVA实现

省去了随机选择基准元素的过程，直接把首元素作为基准元素

package mysort.quickSorting;

public class quickSorting {


    /**
     *
     * @param arr    待交换的数组
     * @param startIndex  起始下标
     * @param endIndex    结束下标
     * @return
     */
    private static int partition(int[]arr ,int startIndex,int endIndex){
        // 取第1个位置（也可以选择随机位置）的元素作为基准元素
        int pivot = arr[startIndex];
        int left = startIndex;
        int right = endIndex;

        while (left!=right){
            //控制right 指针比较并左移
            while (left<right&&arr[right]>pivot){
                right--;
            }
            //控制left指针比较并右移
            //有等于是因为：int pivot = arr[startIndex]; int left = startIndex;
            while (left<right&&arr[left]<=pivot){
                left++;
            }
            //left和right都找到后，交换这俩的值
            if (left<right){
                int p =arr[left];
                arr[left]=arr[right];
                arr[right]=p;
            }
        }
        //到这一步的时候left==right了
        //执行pivot 和指针重合点交换
        arr[startIndex] = arr[left];
        arr[left] = pivot;
        //至此，依据第一个元素（基准元素pivot），把数组大于第一个元素的放在他右边，小于的放在左边，并返回基准元素（pivot）最终的下标
        return left;
    }

    public static void quickSort(int []arr,int startIndex,int endIndex){
        //递归出口：startIndex大于或等于endIndex时
        //也就是分的不能再分的时候startIndex==endIndex
        if(startIndex>=endIndex){
            return;
        }
        //选取第一个元素为基准元素，把数组排序后，返回基准元素的位置
        int pivotIndex = partition(arr,startIndex,endIndex);
        //在根据基准元素，把数组划分为俩部分（分治法）,对俩个子部分分别执行快排
        quickSort(arr,startIndex,pivotIndex-1);
        quickSort(arr,pivotIndex+1,endIndex);
    }
}

其中：quickSort方法通过递归的方式，实现了分而治之的思想。（把大问题划分为一个一个的小问题）
partition方法则实现了元素的交换，让数列中的元素依据自身大小，分别交换到基准元素的左右两边。

单边循环法

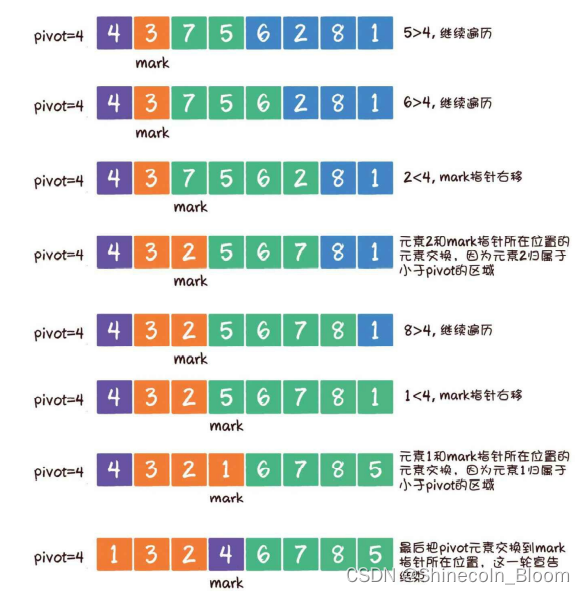
首先选定基准元素pivot。同时，设置一个mark指针指向数列起始位置，这个mark指针代表小于基准元素的区域边界。

如果遍历到的元素大于基准元素，就继续往后遍历。

如果遍历到的元素小于基准元素，则需要做两件事：第一，把mark指针右移1位，因为小于pivot的区域边界增大了1；第二，让最新遍历到的元素和mark指针所在位置的元素交换位置，因为最新遍历的元素归属于小于pivot的区域。

蓝色表示当前遍历的位置
遍历到元素7，7>4，所以继续遍历。mark指针不动

遍历到的元素是3，3<4，所以mark指针右移1位。让元素3和mark指针所在位置的元素交换，因为元素3归属于小于pivot
的区域。


之后的步骤为：

其中分治都是递归实现的，区别就在于：双边循环法和单边循环法的区别在于partition函数的实现

JAVA实现

package mysort.quickSorting;

import java.util.Arrays;

//都是从小到大排序（左-->右）
public class quickSorting2 {

    /**
     * 单边循环法
     * @param arr         待交换的数组
     * @param startIndex  起始下标
     * @param endIndex    结束下标
     * @return
     */
    private static int partition(int[]arr,int startIndex,int endIndex){
        // 取第1个位置（也可以选择随机位置）的元素作为基准元素
        int pivot = arr[startIndex];
        //mark指针代表小于基准元素的区域边界
        int mark = startIndex;

        for (int i = startIndex+1;i<=endIndex;i++){
            //如果当前元素比 基准元素 小
            if(arr[i]<pivot){
                //小于基准元素的区域边界扩张一个单位
                mark++;
                //让最新遍历到的元素和mark指针所在位置的元素交换位置
                int p = arr[mark];
                arr[mark] = arr[i];
                arr[i] = p;
            }
        }
        //遍历结束后，把基准元素(pivot)放到相应的位置去(mask位置)
        arr[startIndex] = arr[mark];
        arr[mark] = pivot;
        //最后返回基准元素下标，为下一步分治提供划分的依据
        return mark;
    }

    public static void quickSort(int[]arr,int startIndex,int endIndex){
        //递归出口
        //也就是分治法划分的不能再划分的最小单位
        if(startIndex>=endIndex){
            return;
        }
        //得到基准元素位置
        int pivotIndex = partition(arr,startIndex,endIndex);
        //根据基准元素，分成两部分进行递归排序（分治法）
        quickSort(arr,startIndex,pivotIndex-1);
        quickSort(arr,pivotIndex+1,endIndex);
    }

    public static void main(String[] args) {
        int[]arr = new int[]{4,4,6,5,3,2,8,1};
        quickSort(arr,0,arr.length-1);
        System.out.println(Arrays.toString(arr));
    }
}

快速排序实现方法，都是以递归为基础的。其实快速排序也可以基于非递归的方式来实现。（栈）
绝大多数的递归逻辑，都可以用栈的方式来代替
每次进入一个新方法，就相当于入栈；每次有方法返回，就相当于出栈。