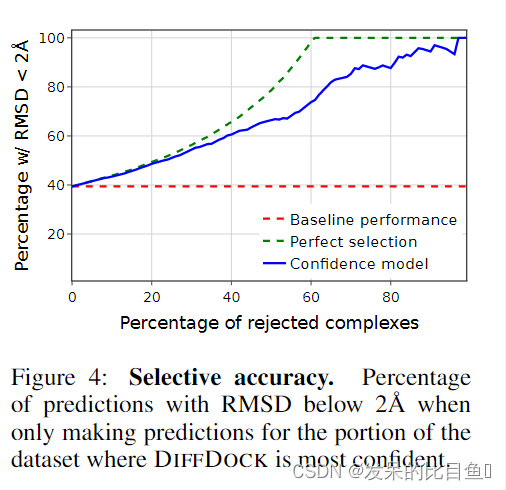
本文内容借鉴一本我非常喜欢的书——《数据结构与算法图解》。学习之余,我决定把这本书精彩的部分摘录出来与大家分享。
写在前面
从之前的章节中我们了解到,影响算法性能的主要因素是其所需的步数。
然而,我们不能简单地把一个算法记为“22步算法”,把另一个算法记为“400步算法”,因为一个算法的步数并不是固定的。
以线性查找为例,它的步数等于数组的元素数量。如果数组有22个元素,线性查找就需要 22步;如果数组有 400个元素,线性查找就需要 400步。
量化线性查找效率的更准确的方式应该是:对于具有 N 个元素的数组,线性查找最多需要 N步。
为了方便表达数据结构和算法的时间复杂度,计算机科学家从数学界借鉴了一种简洁又通用的方式,那就是大 O 记法。
掌握了大 O记法,就掌握了算法分析的专业工具。
1.大O:数步数
为了统一描述,大 O不关注算法所用的时间,只关注其所用的步数。
第 1章介绍过,数组不论多大,读取都只需 1步。用大 O记法来表示,就是:O(1)
O(1)意味着一种算法无论面对多大的数据量,其步数总是相同的。
就像无论数组有多大,读取元素都只要 1 步。这 1 步在旧机器上也许要花 20 分钟,而用现代的硬件却只要 1 纳秒。但这两种情况下,读取数组都是 1步。其他也属于 O(1)的操作还包括数组末尾的插入与删除。之前已证明,无论数组有多大,这两种操作都只需 1步,所以它们的效率都是O(1)。
下面研究一下大 O 记法如何描述线性查找的效率。回想一下,线性查找在数组上要逐个检查每个格子。在最坏情况下,线性查找所需的步数等于格子数。即如前所述:对于 N个元素的数组,线性查找需要花 N步。
用大 O记法来表示,即为:O(N)
2.常数时间与线性时间
从 O(N)可以看出,大 O 记法不只是用固定的数字(如 22、440)来表示算法的步数,而是基于要处理的数据量来描述算法所需的步数。
或者说,大 O 解答的是这样的问题:当数据增长时,步数如何变化?
O(N)算法所需的步数等于数据量,意思是当数组增加一个元素时,O(N)算法就要增加 1步。而 O(1)算法无论面对多大的数组,其步数都不变。
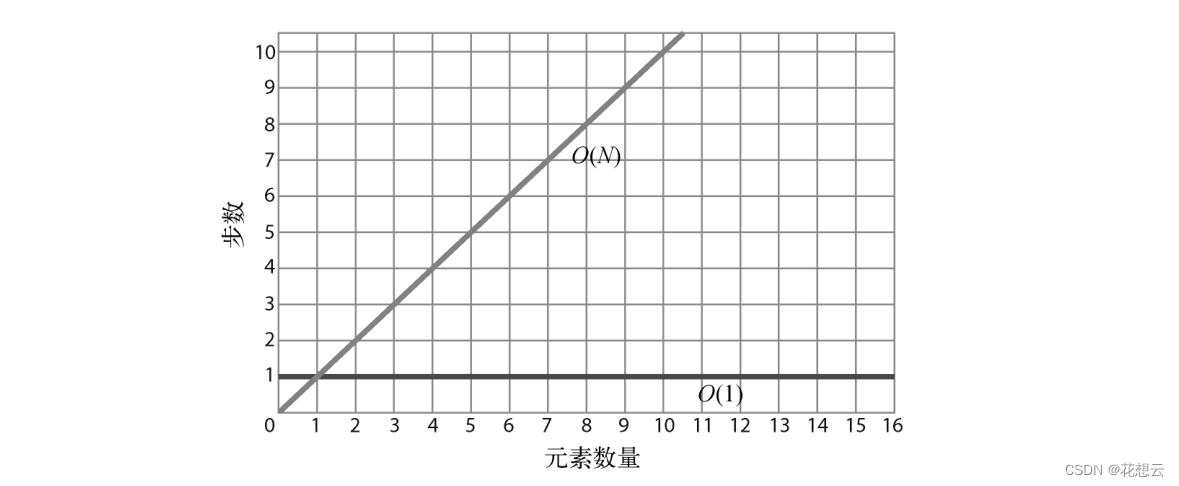
当数据增加一个单位时,算法也随之增加一步。也就是说,数据越多,算法所需的步数就越多。O(N)也被称为线性时间。
相比之下,O(1)则为一条水平线,因为不管数据量是多少,算法的步数都恒定。所以,O(1)也被称为为常数时间。
因为大 O主要关注的是数据量变动时算法的性能变化,所以,即使一个算法的恒定步数不是 1,它也可以被归类为 O(1)。

O(1)永远比O(N)更高效,原因在于,当元素数量无限增多时,O(N)总会在某一临界值超过O(1)。
3.同一算法,不同场景
之前的章节我们提到,线性查找并不总是 O(N)的。当要找的元素在数组末尾,那确实是 O(N)。但如果它在数组开头,1步就能找到的话,那么技术上来说应该是 O(1)。所以概括来说,线性查找的最好情况是 O(1),最坏情况是 O(N)。
虽然大 O 可以用来表示给定算法的最好和最坏的情景,但若无特别说明,大 O 记法一般都是指最坏情况。
这种悲观主义其实是很有用的:知道各种算法会差到什么程度,能使我们做好最坏打算,以选出最适合的算法。
4.第三种算法
上一章我们学到:在同一个有序数组里,二分查找比线性查找要快。
算法为何重要(二分查找)![]() http://t.csdn.cn/YPs4s下面就来看看如何用大O记法描述二分查找。
http://t.csdn.cn/YPs4s下面就来看看如何用大O记法描述二分查找。
二分查找的大 O记法是:O(log N)
简单分析一下,倘若要用二分查找在含有N个元素的有序数组中查找某个元素。
二分查找的基本思想是,每次我们都能排除掉一半的数据。
所以考虑最坏情况,就是数组里没有我们要查找的元素,那么我们每次排除一半的元素,多
少次才能全部排除(或者说只剩一个元素)呢?
答案是
。
简单来说,O(log N)意味着该算法当数据量翻倍时,步数加 1。
这里我们所提过的 3种时间复杂度,按照效率由高到低来排序的话,会是这样:
O(1)<O(log N)<O(N)

现在回到大 O记法。当我们说 O(log N)时,其实指的是 O(log 2 N),不过为了方便就省略了2而已。简单来说,O(log N)算法的步数等于二分数据直至元素剩余 1 个的次数。
下表是 O(N)和 O(log N)的效率对比。

每次数据量翻倍时,O(N)算法的步数也跟着翻倍,O(log N)算法却只需加 1。
总结
学会大 O记法,我们在比较算法时就有了一致的参考系。有了它,我们就可以在现实场景中测量各种数据结构和算法,写出更快的代码,更轻松地应对高负荷的环境。
下一章会用一个实际的例子,让你看到大 O记法如何帮助我们显著地提高代码的性能。